Imandra CodeLogician: Neuro-Symbolic Reasoning for Precise Analysis of Software Logic

Large Language Models (LLMs) have shown strong performance on code understanding tasks, yet they fundamentally lack the ability to perform precise, exhaustive mathematical reasoning about program behavior. Existing benchmarks either focus on mathematical proof automation, largely disconnected from real-world software, or on engineering tasks that do not require semantic rigor. We present CodeLogician, a neurosymbolic agent for precise analysis of software logic, integrated with ImandraX, an industrial automated reasoning engine deployed in financial markets and safety-critical systems. Unlike prior approaches that use formal methods primarily to validate LLM outputs, CodeLogician uses LLMs to construct explicit formal models of software systems, enabling automated reasoning to answer rich semantic questions beyond binary verification outcomes. To rigorously evaluate mathematical reasoning about software logic, we introduce code-logic-bench, a benchmark targeting the middle ground between theorem proving and software engineering benchmarks. It measures reasoning correctness about program state spaces, control flow, coverage constraints, and edge cases, with ground truth defined via formal modeling and region decomposition. Comparing LLM-only reasoning against LLMs augmented with CodeLogician, formal augmentation yields substantial improvements, closing a 41-47 percentage point gap in reasoning accuracy. These results demonstrate that neurosymbolic integration is essential for scaling program analysis toward rigorous, autonomous software understanding.

Memoisation: Purely, Left-recursively, and with (Continuation Passing) Style

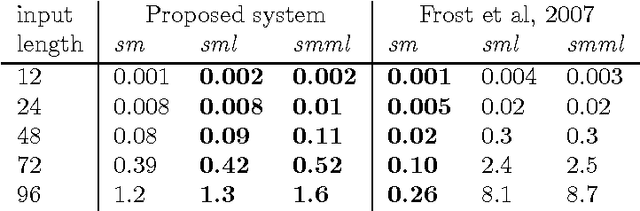
Memoisation, or tabling, is a well-known technique that yields large improvements in the performance of some recursive computations. Tabled resolution in Prologs such as XSB and B-Prolog can transform so called left-recursive predicates from non-terminating computations into finite and well-behaved ones. In the functional programming literature, memoisation has usually been implemented in a way that does not handle left-recursion, requiring supplementary mechanisms to prevent non-termination. A notable exception is Johnson's (1995) continuation passing approach in Scheme. This, however, relies on mutation of a memo table data structure and coding in explicit continuation passing style. We show how Johnson's approach can be implemented purely functionally in a modern, strongly typed functional language (OCaml), presented via a monadic interface that hides the implementation details, yet providing a way to return a compact represention of the memo tables at the end of the computation.