Imandra CodeLogician: Neuro-Symbolic Reasoning for Precise Analysis of Software Logic

Large Language Models (LLMs) have shown strong performance on code understanding tasks, yet they fundamentally lack the ability to perform precise, exhaustive mathematical reasoning about program behavior. Existing benchmarks either focus on mathematical proof automation, largely disconnected from real-world software, or on engineering tasks that do not require semantic rigor. We present CodeLogician, a neurosymbolic agent for precise analysis of software logic, integrated with ImandraX, an industrial automated reasoning engine deployed in financial markets and safety-critical systems. Unlike prior approaches that use formal methods primarily to validate LLM outputs, CodeLogician uses LLMs to construct explicit formal models of software systems, enabling automated reasoning to answer rich semantic questions beyond binary verification outcomes. To rigorously evaluate mathematical reasoning about software logic, we introduce code-logic-bench, a benchmark targeting the middle ground between theorem proving and software engineering benchmarks. It measures reasoning correctness about program state spaces, control flow, coverage constraints, and edge cases, with ground truth defined via formal modeling and region decomposition. Comparing LLM-only reasoning against LLMs augmented with CodeLogician, formal augmentation yields substantial improvements, closing a 41-47 percentage point gap in reasoning accuracy. These results demonstrate that neurosymbolic integration is essential for scaling program analysis toward rigorous, autonomous software understanding.

A Certified Proof Checker for Deep Neural Network Verification

Recent advances in the verification of deep neural networks (DNNs) have opened the way for broader usage of DNN verification technology in many application areas, including safety-critical ones. DNN verifiers are themselves complex programs that have been shown to be susceptible to errors and imprecisions; this in turn has raised the question of trust in DNN verifiers. One prominent attempt to address this issue is enhancing DNN verifiers with the capability of producing proofs of their results that are subject to independent algorithmic certification (proof checking). Formulations of proof production and proof checking already exist on top of the state-of-the-art Marabou DNN verifier. The native implementation of the proof checking algorithm for Marabou was done in C++ and itself raised the question of trust in the code (e.g., in the precision of floating point calculations or guarantees for implementation soundness). Here, we present an alternative implementation of the Marabou proof checking algorithm in Imandra -- an industrial functional programming language and prover -- that allows us to obtain an implementation with formal guarantees, including proofs of mathematical results underlying the algorithm, such as the use of the Farkas lemma.

Towards a Certified Proof Checker for Deep Neural Network Verification

Recent developments in deep neural networks (DNNs) have led to their adoption in safety-critical systems, which in turn has heightened the need for guaranteeing their safety. These safety properties of DNNs can be proven using tools developed by the verification community. However, these tools are themselves prone to implementation bugs and numerical stability problems, which make their reliability questionable. To overcome this, some verifiers produce proofs of their results which can be checked by a trusted checker. In this work, we present a novel implementation of a proof checker for DNN verification. It improves on existing implementations by offering numerical stability and greater verifiability. To achieve this, we leverage two key capabilities of Imandra, an industrial theorem prover: its support of infinite precision real arithmetic and its formal verification infrastructure. So far, we have implemented a proof checker in Imandra, specified its correctness properties and started to verify the checker's compliance with them. Our ongoing work focuses on completing the formal verification of the checker and further optimizing its performance.

Revisiting Variable Ordering for Real Quantifier Elimination using Machine Learning

Cylindrical Algebraic Decomposition (CAD) is a key proof technique for formal verification of cyber-physical systems. CAD is computationally expensive, with worst-case doubly-exponential complexity. Selecting an optimal variable ordering is paramount to efficient use of CAD. Prior work has demonstrated that machine learning can be useful in determining efficient variable orderings. Much of this work has been driven by CAD problems extracted from applications of the MetiTarski theorem prover. In this paper, we revisit this prior work and consider issues of bias in existing training and test data. We observe that the classical MetiTarski benchmarks are heavily biased towards particular variable orderings. To address this, we apply symmetries to create a new dataset containing more than 41K MetiTarski challenges designed to remove bias. Furthermore, we evaluate issues of information leakage, and test the generalizability of our models on the new dataset.

CheckINN: Wide Range Neural Network Verification in Imandra (Extended)

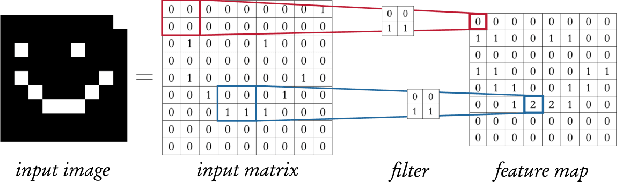
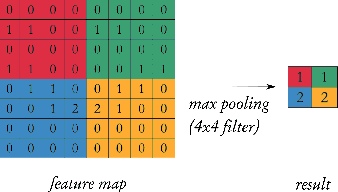
Neural networks are increasingly relied upon as components of complex safety-critical systems such as autonomous vehicles. There is high demand for tools and methods that embed neural network verification in a larger verification cycle. However, neural network verification is difficult due to a wide range of verification properties of interest, each typically only amenable to verification in specialised solvers. In this paper, we show how Imandra, a functional programming language and a theorem prover originally designed for verification, validation and simulation of financial infrastructure can offer a holistic infrastructure for neural network verification. We develop a novel library CheckINN that formalises neural networks in Imandra, and covers different important facets of neural network verification.

Proceedings of the Sixteenth International Workshop on the ACL2 Theorem Prover and its Applications

This volume contains a selection of papers presented at the 16th International Workshop on the ACL2 Theorem Prover and its Applications (ACL2-2020). The workshops are the premier technical forum for presenting research and experiences related to ACL2.