Pretrained Joint Predictions for Scalable Batch Bayesian Optimization of Molecular Designs

Batched synthesis and testing of molecular designs is the key bottleneck of drug development. There has been great interest in leveraging biomolecular foundation models as surrogates to accelerate this process. In this work, we show how to obtain scalable probabilistic surrogates of binding affinity for use in Batch Bayesian Optimization (Batch BO). This demands parallel acquisition functions that hedge between designs and the ability to rapidly sample from a joint predictive density to approximate them. Through the framework of Epistemic Neural Networks (ENNs), we obtain scalable joint predictive distributions of binding affinity on top of representations taken from large structure-informed models. Key to this work is an investigation into the importance of prior networks in ENNs and how to pretrain them on synthetic data to improve downstream performance in Batch BO. Their utility is demonstrated by rediscovering known potent EGFR inhibitors on a semi-synthetic benchmark in up to 5x fewer iterations, as well as potent inhibitors from a real-world small-molecule library in up to 10x fewer iterations, offering a promising solution for large-scale drug discovery applications.

Generalizability of density functionals learned from differentiable programming on weakly correlated spin-polarized systems

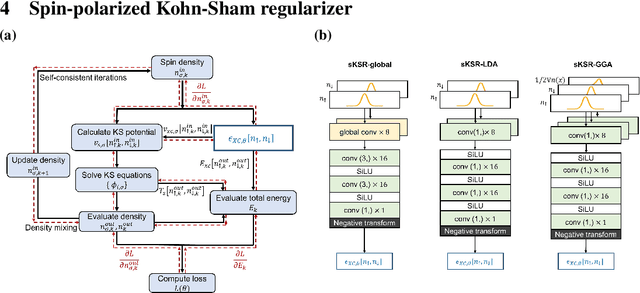
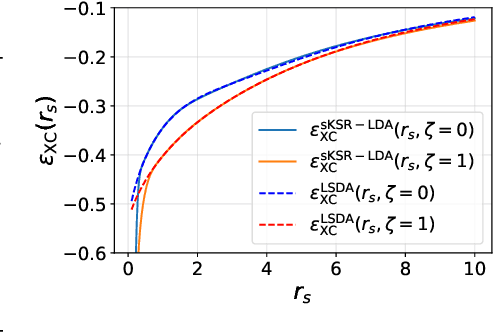
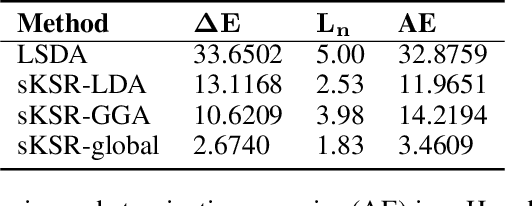
Kohn-Sham regularizer (KSR) is a machine learning approach that optimizes a physics-informed exchange-correlation functional within a differentiable Kohn-Sham density functional theory framework. We evaluate the generalizability of KSR by training on atomic systems and testing on molecules at equilibrium. We propose a spin-polarized version of KSR with local, semilocal, and nonlocal approximations for the exchange-correlation functional. The generalization error from our semilocal approximation is comparable to other differentiable approaches. Our nonlocal functional outperforms any existing machine learning functionals by predicting the ground-state energies of the test systems with a mean absolute error of 2.7 milli-Hartrees.

Kohn-Sham equations as regularizer: building prior knowledge into machine-learned physics

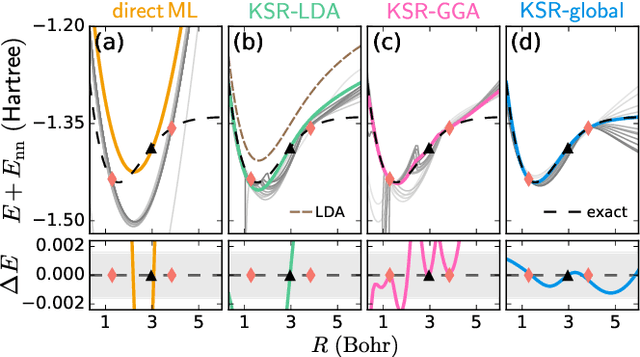
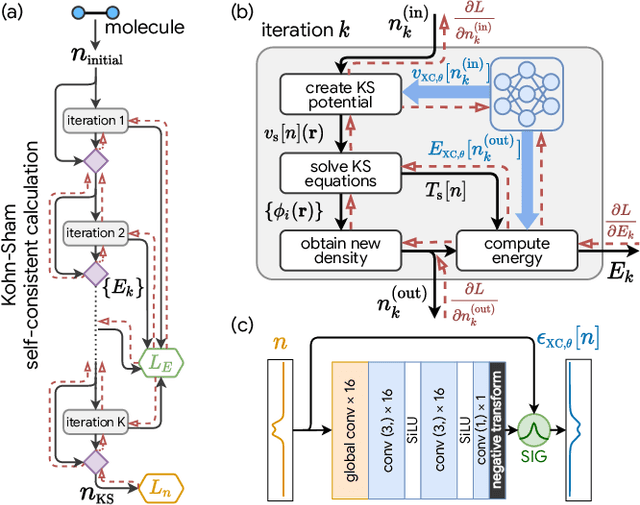
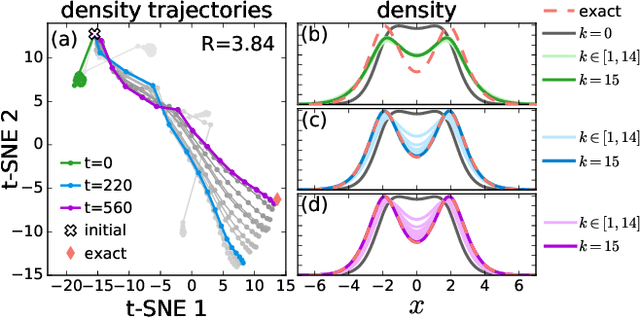
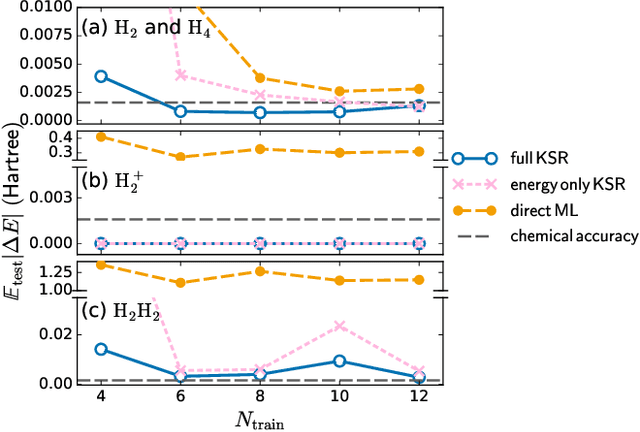
Including prior knowledge is important for effective machine learning models in physics, and is usually achieved by explicitly adding loss terms or constraints on model architectures. Prior knowledge embedded in the physics computation itself rarely draws attention. We show that solving the Kohn-Sham equations when training neural networks for the exchange-correlation functional provides an implicit regularization that greatly improves generalization. Two separations suffice for learning the entire one-dimensional H$_2$ dissociation curve within chemical accuracy, including the strongly correlated region. Our models also generalize to unseen types of molecules and overcome self-interaction error.