Using Machine Learning to Find New Density Functionals

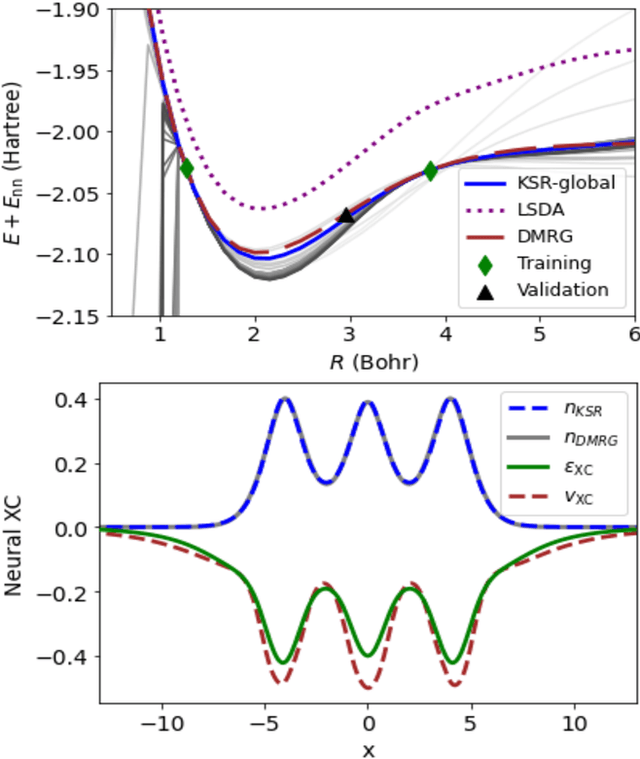
Machine learning has now become an integral part of research and innovation. The field of machine learning density functional theory has continuously expanded over the years while making several noticeable advances. We briefly discuss the status of this field and point out some current and future challenges. We also talk about how state-of-the-art science and technology tools can help overcome these challenges. This draft is a part of the "Roadmap on Machine Learning in Electronic Structure" to be published in Electronic Structure (EST).

Generalizability of density functionals learned from differentiable programming on weakly correlated spin-polarized systems

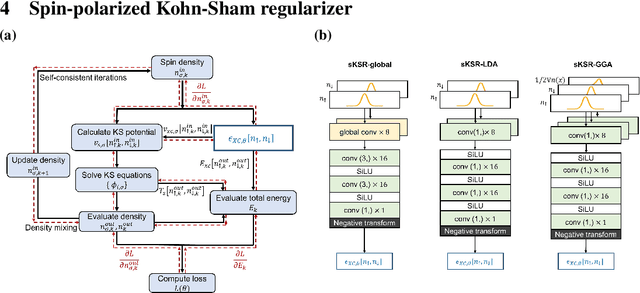
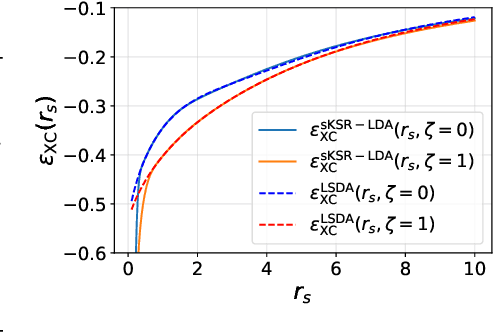
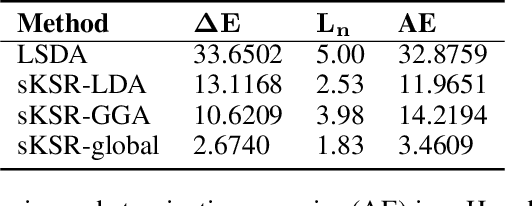
Kohn-Sham regularizer (KSR) is a machine learning approach that optimizes a physics-informed exchange-correlation functional within a differentiable Kohn-Sham density functional theory framework. We evaluate the generalizability of KSR by training on atomic systems and testing on molecules at equilibrium. We propose a spin-polarized version of KSR with local, semilocal, and nonlocal approximations for the exchange-correlation functional. The generalization error from our semilocal approximation is comparable to other differentiable approaches. Our nonlocal functional outperforms any existing machine learning functionals by predicting the ground-state energies of the test systems with a mean absolute error of 2.7 milli-Hartrees.

Kohn-Sham equations as regularizer: building prior knowledge into machine-learned physics

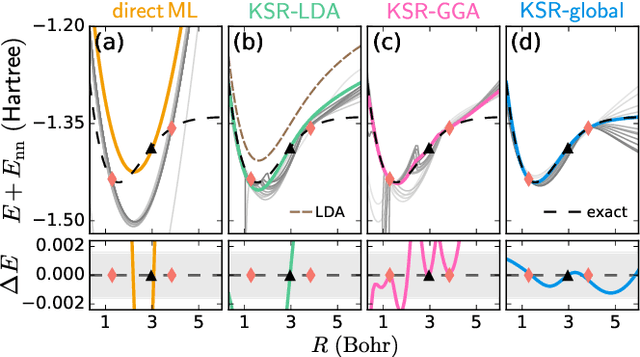
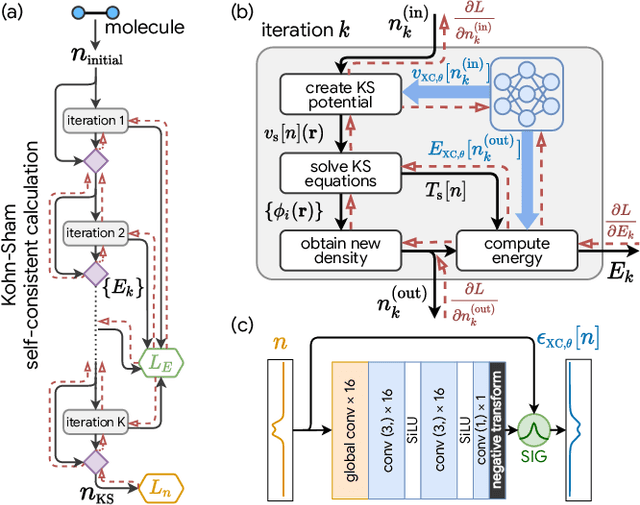
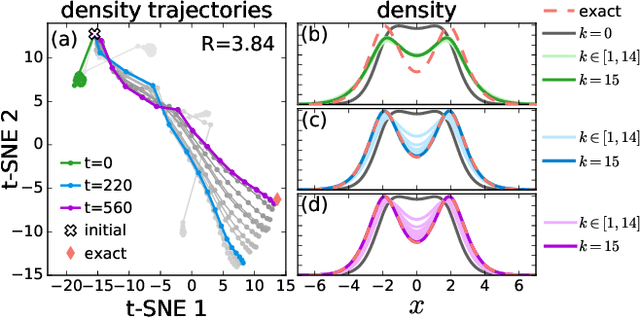
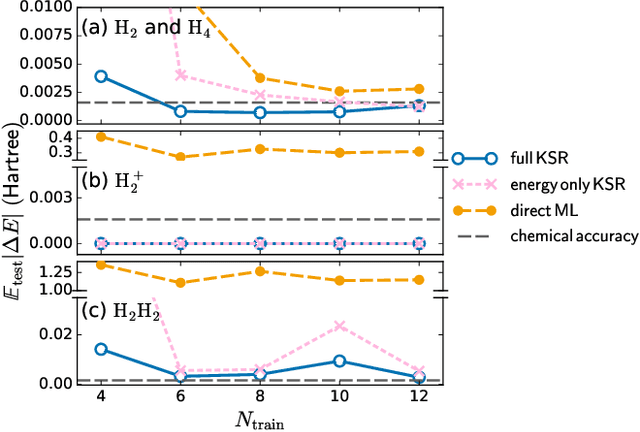
Including prior knowledge is important for effective machine learning models in physics, and is usually achieved by explicitly adding loss terms or constraints on model architectures. Prior knowledge embedded in the physics computation itself rarely draws attention. We show that solving the Kohn-Sham equations when training neural networks for the exchange-correlation functional provides an implicit regularization that greatly improves generalization. Two separations suffice for learning the entire one-dimensional H$_2$ dissociation curve within chemical accuracy, including the strongly correlated region. Our models also generalize to unseen types of molecules and overcome self-interaction error.

By-passing the Kohn-Sham equations with machine learning

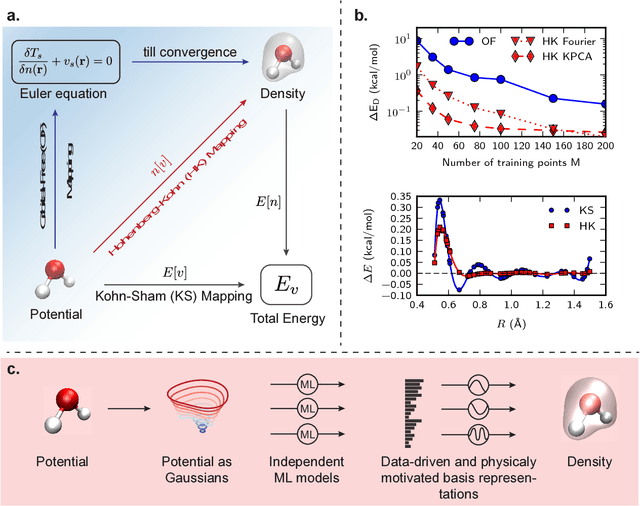
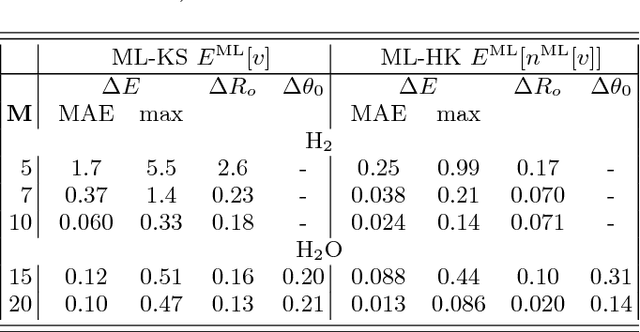
Last year, at least 30,000 scientific papers used the Kohn-Sham scheme of density functional theory to solve electronic structure problems in a wide variety of scientific fields, ranging from materials science to biochemistry to astrophysics. Machine learning holds the promise of learning the kinetic energy functional via examples, by-passing the need to solve the Kohn-Sham equations. This should yield substantial savings in computer time, allowing either larger systems or longer time-scales to be tackled, but attempts to machine-learn this functional have been limited by the need to find its derivative. The present work overcomes this difficulty by directly learning the density-potential and energy-density maps for test systems and various molecules. Both improved accuracy and lower computational cost with this method are demonstrated by reproducing DFT energies for a range of molecular geometries generated during molecular dynamics simulations. Moreover, the methodology could be applied directly to quantum chemical calculations, allowing construction of density functionals of quantum-chemical accuracy.

Understanding Kernel Ridge Regression: Common behaviors from simple functions to density functionals

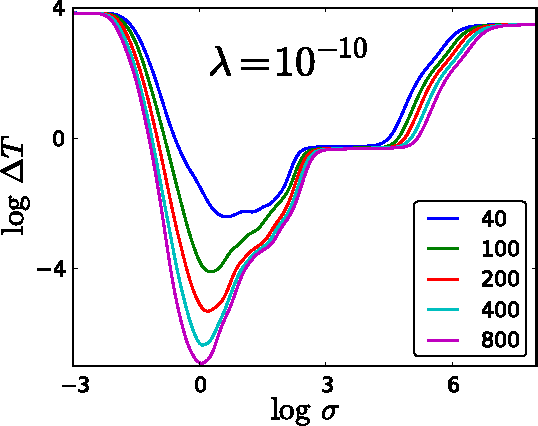
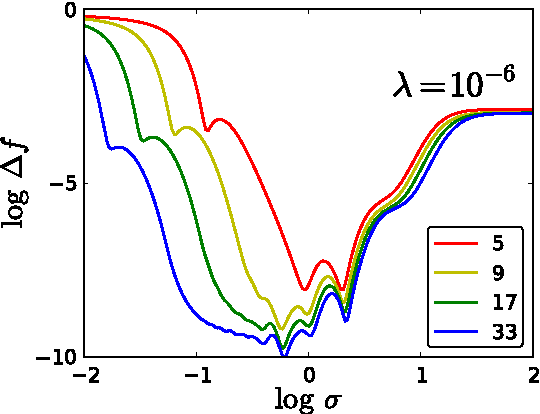
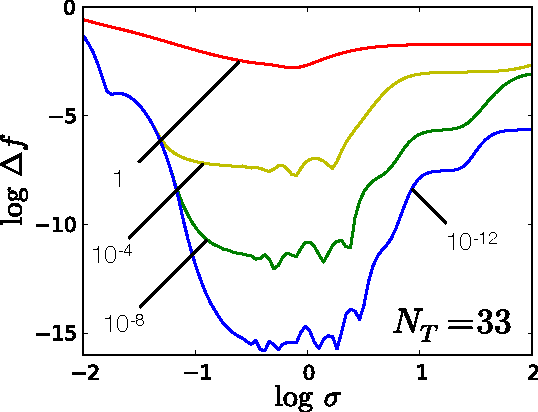
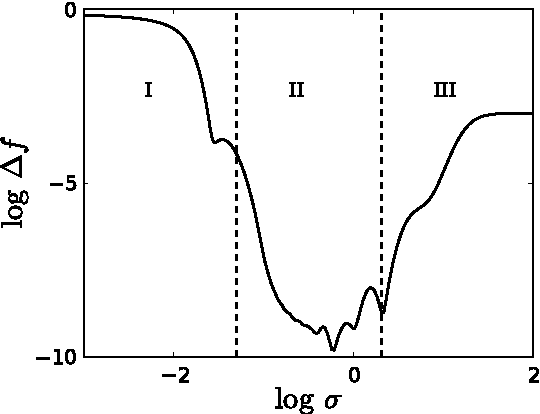
Accurate approximations to density functionals have recently been obtained via machine learning (ML). By applying ML to a simple function of one variable without any random sampling, we extract the qualitative dependence of errors on hyperparameters. We find universal features of the behavior in extreme limits, including both very small and very large length scales, and the noise-free limit. We show how such features arise in ML models of density functionals.

Understanding Machine-learned Density Functionals

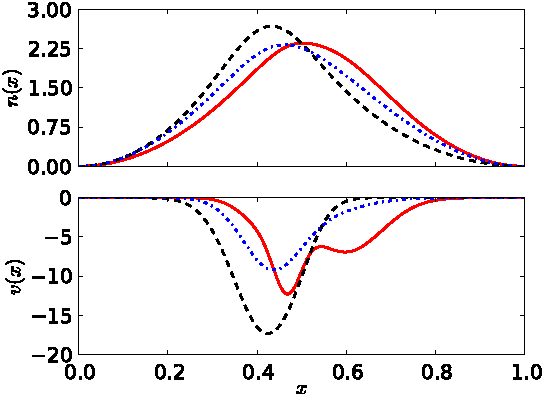
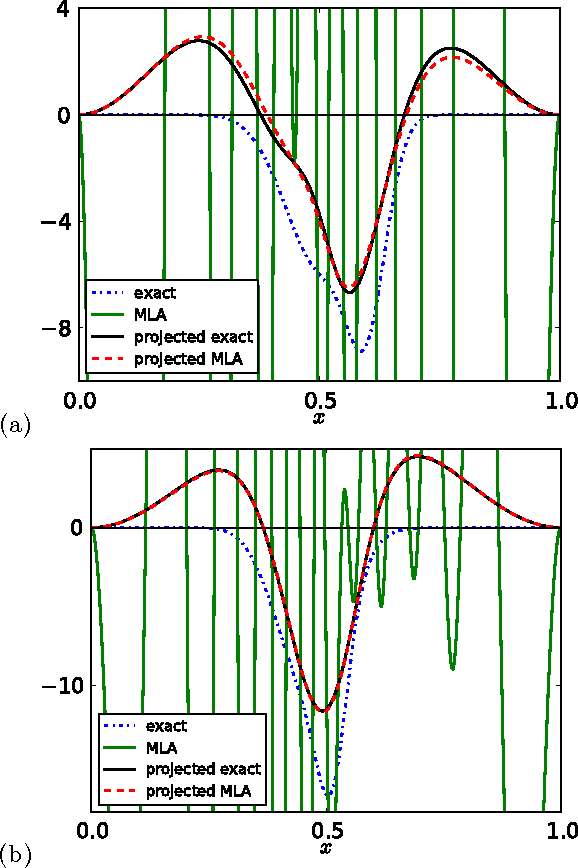
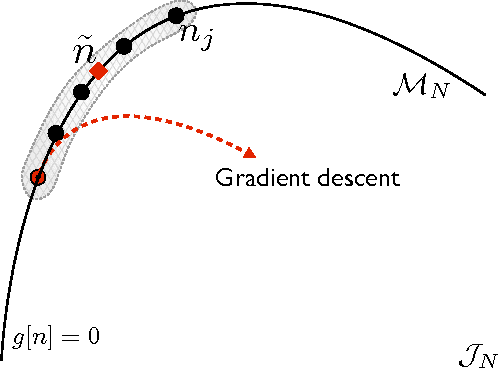
Kernel ridge regression is used to approximate the kinetic energy of non-interacting fermions in a one-dimensional box as a functional of their density. The properties of different kernels and methods of cross-validation are explored, and highly accurate energies are achieved. Accurate {\em constrained optimal densities} are found via a modified Euler-Lagrange constrained minimization of the total energy. A projected gradient descent algorithm is derived using local principal component analysis. Additionally, a sparse grid representation of the density can be used without degrading the performance of the methods. The implications for machine-learned density functional approximations are discussed.

Orbital-free Bond Breaking via Machine Learning

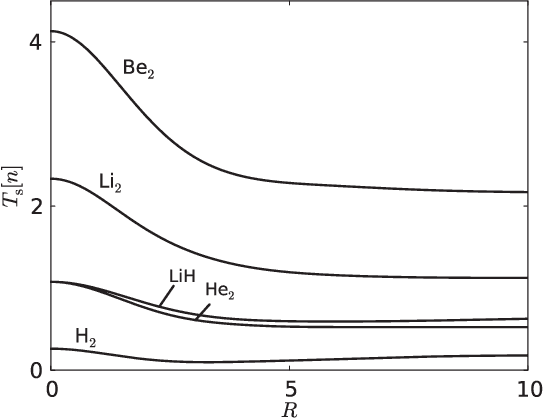
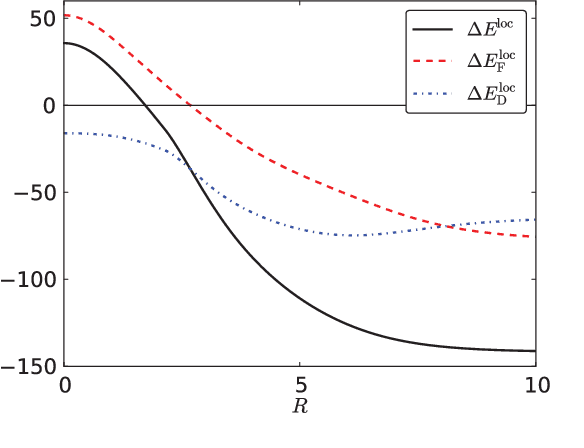
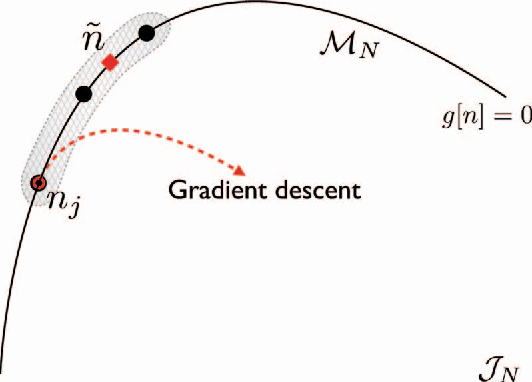
Machine learning is used to approximate the kinetic energy of one dimensional diatomics as a functional of the electron density. The functional can accurately dissociate a diatomic, and can be systematically improved with training. Highly accurate self-consistent densities and molecular forces are found, indicating the possibility for ab-initio molecular dynamics simulations.

Finding Density Functionals with Machine Learning

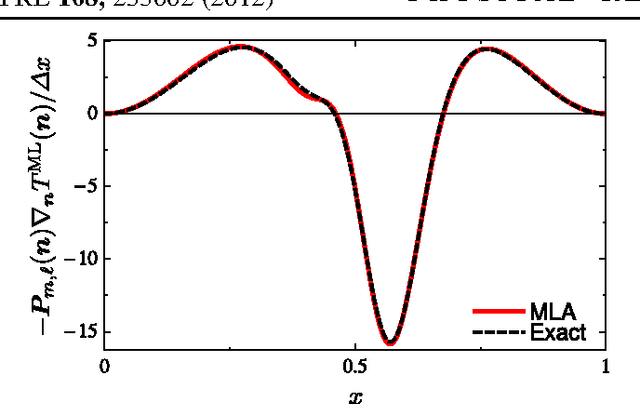
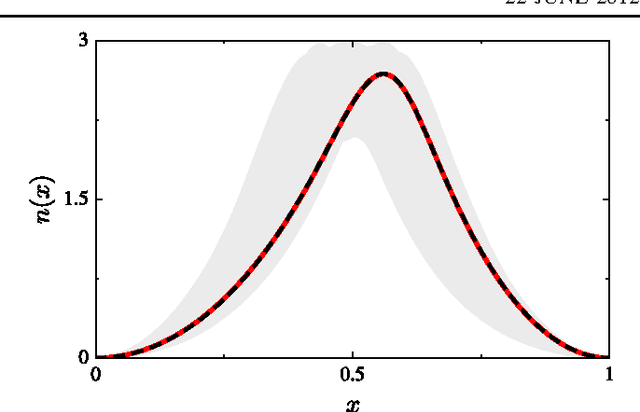
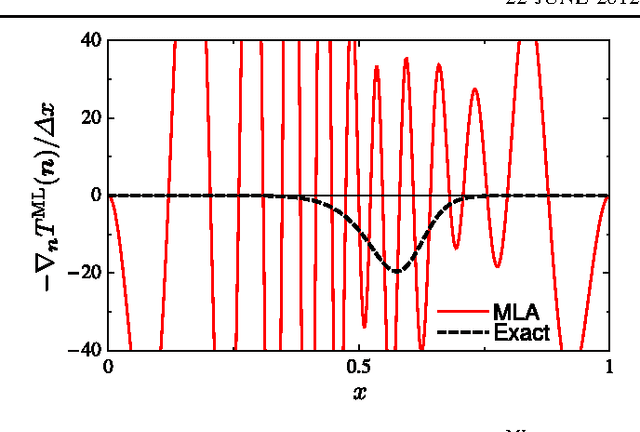
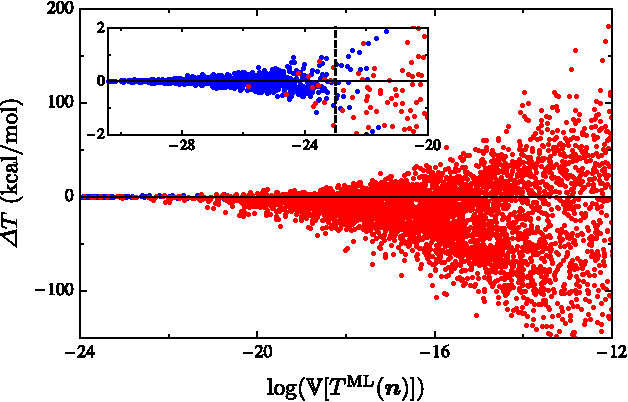
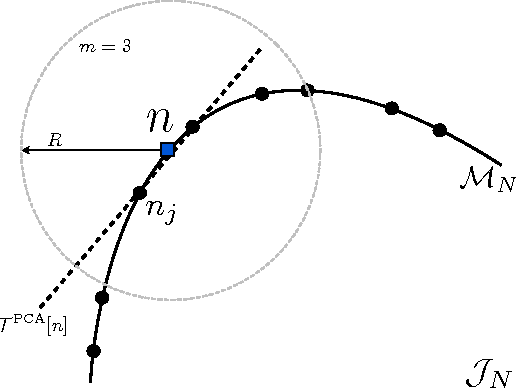
Machine learning is used to approximate density functionals. For the model problem of the kinetic energy of non-interacting fermions in 1d, mean absolute errors below 1 kcal/mol on test densities similar to the training set are reached with fewer than 100 training densities. A predictor identifies if a test density is within the interpolation region. Via principal component analysis, a projected functional derivative finds highly accurate self-consistent densities. Challenges for application of our method to real electronic structure problems are discussed.