Propagation Kernels

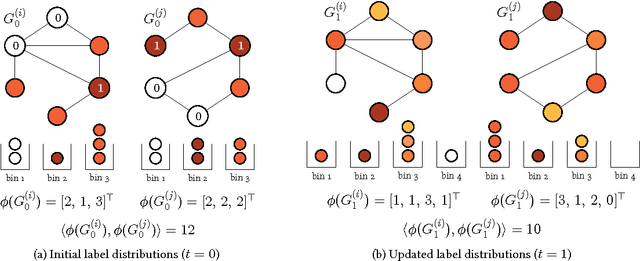
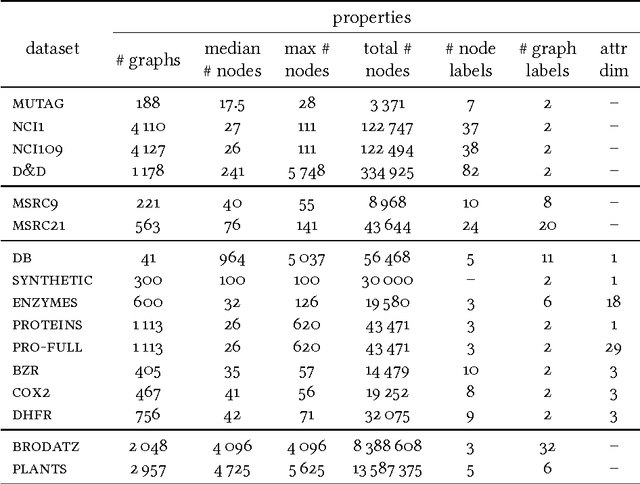
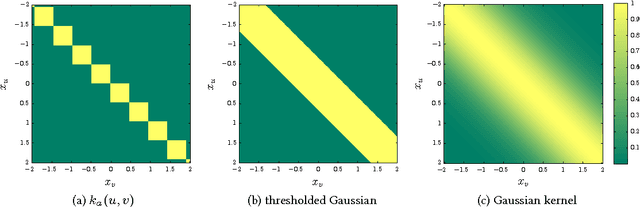
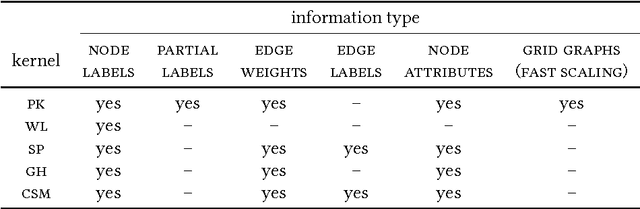
We introduce propagation kernels, a general graph-kernel framework for efficiently measuring the similarity of structured data. Propagation kernels are based on monitoring how information spreads through a set of given graphs. They leverage early-stage distributions from propagation schemes such as random walks to capture structural information encoded in node labels, attributes, and edge information. This has two benefits. First, off-the-shelf propagation schemes can be used to naturally construct kernels for many graph types, including labeled, partially labeled, unlabeled, directed, and attributed graphs. Second, by leveraging existing efficient and informative propagation schemes, propagation kernels can be considerably faster than state-of-the-art approaches without sacrificing predictive performance. We will also show that if the graphs at hand have a regular structure, for instance when modeling image or video data, one can exploit this regularity to scale the kernel computation to large databases of graphs with thousands of nodes. We support our contributions by exhaustive experiments on a number of real-world graphs from a variety of application domains.

Active Learning of Linear Embeddings for Gaussian Processes

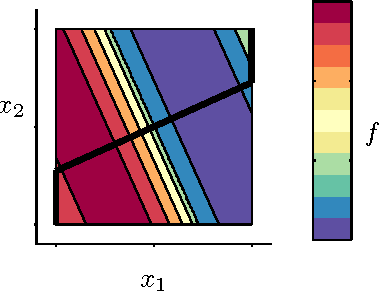
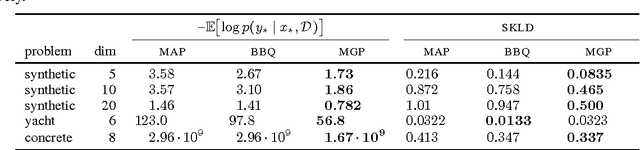
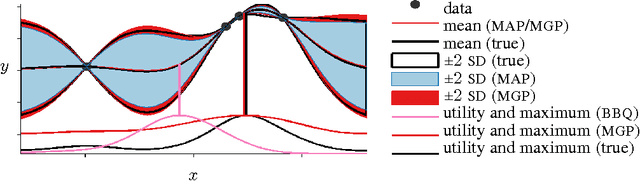
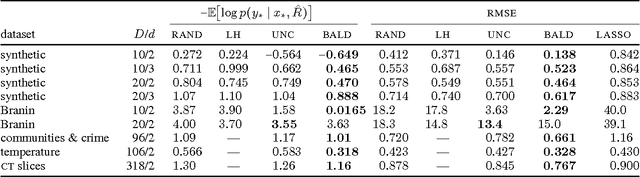
We propose an active learning method for discovering low-dimensional structure in high-dimensional Gaussian process (GP) tasks. Such problems are increasingly frequent and important, but have hitherto presented severe practical difficulties. We further introduce a novel technique for approximately marginalizing GP hyperparameters, yielding marginal predictions robust to hyperparameter mis-specification. Our method offers an efficient means of performing GP regression, quadrature, or Bayesian optimization in high-dimensional spaces.

Submodularity in Batch Active Learning and Survey Problems on Gaussian Random Fields

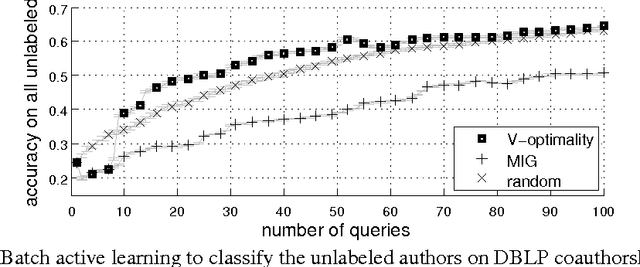
Many real-world datasets can be represented in the form of a graph whose edge weights designate similarities between instances. A discrete Gaussian random field (GRF) model is a finite-dimensional Gaussian process (GP) whose prior covariance is the inverse of a graph Laplacian. Minimizing the trace of the predictive covariance Sigma (V-optimality) on GRFs has proven successful in batch active learning classification problems with budget constraints. However, its worst-case bound has been missing. We show that the V-optimality on GRFs as a function of the batch query set is submodular and hence its greedy selection algorithm guarantees an (1-1/e) approximation ratio. Moreover, GRF models have the absence-of-suppressor (AofS) condition. For active survey problems, we propose a similar survey criterion which minimizes 1'(Sigma)1. In practice, V-optimality criterion performs better than GPs with mutual information gain criteria and allows nonuniform costs for different nodes.

Bayesian Optimal Active Search and Surveying

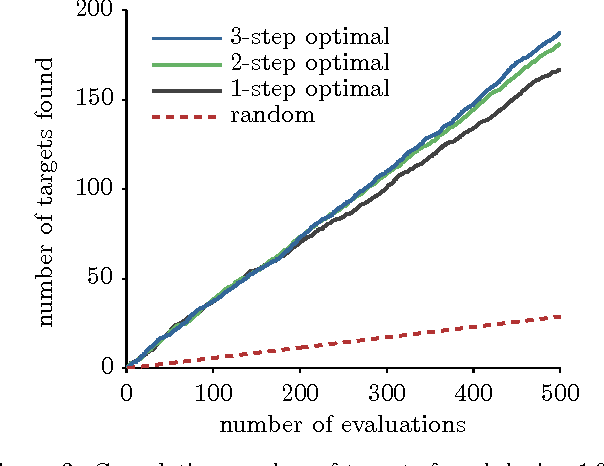
We consider two active binary-classification problems with atypical objectives. In the first, active search, our goal is to actively uncover as many members of a given class as possible. In the second, active surveying, our goal is to actively query points to ultimately predict the proportion of a given class. Numerous real-world problems can be framed in these terms, and in either case typical model-based concerns such as generalization error are only of secondary importance. We approach these problems via Bayesian decision theory; after choosing natural utility functions, we derive the optimal policies. We provide three contributions. In addition to introducing the active surveying problem, we extend previous work on active search in two ways. First, we prove a novel theoretical result, that less-myopic approximations to the optimal policy can outperform more-myopic approximations by any arbitrary degree. We then derive bounds that for certain models allow us to reduce (in practice dramatically) the exponential search space required by a naive implementation of the optimal policy, enabling further lookahead while still ensuring that optimal decisions are always made.