Learning in Budgeted Auctions with Spacing Objectives

In many repeated auction settings, participants care not only about how frequently they win but also how their winnings are distributed over time. This problem arises in various practical domains where avoiding congested demand is crucial, such as online retail sales and compute services, as well as in advertising campaigns that require sustained visibility over time. We introduce a simple model of this phenomenon, modeling it as a budgeted auction where the value of a win is a concave function of the time since the last win. This implies that for a given number of wins, even spacing over time is optimal. We also extend our model and results to the case when not all wins result in "conversions" (realization of actual gains), and the probability of conversion depends on a context. The goal is to maximize and evenly space conversions rather than just wins. We study the optimal policies for this setting in second-price auctions and offer learning algorithms for the bidders that achieve low regret against the optimal bidding policy in a Bayesian online setting. Our main result is a computationally efficient online learning algorithm that achieves $\tilde O(\sqrt T)$ regret. We achieve this by showing that an infinite-horizon Markov decision process (MDP) with the budget constraint in expectation is essentially equivalent to our problem, even when limiting that MDP to a very small number of states. The algorithm achieves low regret by learning a bidding policy that chooses bids as a function of the context and the system's state, which will be the time elapsed since the last win (or conversion). We show that state-independent strategies incur linear regret even without uncertainty of conversions. We complement this by showing that there are state-independent strategies that, while still having linear regret, achieve a $(1-\frac 1 e)$ approximation to the optimal reward.

Online Convex Optimization with Unbounded Memory

Online convex optimization (OCO) is a widely used framework in online learning. In each round, the learner chooses a decision in some convex set and an adversary chooses a convex loss function, and then the learner suffers the loss associated with their chosen decision. However, in many of the motivating applications the loss of the learner depends not only on the current decision but on the entire history of decisions until that point. The OCO framework and existing generalizations thereof fail to capture this. In this work we introduce a generalization of the OCO framework, ``Online Convex Optimization with Unbounded Memory'', that captures long-term dependence on past decisions. We introduce the notion of $p$-effective memory capacity, $H_p$, that quantifies the maximum influence of past decisions on current losses. We prove a $O(\sqrt{H_1 T})$ policy regret bound and a stronger $O(\sqrt{H_p T})$ policy regret bound under mild additional assumptions. These bounds are optimal in terms of their dependence on the time horizon $T$. We show the broad applicability of our framework by using it to derive regret bounds, and to simplify existing regret bound derivations, for a variety of online learning problems including an online variant of performative prediction and online linear control.

Non-monotonic Resource Utilization in the Bandits with Knapsacks Problem

Bandits with knapsacks (BwK) is an influential model of sequential decision-making under uncertainty that incorporates resource consumption constraints. In each round, the decision-maker observes an outcome consisting of a reward and a vector of nonnegative resource consumptions, and the budget of each resource is decremented by its consumption. In this paper we introduce a natural generalization of the stochastic BwK problem that allows non-monotonic resource utilization. In each round, the decision-maker observes an outcome consisting of a reward and a vector of resource drifts that can be positive, negative or zero, and the budget of each resource is incremented by its drift. Our main result is a Markov decision process (MDP) policy that has constant regret against a linear programming (LP) relaxation when the decision-maker knows the true outcome distributions. We build upon this to develop a learning algorithm that has logarithmic regret against the same LP relaxation when the decision-maker does not know the true outcome distributions. We also present a reduction from BwK to our model that shows our regret bound matches existing results.

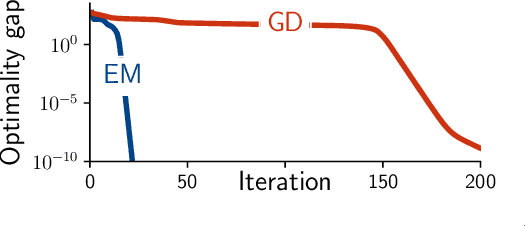
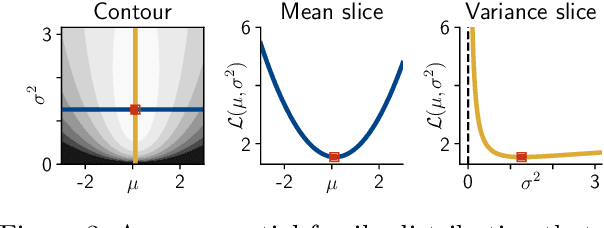
Homeomorphic-Invariance of EM: Non-Asymptotic Convergence in KL Divergence for Exponential Families via Mirror Descent

Expectation maximization (EM) is the default algorithm for fitting probabilistic models with missing or latent variables, yet we lack a full understanding of its non-asymptotic convergence properties. Previous works show results along the lines of "EM converges at least as fast as gradient descent" by assuming the conditions for the convergence of gradient descent apply to EM. This approach is not only loose, in that it does not capture that EM can make more progress than a gradient step, but the assumptions fail to hold for textbook examples of EM like Gaussian mixtures. In this work we first show that for the common setting of exponential family distributions, viewing EM as a mirror descent algorithm leads to convergence rates in Kullback-Leibler (KL) divergence. Then, we show how the KL divergence is related to first-order stationarity via Bregman divergences. In contrast to previous works, the analysis is invariant to the choice of parametrization and holds with minimal assumptions. We also show applications of these ideas to local linear (and superlinear) convergence rates, generalized EM, and non-exponential family distributions.