Is Deep Image Prior in Need of a Good Education?

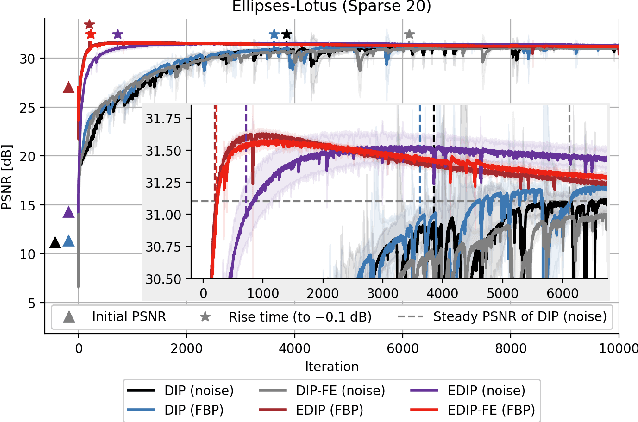
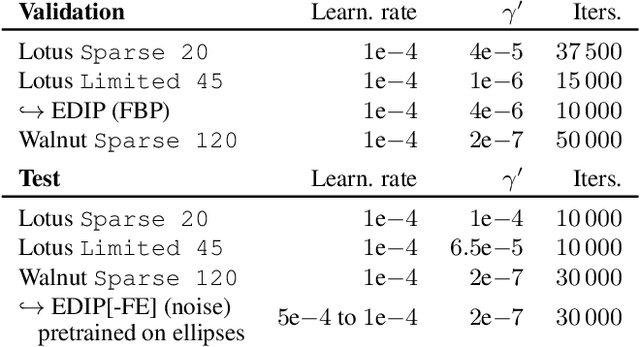
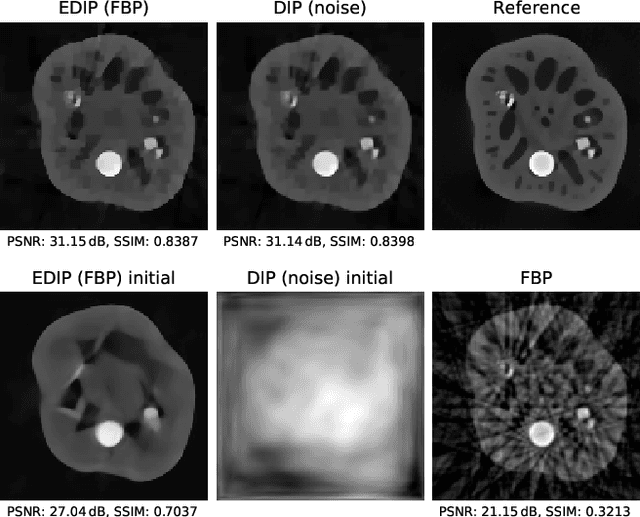
Deep image prior was recently introduced as an effective prior for image reconstruction. It represents the image to be recovered as the output of a deep convolutional neural network, and learns the network's parameters such that the output fits the corrupted observation. Despite its impressive reconstructive properties, the approach is slow when compared to learned or traditional reconstruction techniques. Our work develops a two-stage learning paradigm to address the computational challenge: (i) we perform a supervised pretraining of the network on a synthetic dataset; (ii) we fine-tune the network's parameters to adapt to the target reconstruction. We showcase that pretraining considerably speeds up the subsequent reconstruction from real-measured micro computed tomography data of biological specimens. The code and additional experimental materials are available at https://educateddip.github.io/docs.educated_deep_image_prior/.

Conditional Variational Autoencoder for Learned Image Reconstruction

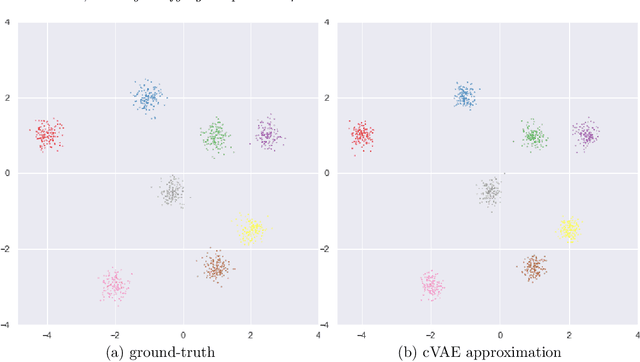
Learned image reconstruction techniques using deep neural networks have recently gained popularity, and have delivered promising empirical results. However, most approaches focus on one single recovery for each observation, and thus neglect the uncertainty information. In this work, we develop a novel computational framework that approximates the posterior distribution of the unknown image at each query observation. The proposed framework is very flexible: It handles implicit noise models and priors, it incorporates the data formation process (i.e., the forward operator), and the learned reconstructive properties are transferable between different datasets. Once the network is trained using the conditional variational autoencoder loss, it provides a computationally efficient sampler for the approximate posterior distribution via feed-forward propagation, and the summarizing statistics of the generated samples are used for both point-estimation and uncertainty quantification. We illustrate the proposed framework with extensive numerical experiments on positron emission tomography (with both moderate and low count levels) showing that the framework generates high-quality samples when compared with state-of-the-art methods.

Unsupervised Knowledge-Transfer for Learned Image Reconstruction

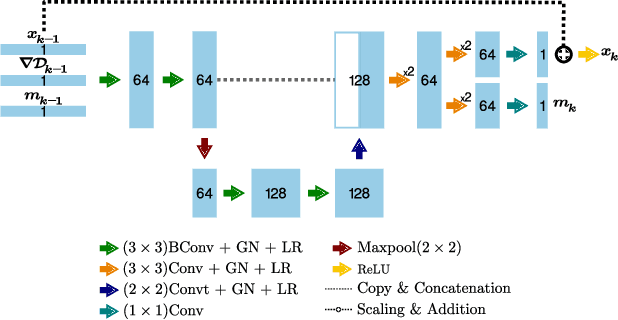
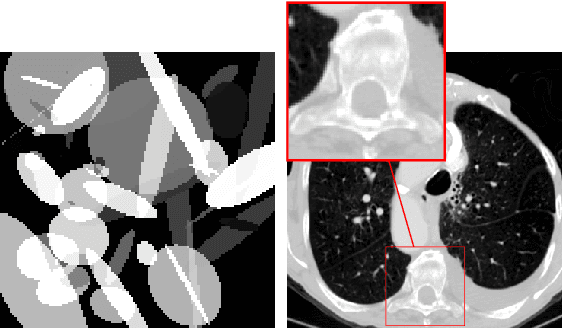
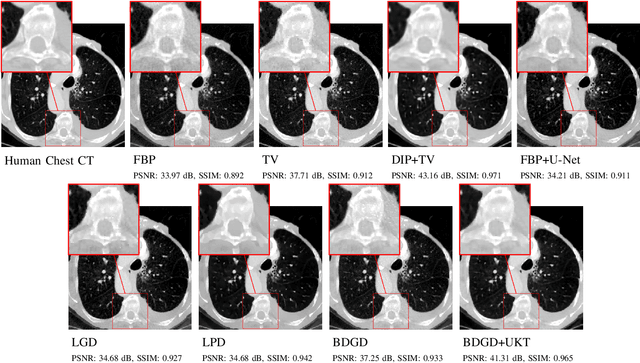
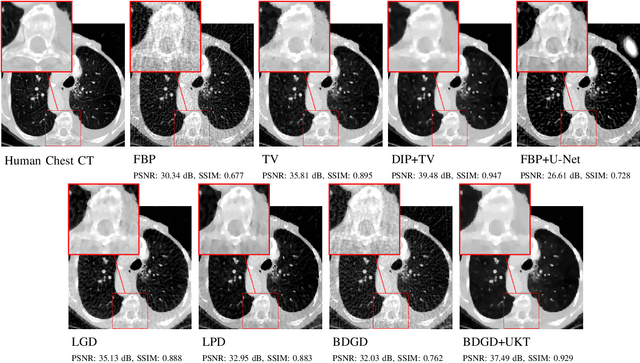
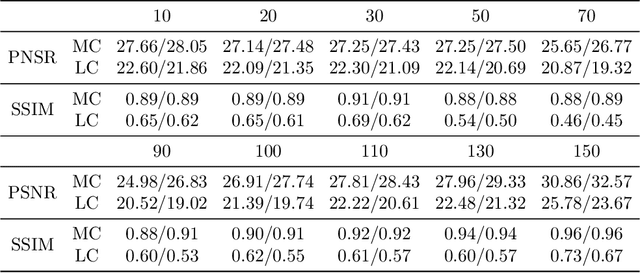
Deep learning-based image reconstruction approaches have demonstrated impressive empirical performance in many imaging modalities. These approaches generally require a large amount of high-quality training data, which is often not available. To circumvent this issue, we develop a novel unsupervised knowledge-transfer paradigm for learned iterative reconstruction within a Bayesian framework. The proposed approach learns an iterative reconstruction network in two phases. The first phase trains a reconstruction network with a set of ordered pairs comprising of ground truth images and measurement data. The second phase fine-tunes the pretrained network to the measurement data without supervision. Furthermore, the framework delivers uncertainty information over the reconstructed image. We present extensive experimental results on low-dose and sparse-view computed tomography, showing that the proposed framework significantly improves reconstruction quality not only visually, but also quantitatively in terms of PSNR and SSIM, and is competitive with several state-of-the-art supervised and unsupervised reconstruction techniques.

Quantifying Sources of Uncertainty in Deep Learning-Based Image Reconstruction

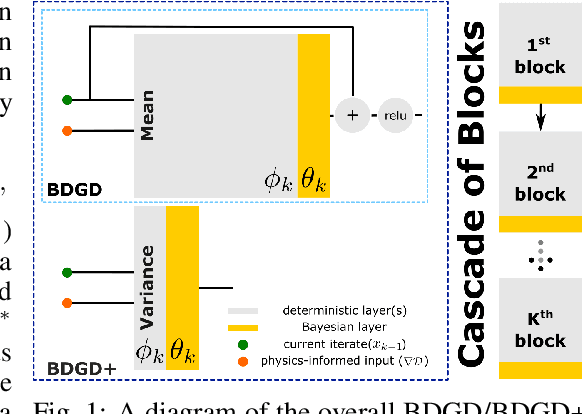
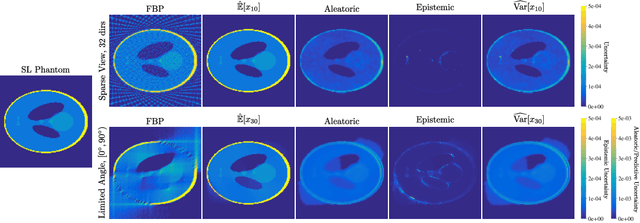
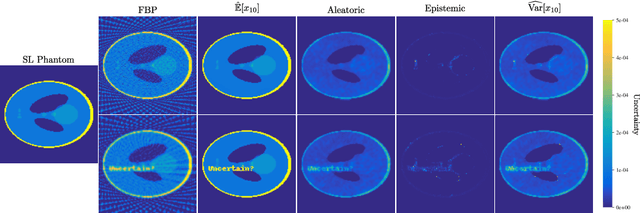
Image reconstruction methods based on deep neural networks have shown outstanding performance, equalling or exceeding the state-of-the-art results of conventional approaches, but often do not provide uncertainty information about the reconstruction. In this work we propose a scalable and efficient framework to simultaneously quantify aleatoric and epistemic uncertainties in learned iterative image reconstruction. We build on a Bayesian deep gradient descent method for quantifying epistemic uncertainty, and incorporate the heteroscedastic variance of the noise to account for the aleatoric uncertainty. We show that our method exhibits competitive performance against conventional benchmarks for computed tomography with both sparse view and limited angle data. The estimated uncertainty captures the variability in the reconstructions, caused by the restricted measurement model, and by missing information, due to the limited angle geometry.

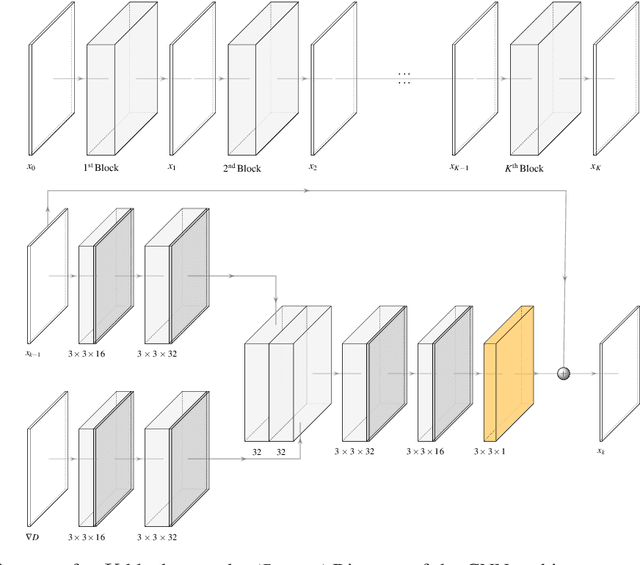
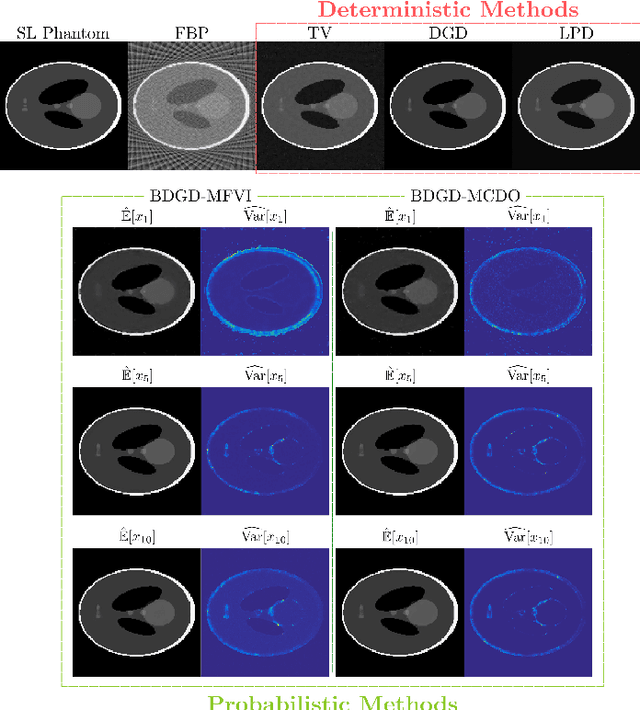
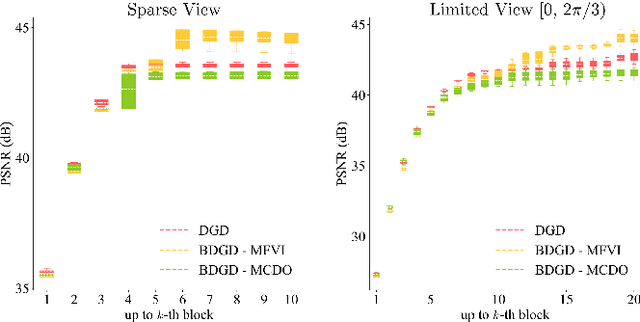
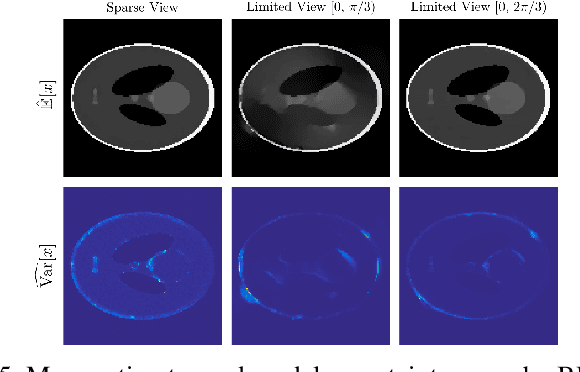
Quantifying Model Uncertainty in Inverse Problems via Bayesian Deep Gradient Descent

Recent advances in reconstruction methods for inverse problems leverage powerful data-driven models, e.g., deep neural networks. These techniques have demonstrated state-of-the-art performances for several imaging tasks, but they often do not provide uncertainty on the obtained reconstructions. In this work, we develop a novel scalable data-driven knowledge-aided computational framework to quantify the model uncertainty via Bayesian neural networks. The approach builds on and extends deep gradient descent, a recently developed greedy iterative training scheme, and recasts it within a probabilistic framework. Scalability is achieved by being hybrid in the architecture: only the last layer of each block is Bayesian, while the others remain deterministic, and by being greedy in training. The framework is showcased on one representative medical imaging modality, viz. computed tomography with either sparse view or limited view data, and exhibits competitive performance with respect to state-of-the-art benchmarks, e.g., total variation, deep gradient descent and learned primal-dual.