Neural Network Approximation of Graph Fourier Transforms for Sparse Sampling of Networked Flow Dynamics

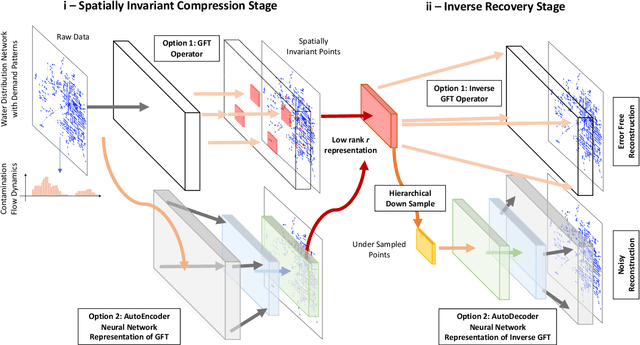
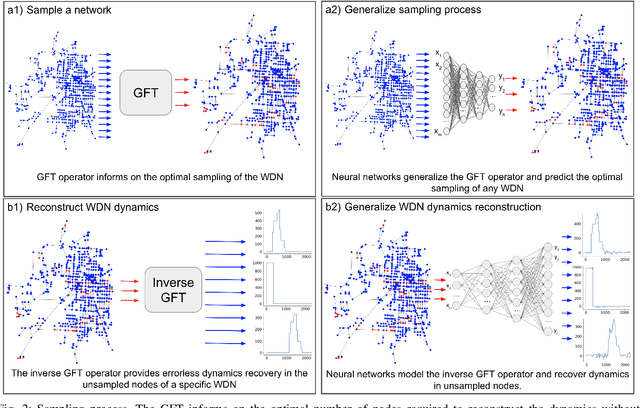
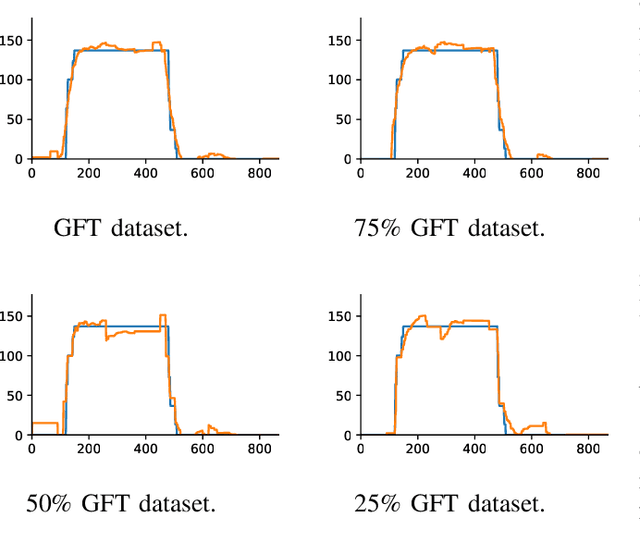
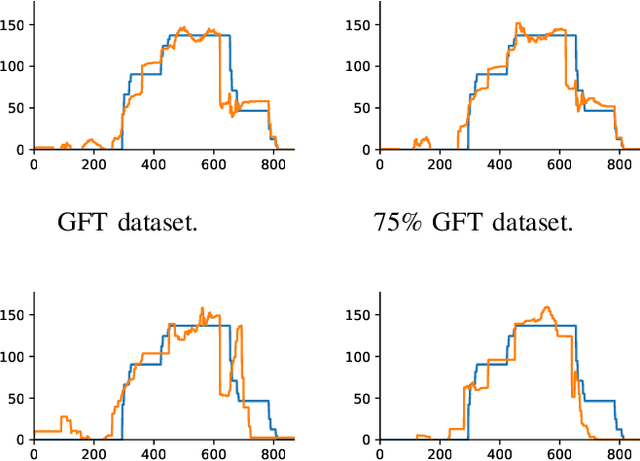
Infrastructure monitoring is critical for safe operations and sustainability. Water distribution networks (WDNs) are large-scale networked critical systems with complex cascade dynamics which are difficult to predict. Ubiquitous monitoring is expensive and a key challenge is to infer the contaminant dynamics from partial sparse monitoring data. Existing approaches use multi-objective optimisation to find the minimum set of essential monitoring points, but lack performance guarantees and a theoretical framework. Here, we first develop Graph Fourier Transform (GFT) operators to compress networked contamination spreading dynamics to identify the essential principle data collection points with inference performance guarantees. We then build autoencoder (AE) inspired neural networks (NN) to generalize the GFT sampling process and under-sample further from the initial sampling set, allowing a very small set of data points to largely reconstruct the contamination dynamics over real and artificial WDNs. Various sources of the contamination are tested and we obtain high accuracy reconstruction using around 5-10% of the sample set. This general approach of compression and under-sampled recovery via neural networks can be applied to a wide range of networked infrastructures to enable digital twins.

Adversarial recovery of agent rewards from latent spaces of the limit order book

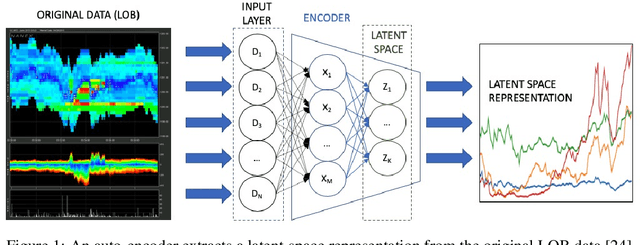
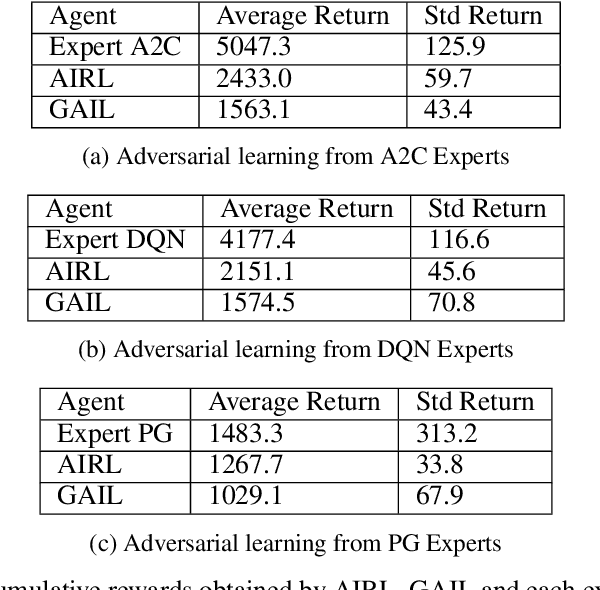
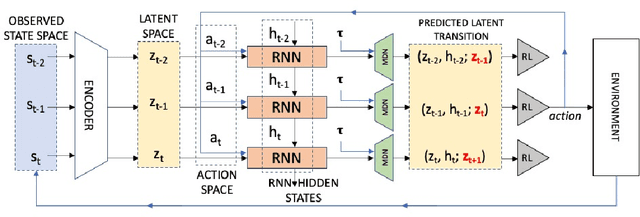
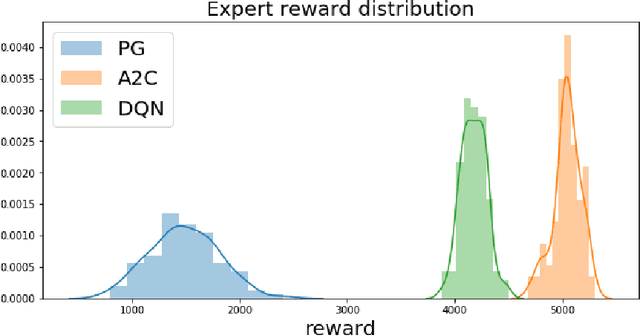
Inverse reinforcement learning has proved its ability to explain state-action trajectories of expert agents by recovering their underlying reward functions in increasingly challenging environments. Recent advances in adversarial learning have allowed extending inverse RL to applications with non-stationary environment dynamics unknown to the agents, arbitrary structures of reward functions and improved handling of the ambiguities inherent to the ill-posed nature of inverse RL. This is particularly relevant in real time applications on stochastic environments involving risk, like volatile financial markets. Moreover, recent work on simulation of complex environments enable learning algorithms to engage with real market data through simulations of its latent space representations, avoiding a costly exploration of the original environment. In this paper, we explore whether adversarial inverse RL algorithms can be adapted and trained within such latent space simulations from real market data, while maintaining their ability to recover agent rewards robust to variations in the underlying dynamics, and transfer them to new regimes of the original environment.

Counterfactual Distribution Regression for Structured Inference

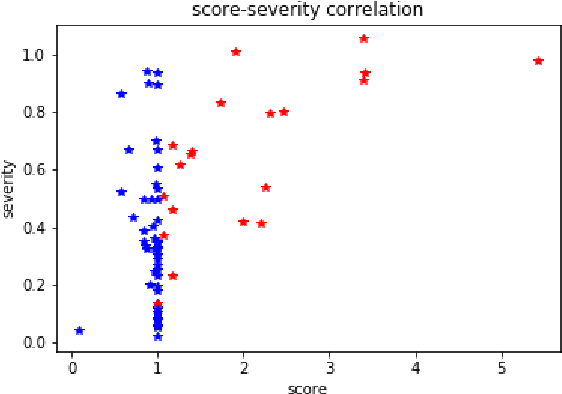
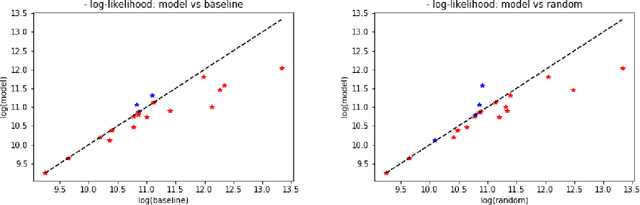
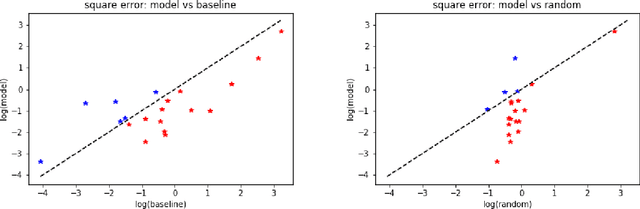
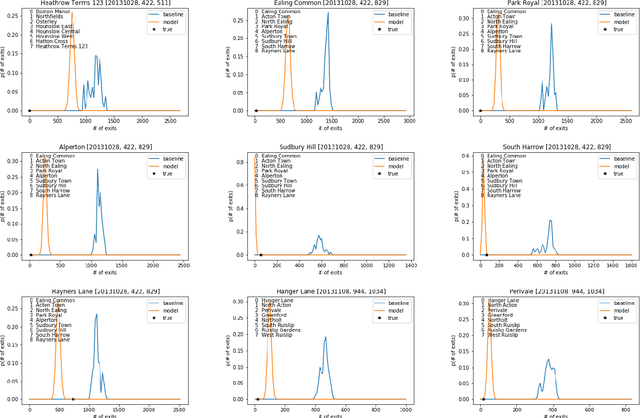
We consider problems in which a system receives external \emph{perturbations} from time to time. For instance, the system can be a train network in which particular lines are repeatedly disrupted without warning, having an effect on passenger behavior. The goal is to predict changes in the behavior of the system at particular points of interest, such as passenger traffic around stations at the affected rails. We assume that the data available provides records of the system functioning at its "natural regime" (e.g., the train network without disruptions) and data on cases where perturbations took place. The inference problem is how information concerning perturbations, with particular covariates such as location and time, can be generalized to predict the effect of novel perturbations. We approach this problem from the point of view of a mapping from the counterfactual distribution of the system behavior without disruptions to the distribution of the disrupted system. A variant on \emph{distribution regression} is developed for this setup.

The Sensitivity of Counterfactual Fairness to Unmeasured Confounding

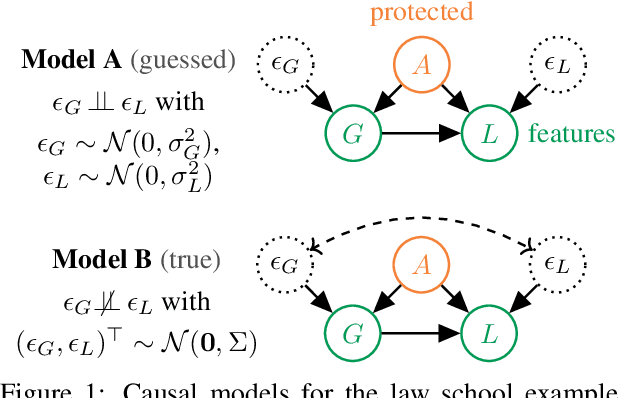
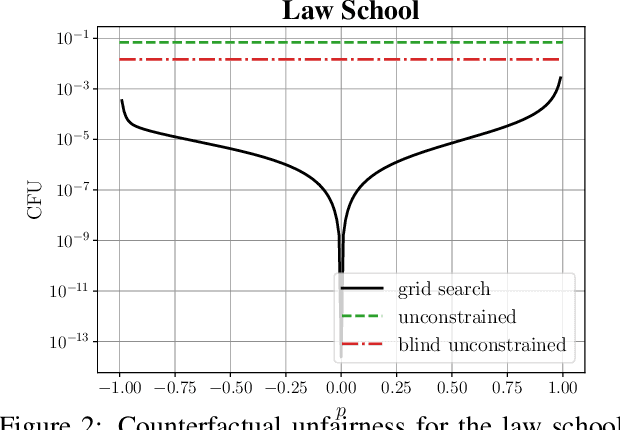
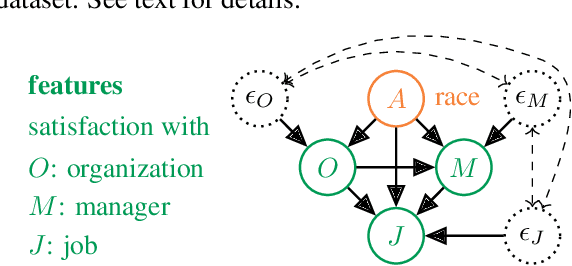
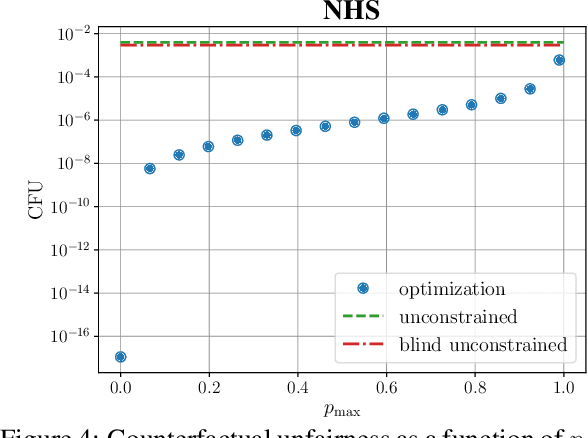
Causal approaches to fairness have seen substantial recent interest, both from the machine learning community and from wider parties interested in ethical prediction algorithms. In no small part, this has been due to the fact that causal models allow one to simultaneously leverage data and expert knowledge to remove discriminatory effects from predictions. However, one of the primary assumptions in causal modeling is that you know the causal graph. This introduces a new opportunity for bias, caused by misspecifying the causal model. One common way for misspecification to occur is via unmeasured confounding: the true causal effect between variables is partially described by unobserved quantities. In this work we design tools to assess the sensitivity of fairness measures to this confounding for the popular class of non-linear additive noise models (ANMs). Specifically, we give a procedure for computing the maximum difference between two counterfactually fair predictors, where one has become biased due to confounding. For the case of bivariate confounding our technique can be swiftly computed via a sequence of closed-form updates. For multivariate confounding we give an algorithm that can be efficiently solved via automatic differentiation. We demonstrate our new sensitivity analysis tools in real-world fairness scenarios to assess the bias arising from confounding.

Towards Inverse Reinforcement Learning for Limit Order Book Dynamics

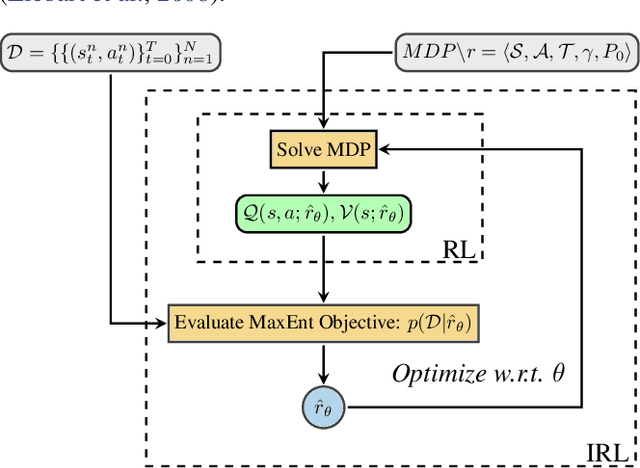
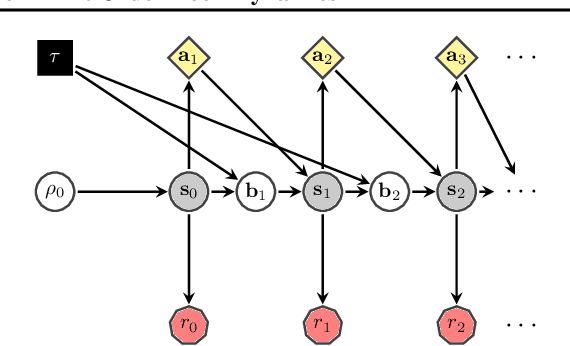
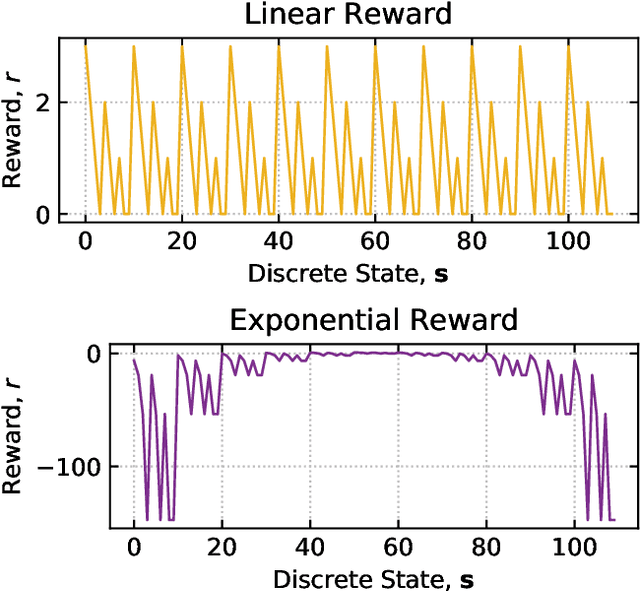
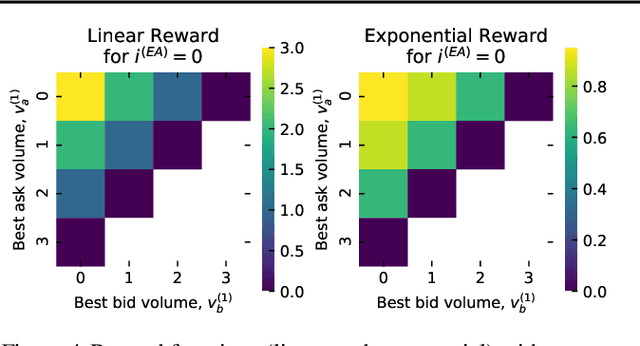
Multi-agent learning is a promising method to simulate aggregate competitive behaviour in finance. Learning expert agents' reward functions through their external demonstrations is hence particularly relevant for subsequent design of realistic agent-based simulations. Inverse Reinforcement Learning (IRL) aims at acquiring such reward functions through inference, allowing to generalize the resulting policy to states not observed in the past. This paper investigates whether IRL can infer such rewards from agents within real financial stochastic environments: limit order books (LOB). We introduce a simple one-level LOB, where the interactions of a number of stochastic agents and an expert trading agent are modelled as a Markov decision process. We consider two cases for the expert's reward: either a simple linear function of state features; or a complex, more realistic non-linear function. Given the expert agent's demonstrations, we attempt to discover their strategy by modelling their latent reward function using linear and Gaussian process (GP) regressors from previous literature, and our own approach through Bayesian neural networks (BNN). While the three methods can learn the linear case, only the GP-based and our proposed BNN methods are able to discover the non-linear reward case. Our BNN IRL algorithm outperforms the other two approaches as the number of samples increases. These results illustrate that complex behaviours, induced by non-linear reward functions amid agent-based stochastic scenarios, can be deduced through inference, encouraging the use of inverse reinforcement learning for opponent-modelling in multi-agent systems.

Neural Likelihoods via Cumulative Distribution Functions

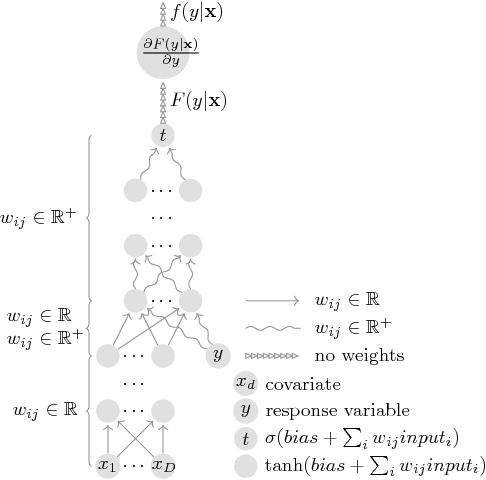
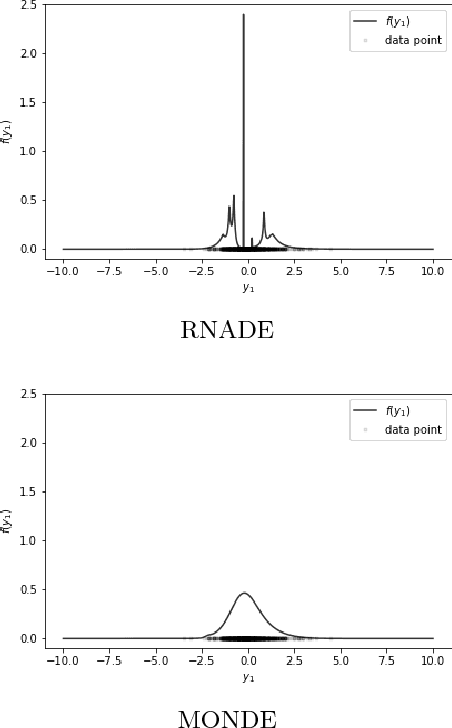
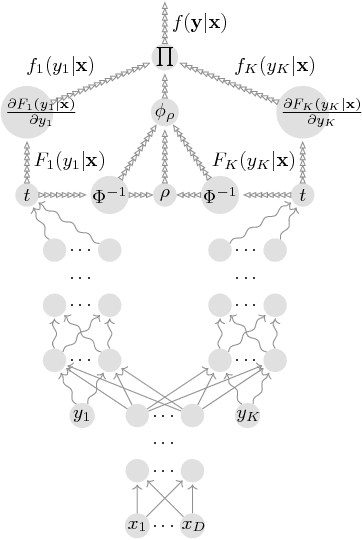
We leverage neural networks as universal approximators of monotonic functions to build a parameterization of conditional cumulative distribution functions. By a modification of backpropagation as applied both to parameters and outputs, we show that we are able to build black box density estimators which are competitive against recently proposed models, while avoiding assumptions concerning the base distribution in a mixture model. That is, it makes no use of parametric models as building blocks. This approach removes some undesirable degrees of freedom on the design on neural networks for flexible conditional density estimation, while implementation can be easily accomplished by standard algorithms readily available in popular neural network toolboxes.

Bayesian Semi-supervised Learning with Graph Gaussian Processes

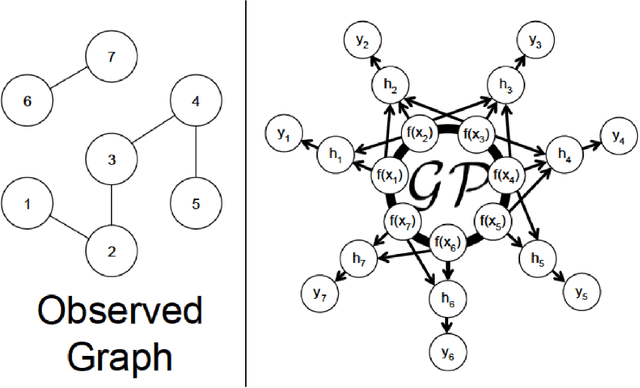
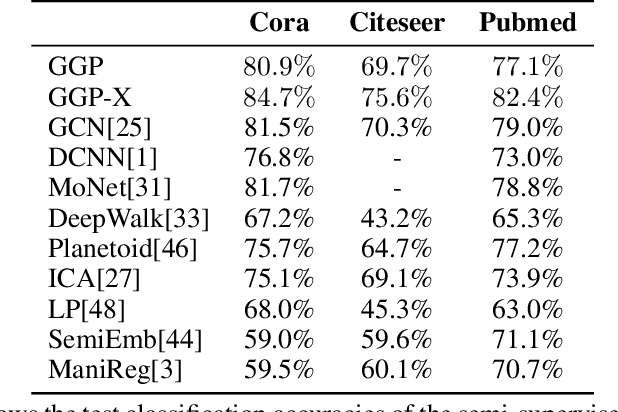
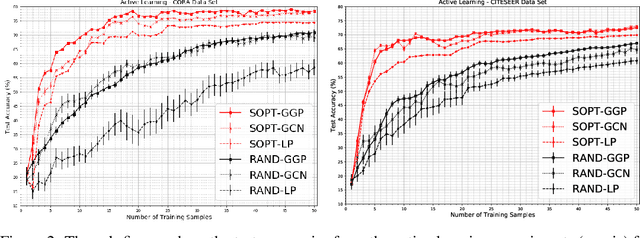
We propose a data-efficient Gaussian process-based Bayesian approach to the semi-supervised learning problem on graphs. The proposed model shows extremely competitive performance when compared to the state-of-the-art graph neural networks on semi-supervised learning benchmark experiments, and outperforms the neural networks in active learning experiments where labels are scarce. Furthermore, the model does not require a validation data set for early stopping to control over-fitting. Our model can be viewed as an instance of empirical distribution regression weighted locally by network connectivity. We further motivate the intuitive construction of the model with a Bayesian linear model interpretation where the node features are filtered by an operator related to the graph Laplacian. The method can be easily implemented by adapting off-the-shelf scalable variational inference algorithms for Gaussian processes.

Causal Interventions for Fairness

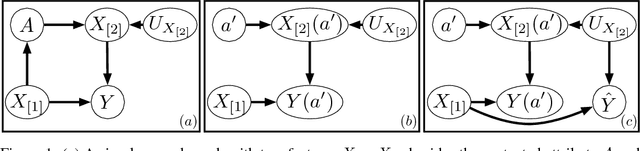
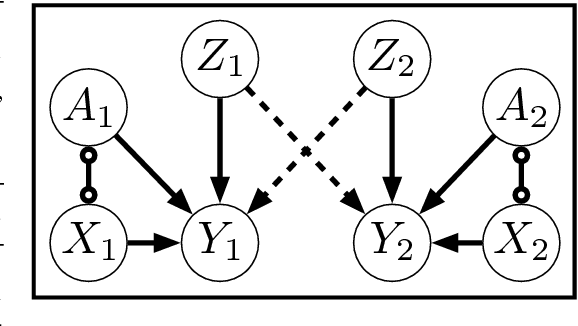
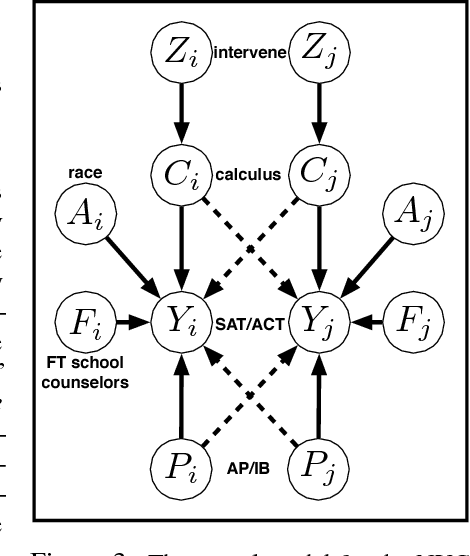
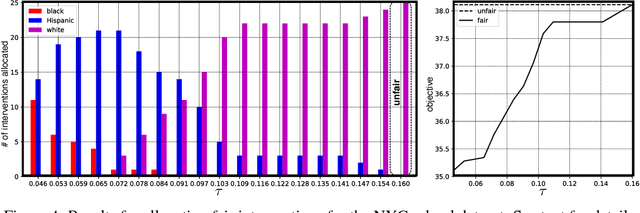
Most approaches in algorithmic fairness constrain machine learning methods so the resulting predictions satisfy one of several intuitive notions of fairness. While this may help private companies comply with non-discrimination laws or avoid negative publicity, we believe it is often too little, too late. By the time the training data is collected, individuals in disadvantaged groups have already suffered from discrimination and lost opportunities due to factors out of their control. In the present work we focus instead on interventions such as a new public policy, and in particular, how to maximize their positive effects while improving the fairness of the overall system. We use causal methods to model the effects of interventions, allowing for potential interference--each individual's outcome may depend on who else receives the intervention. We demonstrate this with an example of allocating a budget of teaching resources using a dataset of schools in New York City.

Alpha-Beta Divergence For Variational Inference

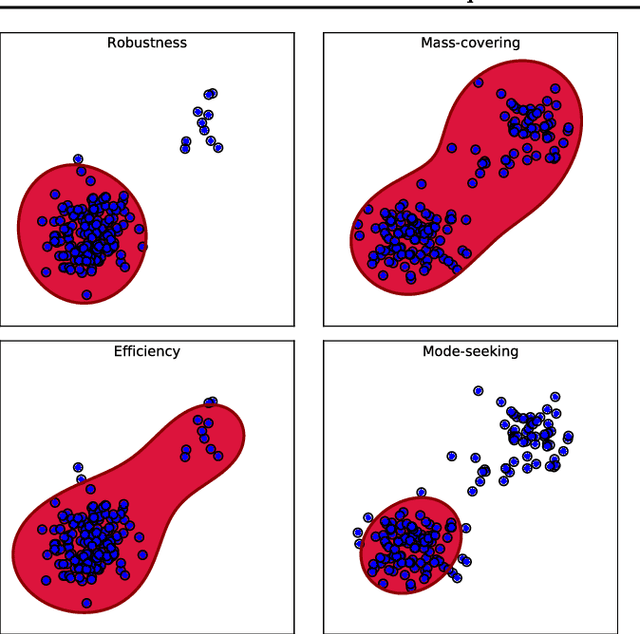
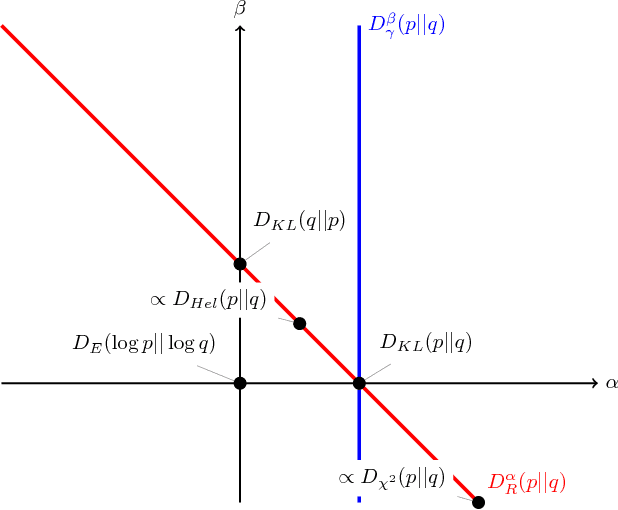
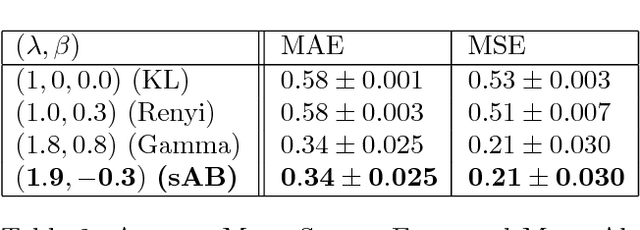
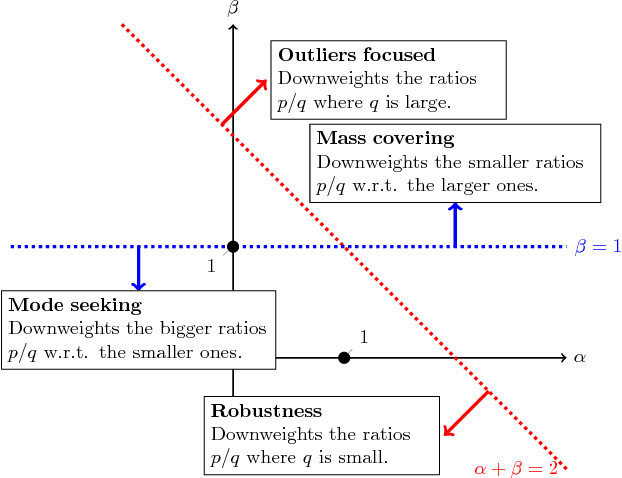
This paper introduces a variational approximation framework using direct optimization of what is known as the {\it scale invariant Alpha-Beta divergence} (sAB divergence). This new objective encompasses most variational objectives that use the Kullback-Leibler, the R{\'e}nyi or the gamma divergences. It also gives access to objective functions never exploited before in the context of variational inference. This is achieved via two easy to interpret control parameters, which allow for a smooth interpolation over the divergence space while trading-off properties such as mass-covering of a target distribution and robustness to outliers in the data. Furthermore, the sAB variational objective can be optimized directly by repurposing existing methods for Monte Carlo computation of complex variational objectives, leading to estimates of the divergence instead of variational lower bounds. We show the advantages of this objective on Bayesian models for regression problems.

Causal Reasoning for Algorithmic Fairness

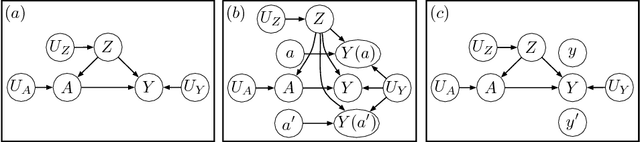
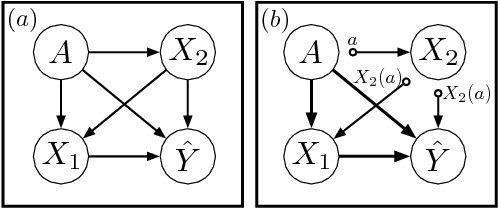
In this work, we argue for the importance of causal reasoning in creating fair algorithms for decision making. We give a review of existing approaches to fairness, describe work in causality necessary for the understanding of causal approaches, argue why causality is necessary for any approach that wishes to be fair, and give a detailed analysis of the many recent approaches to causality-based fairness.