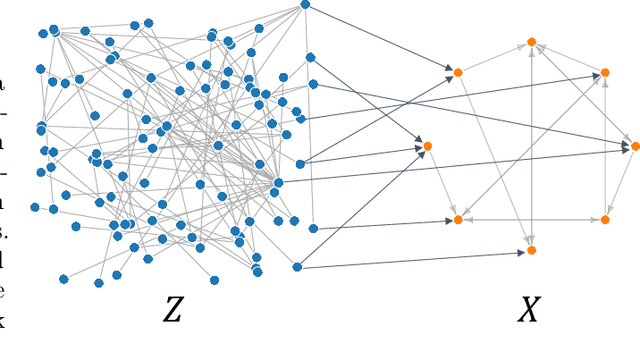
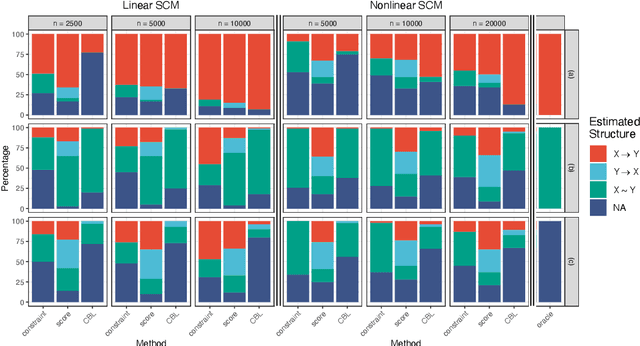
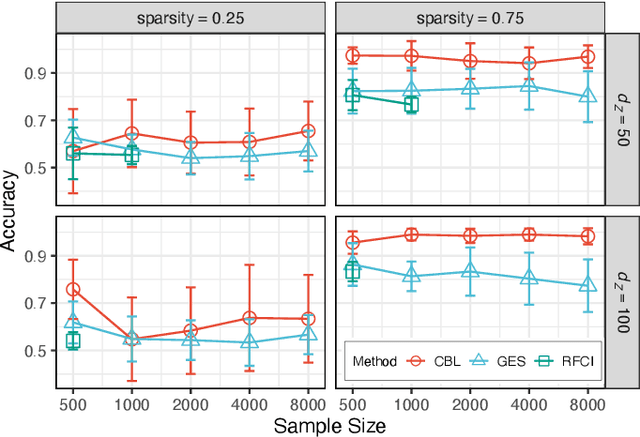
Causal discovery under a confounder blanket

Inferring causal relationships from observational data is rarely straightforward, but the problem is especially difficult in high dimensions. For these applications, causal discovery algorithms typically require parametric restrictions or extreme sparsity constraints. We relax these assumptions and focus on an important but more specialized problem, namely recovering a directed acyclic subgraph of variables known to be causally descended from some (possibly large) set of confounding covariates, i.e. a $\textit{confounder blanket}$. This is useful in many settings, for example when studying a dynamic biomolecular subsystem with genetic data providing causally relevant background information. Under a structural assumption that, we argue, must be satisfied in practice if informative answers are to be found, our method accommodates graphs of low or high sparsity while maintaining polynomial time complexity. We derive a sound and complete algorithm for identifying causal relationships under these conditions and implement testing procedures with provable error control for linear and nonlinear systems. We demonstrate our approach on a range of simulation settings.

The Causal Marginal Polytope for Bounding Treatment Effects

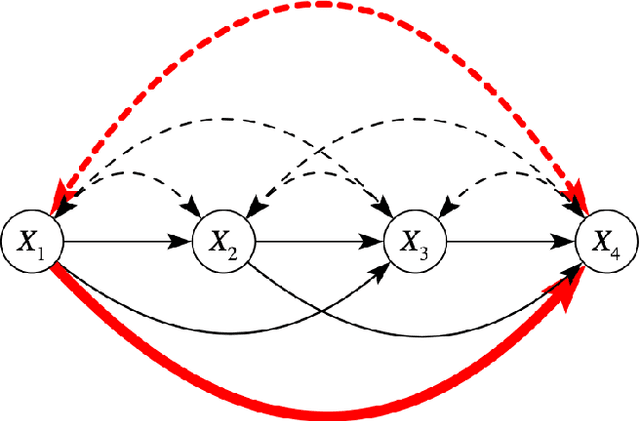
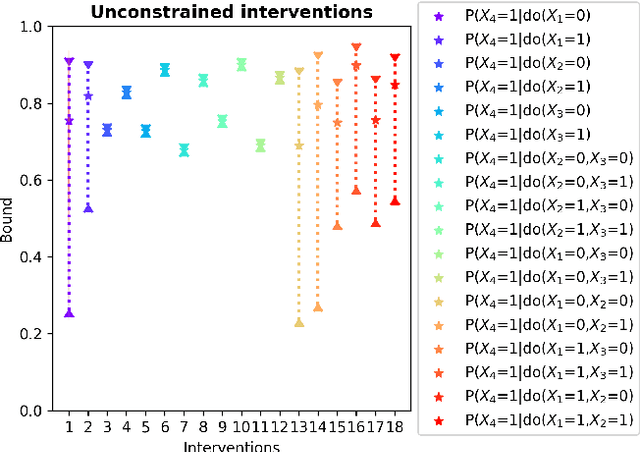
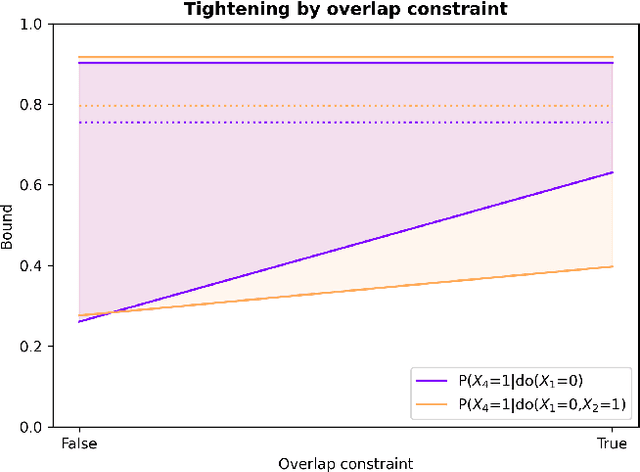
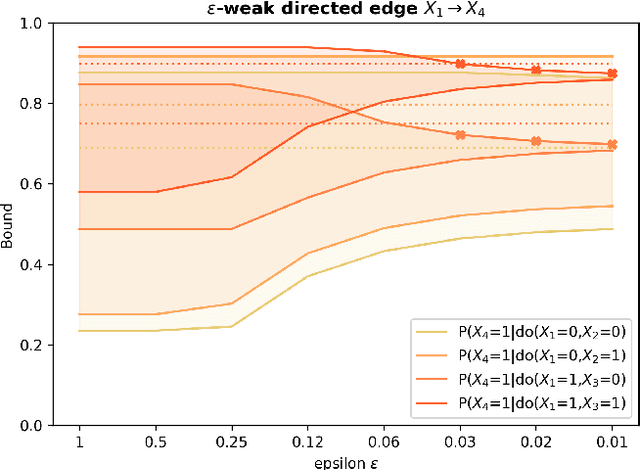
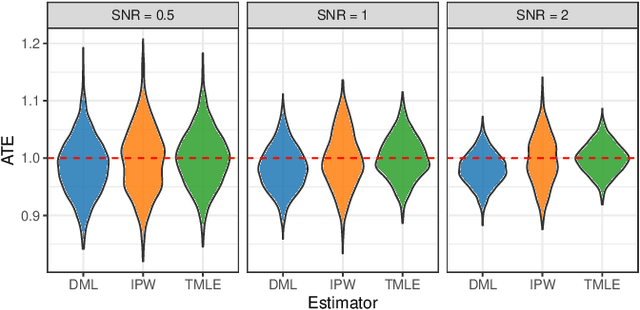
Due to unmeasured confounding, it is often not possible to identify causal effects from a postulated model. Nevertheless, we can ask for partial identification, which usually boils down to finding upper and lower bounds of a causal quantity of interest derived from all solutions compatible with the encoded structural assumptions. One appealing way to derive such bounds is by casting it in terms of a constrained optimization method that searches over all causal models compatible with evidence, as introduced in the classic work of Balke and Pearl (1994) for discrete data. Although by construction this guarantees tight bounds, it poses a formidable computational challenge. To cope with this issue, alternatives include algorithms that are not guaranteed to be tight, or by introducing restrictions on the class of models. In this paper, we introduce a novel alternative: inspired by ideas coming from belief propagation, we enforce compatibility between marginals of a causal model and data, without constructing a global causal model. We call this collection of locally consistent marginals the causal marginal polytope. As global independence constraints disappear when considering small dimensional tractable marginals, this also leads to a rethinking of how to elicit and express causal knowledge. We provide an explicit algorithm and implementation of this idea, and assess its practicality with numerical experiments.

Stochastic Causal Programming for Bounding Treatment Effects

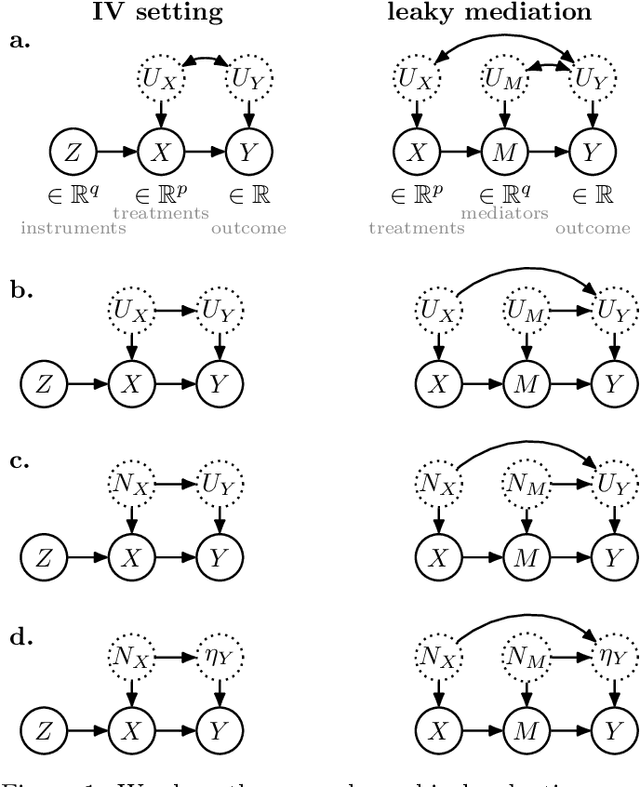
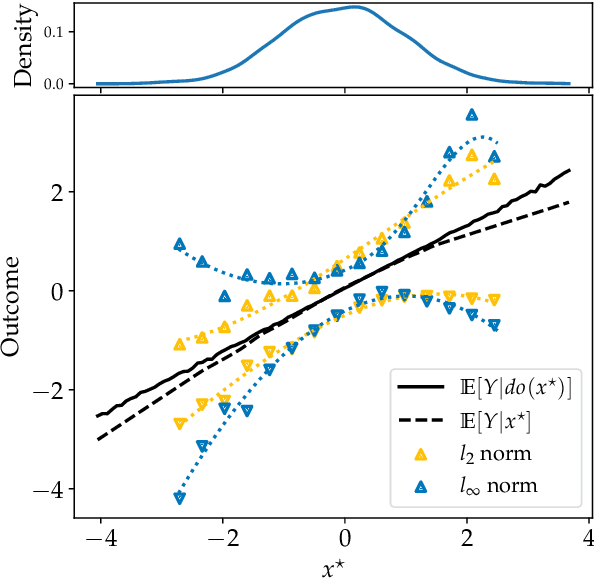
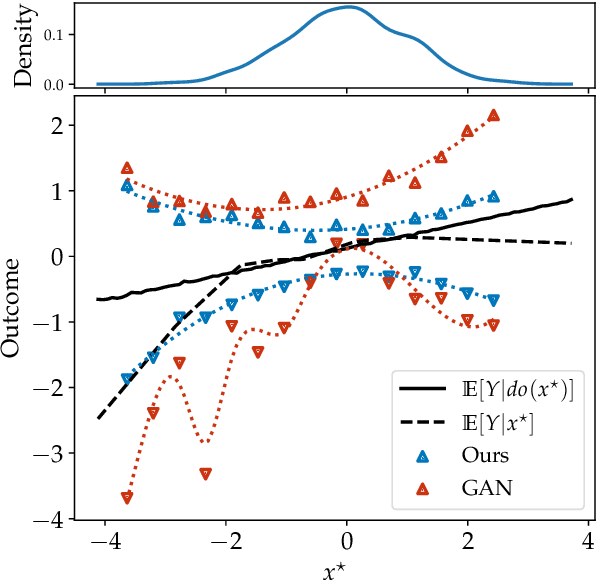
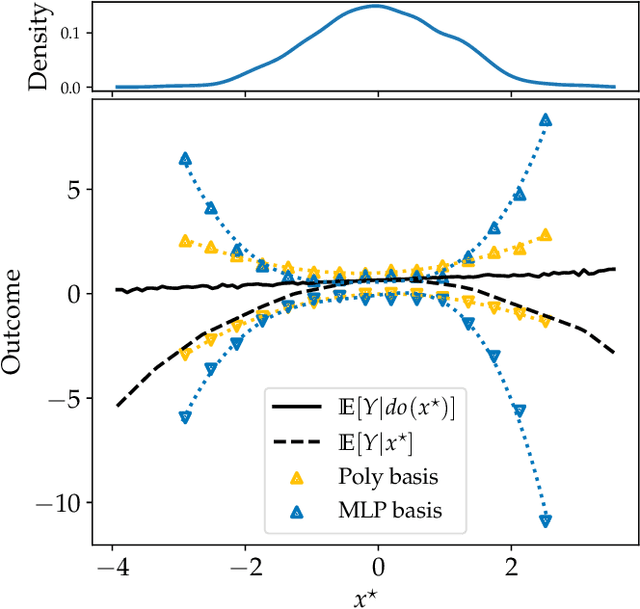
Causal effect estimation is important for numerous tasks in the natural and social sciences. However, identifying effects is impossible from observational data without making strong, often untestable assumptions. We consider algorithms for the partial identification problem, bounding treatment effects from multivariate, continuous treatments over multiple possible causal models when unmeasured confounding makes identification impossible. We consider a framework where observable evidence is matched to the implications of constraints encoded in a causal model by norm-based criteria. This generalizes classical approaches based purely on generative models. Casting causal effects as objective functions in a constrained optimization problem, we combine flexible learning algorithms with Monte Carlo methods to implement a family of solutions under the name of stochastic causal programming. In particular, we present ways by which such constrained optimization problems can be parameterized without likelihood functions for the causal or the observed data model, reducing the computational and statistical complexity of the task.

Questions for Flat-Minima Optimization of Modern Neural Networks

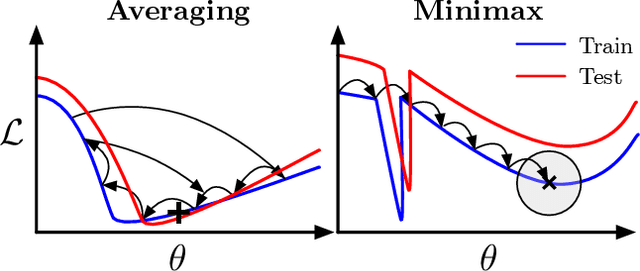
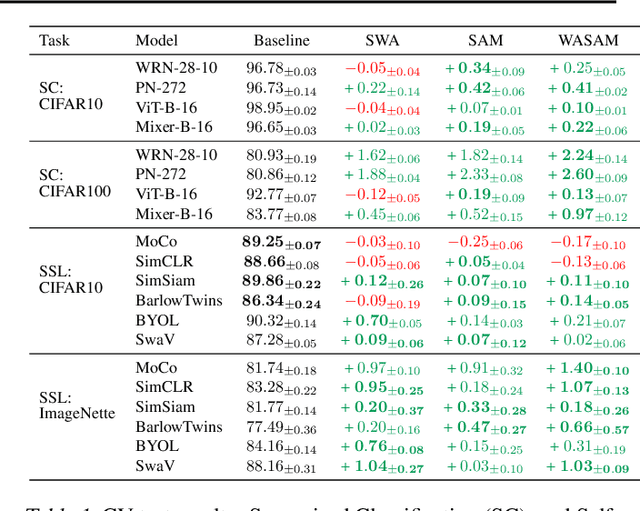
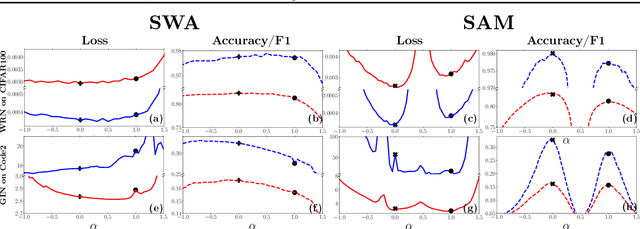
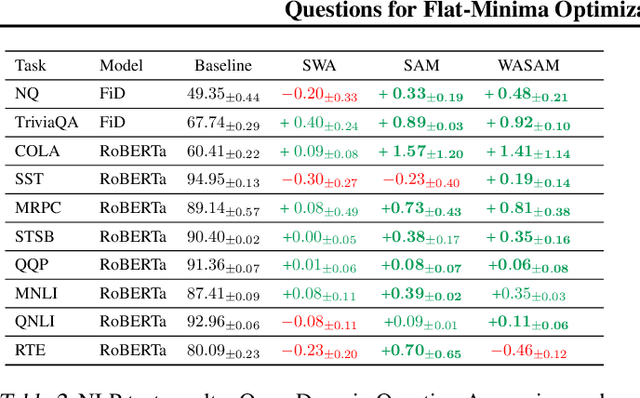
For training neural networks, flat-minima optimizers that seek to find parameters in neighborhoods having uniformly low loss (flat minima) have been shown to improve upon stochastic and adaptive gradient-based methods. Two methods for finding flat minima stand out: 1. Averaging methods (i.e., Stochastic Weight Averaging, SWA), and 2. Minimax methods (i.e., Sharpness Aware Minimization, SAM). However, despite similar motivations, there has been limited investigation into their properties and no comprehensive comparison between them. In this work, we investigate the loss surfaces from a systematic benchmarking of these approaches across computer vision, natural language processing, and graph learning tasks. The results lead to a simple hypothesis: since both approaches find different flat solutions, combining them should improve generalization even further. We verify this improves over either flat-minima approach in 39 out of 42 cases. When it does not, we investigate potential reasons. We hope our results across image, graph, and text data will help researchers to improve deep learning optimizers, and practitioners to pinpoint the optimizer for the problem at hand.

Graph Intervention Networks for Causal Effect Estimation

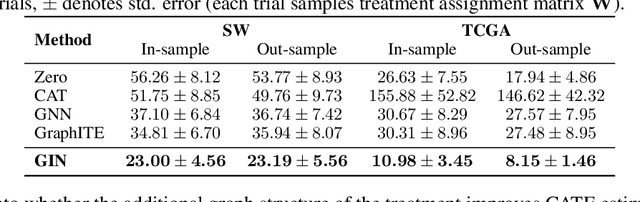
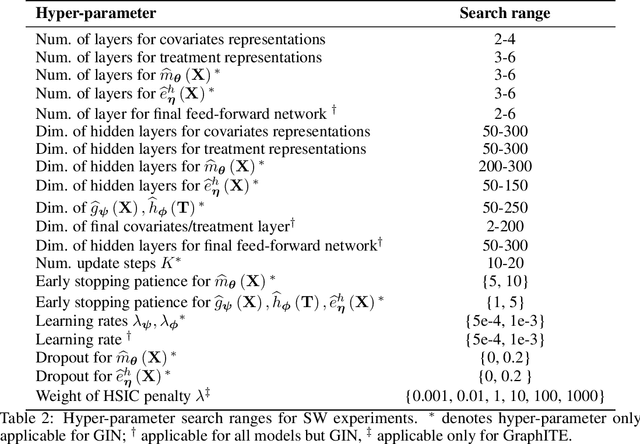
We address the estimation of conditional average treatment effects (CATEs) when treatments are graph-structured (e.g., molecular graphs of drugs). Given a weak condition on the effect, we propose a plug-in estimator that decomposes CATE estimation into separate, simpler optimization problems. Our estimator (a) isolates the causal estimands (reducing regularization bias), and (b) allows one to plug in arbitrary models for learning. In experiments with small-world and molecular graphs, we show that our approach outperforms prior approaches and is robust to varying selection biases. Our implementation is online.

Operationalizing Complex Causes: A Pragmatic View of Mediation

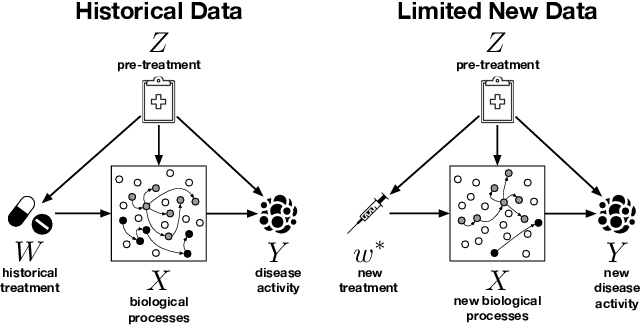
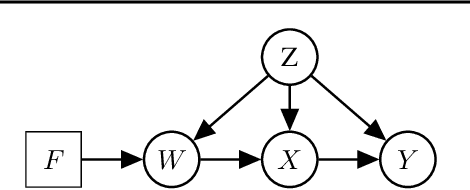
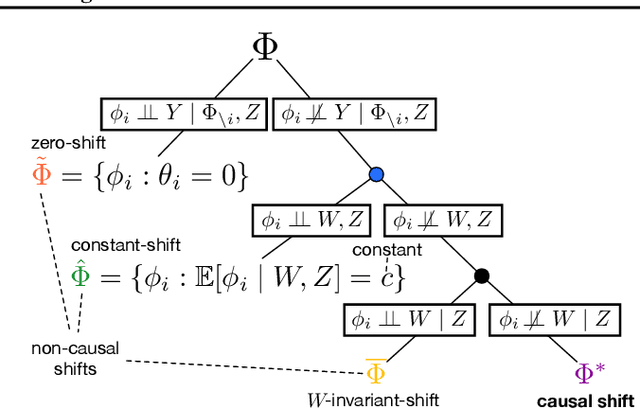
We examine the problem of causal response estimation for complex objects (e.g., text, images, genomics). In this setting, classical \emph{atomic} interventions are often not available (e.g., changes to characters, pixels, DNA base-pairs). Instead, we only have access to indirect or \emph{crude} interventions (e.g., enrolling in a writing program, modifying a scene, applying a gene therapy). In this work, we formalize this problem and provide an initial solution. Given a collection of candidate mediators, we propose (a) a two-step method for predicting the causal responses of crude interventions; and (b) a testing procedure to identify mediators of crude interventions. We demonstrate, on a range of simulated and real-world-inspired examples, that our approach allows us to efficiently estimate the effect of crude interventions with limited data from new treatment regimes.

Proximal Causal Learning with Kernels: Two-Stage Estimation and Moment Restriction

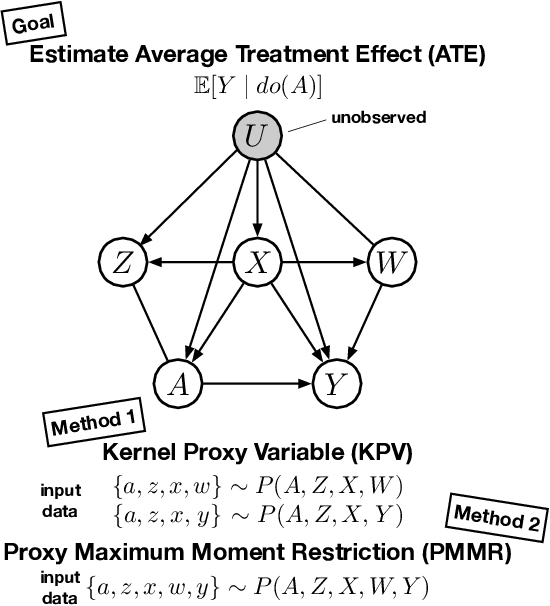
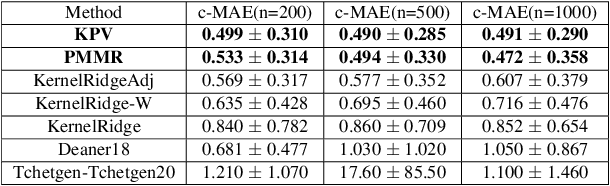
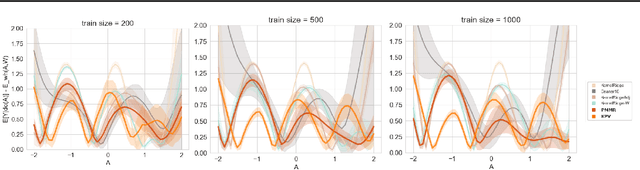
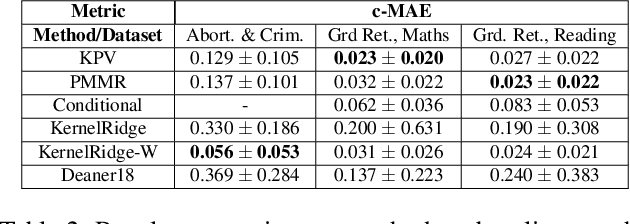
We address the problem of causal effect estimation in the presence of unobserved confounding, but where proxies for the latent confounder(s) are observed. We propose two kernel-based methods for nonlinear causal effect estimation in this setting: (a) a two-stage regression approach, and (b) a maximum moment restriction approach. We focus on the proximal causal learning setting, but our methods can be used to solve a wider class of inverse problems characterised by a Fredholm integral equation. In particular, we provide a unifying view of two-stage and moment restriction approaches for solving this problem in a nonlinear setting. We provide consistency guarantees for each algorithm, and we demonstrate these approaches achieve competitive results on synthetic data and data simulating a real-world task. In particular, our approach outperforms earlier methods that are not suited to leveraging proxy variables.

Learning Joint Nonlinear Effects from Single-variable Interventions in the Presence of Hidden Confounders

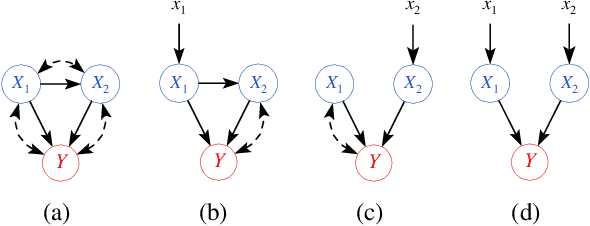
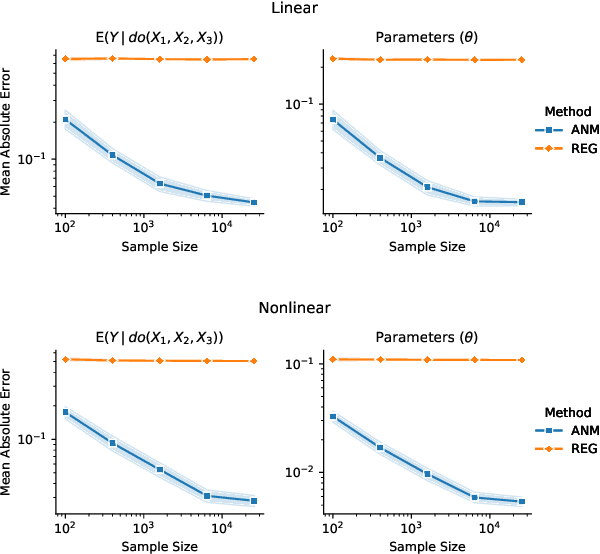
We propose an approach to estimate the effect of multiple simultaneous interventions in the presence of hidden confounders. To overcome the problem of hidden confounding, we consider the setting where we have access to not only the observational data but also sets of single-variable interventions in which each of the treatment variables is intervened on separately. We prove identifiability under the assumption that the data is generated from a nonlinear continuous structural causal model with additive Gaussian noise. In addition, we propose a simple parameter estimation method by pooling all the data from different regimes and jointly maximizing the combined likelihood. We also conduct comprehensive experiments to verify the identifiability result as well as to compare the performance of our approach against a baseline on both synthetic and real-world data.

A Class of Algorithms for General Instrumental Variable Models

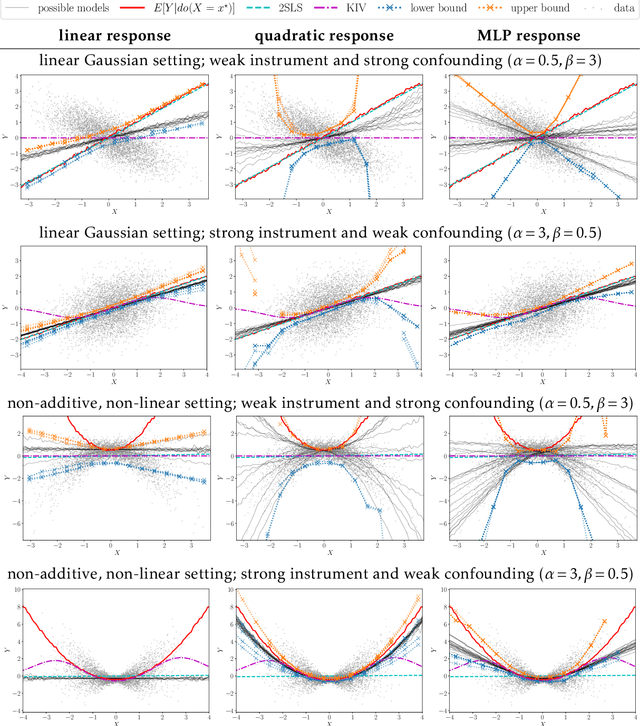
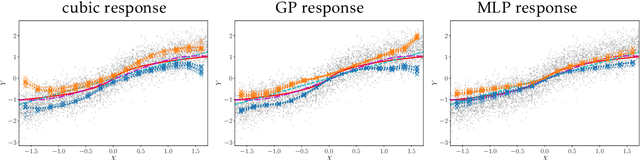
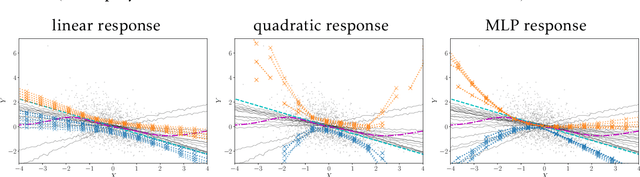
Causal treatment effect estimation is a key problem that arises in a variety of real-world settings, from personalized medicine to governmental policy making. There has been a flurry of recent work in machine learning on estimating causal effects when one has access to an instrument. However, to achieve identifiability, they in general require one-size-fits-all assumptions such as an additive error model for the outcome. An alternative is partial identification, which provides bounds on the causal effect. Little exists in terms of bounding methods that can deal with the most general case, where the treatment itself can be continuous. Moreover, bounding methods generally do not allow for a continuum of assumptions on the shape of the causal effect that can smoothly trade off stronger background knowledge for more informative bounds. In this work, we provide a method for causal effect bounding in continuous distributions, leveraging recent advances in gradient-based methods for the optimization of computationally intractable objective functions. We demonstrate on a set of synthetic and real-world data that our bounds capture the causal effect when additive methods fail, providing a useful range of answers compatible with observation as opposed to relying on unwarranted structural assumptions.

Differentiable Causal Backdoor Discovery

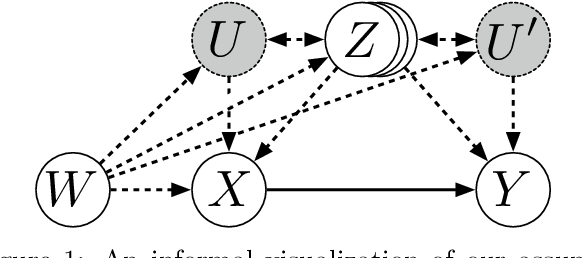
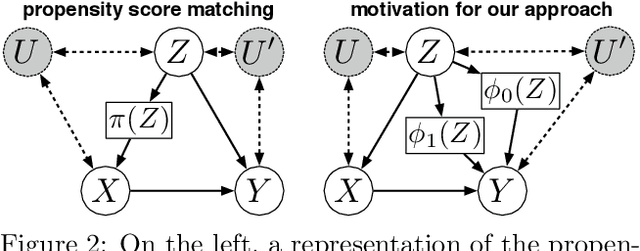
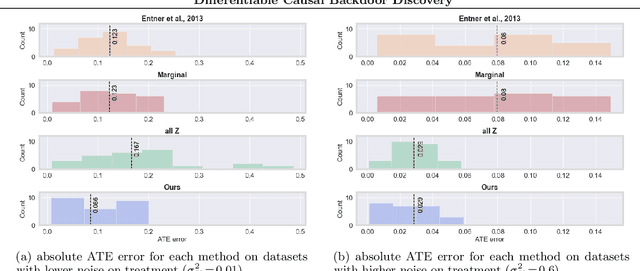
Discovering the causal effect of a decision is critical to nearly all forms of decision-making. In particular, it is a key quantity in drug development, in crafting government policy, and when implementing a real-world machine learning system. Given only observational data, confounders often obscure the true causal effect. Luckily, in some cases, it is possible to recover the causal effect by using certain observed variables to adjust for the effects of confounders. However, without access to the true causal model, finding this adjustment requires brute-force search. In this work, we present an algorithm that exploits auxiliary variables, similar to instruments, in order to find an appropriate adjustment by a gradient-based optimization method. We demonstrate that it outperforms practical alternatives in estimating the true causal effect, without knowledge of the full causal graph.