SPD Learning for Covariance-Based Neuroimaging Analysis: Perspectives, Methods, and Challenges

Neuroimaging provides a critical framework for characterizing brain activity by quantifying connectivity patterns and functional architecture across modalities. While modern machine learning has significantly advanced our understanding of neural processing mechanisms through these datasets, decoding task-specific signatures must contend with inherent neuroimaging constraints, for example, low signal-to-noise ratios in raw electrophysiological recordings, cross-session non-stationarity, and limited sample sizes. This review focuses on machine learning approaches for covariance-based neuroimaging data, where often symmetric positive definite (SPD) matrices under full-rank conditions encode inter-channel relationships. By equipping the space of SPD matrices with Riemannian metrics (e.g., affine-invariant or log-Euclidean), their space forms a Riemannian manifold enabling geometric analysis. We unify methodologies operating on this manifold under the SPD learning framework, which systematically leverages the SPD manifold's geometry to process covariance features, thereby advancing brain imaging analytics.

On the interpretation of linear Riemannian tangent space model parameters in M/EEG

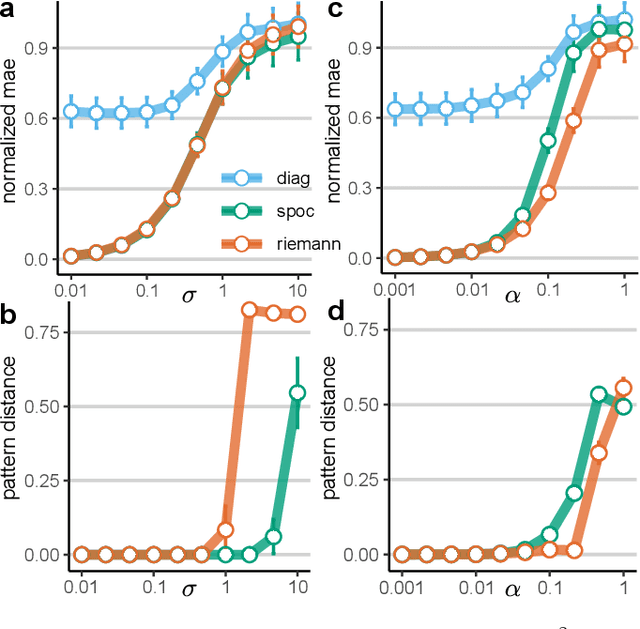
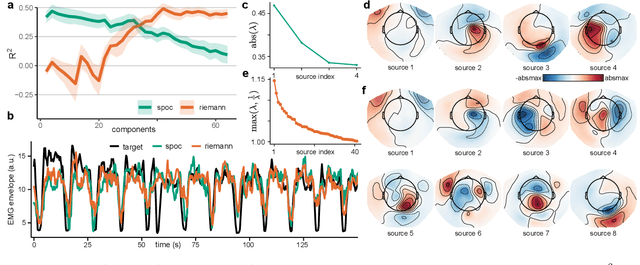
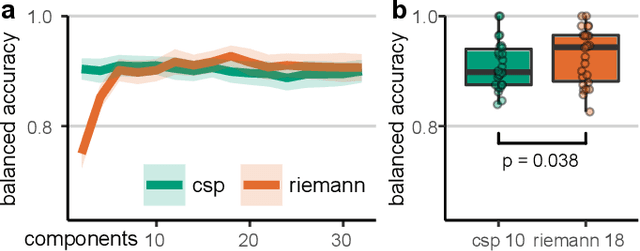
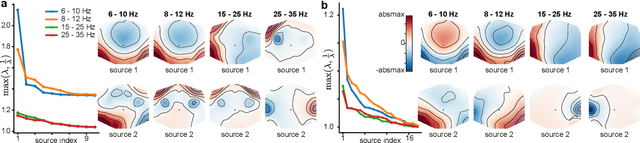
Riemannian tangent space methods offer state-of-the-art performance in magnetoencephalography (MEG) and electroencephalography (EEG) based applications such as brain-computer interfaces and biomarker development. One limitation, particularly relevant for biomarker development, is limited model interpretability compared to established component-based methods. Here, we propose a method to transform the parameters of linear tangent space models into interpretable patterns. Using typical assumptions, we show that this approach identifies the true patterns of latent sources, encoding a target signal. In simulations and two real MEG and EEG datasets, we demonstrate the validity of the proposed approach and investigate its behavior when the model assumptions are violated. Our results confirm that Riemannian tangent space methods are robust to differences in the source patterns across observations. We found that this robustness property also transfers to the associated patterns.