Robustness of graph embedding methods for community detection

This study investigates the robustness of graph embedding methods for community detection in the face of network perturbations, specifically edge deletions. Graph embedding techniques, which represent nodes as low-dimensional vectors, are widely used for various graph machine learning tasks due to their ability to capture structural properties of networks effectively. However, the impact of perturbations on the performance of these methods remains relatively understudied. The research considers state-of-the-art graph embedding methods from two families: matrix factorization (e.g., LE, LLE, HOPE, M-NMF) and random walk-based (e.g., DeepWalk, LINE, node2vec). Through experiments conducted on both synthetic and real-world networks, the study reveals varying degrees of robustness within each family of graph embedding methods. The robustness is found to be influenced by factors such as network size, initial community partition strength, and the type of perturbation. Notably, node2vec and LLE consistently demonstrate higher robustness for community detection across different scenarios, including networks with degree and community size heterogeneity. These findings highlight the importance of selecting an appropriate graph embedding method based on the specific characteristics of the network and the task at hand, particularly in scenarios where robustness to perturbations is crucial.

Reinforcement Learning as a Parsimonious Alternative to Prediction Cascades: A Case Study on Image Segmentation

Deep learning architectures have achieved state-of-the-art (SOTA) performance on computer vision tasks such as object detection and image segmentation. This may be attributed to the use of over-parameterized, monolithic deep learning architectures executed on large datasets. Although such architectures lead to increased accuracy, this is usually accompanied by a large increase in computation and memory requirements during inference. While this is a non-issue in traditional machine learning pipelines, the recent confluence of machine learning and fields like the Internet of Things has rendered such large architectures infeasible for execution in low-resource settings. In such settings, previous efforts have proposed decision cascades where inputs are passed through models of increasing complexity until desired performance is achieved. However, we argue that cascaded prediction leads to increased computational cost due to wasteful intermediate computations. To address this, we propose PaSeR (Parsimonious Segmentation with Reinforcement Learning) a non-cascading, cost-aware learning pipeline as an alternative to cascaded architectures. Through experimental evaluation on real-world and standard datasets, we demonstrate that PaSeR achieves better accuracy while minimizing computational cost relative to cascaded models. Further, we introduce a new metric IoU/GigaFlop to evaluate the balance between cost and performance. On the real-world task of battery material phase segmentation, PaSeR yields a minimum performance improvement of 174% on the IoU/GigaFlop metric with respect to baselines. We also demonstrate PaSeR's adaptability to complementary models trained on a noisy MNIST dataset, where it achieved a minimum performance improvement on IoU/GigaFlop of 13.4% over SOTA models. Code and data are available at https://github.com/scailab/paser .

Outlier Detection for Text Data : An Extended Version

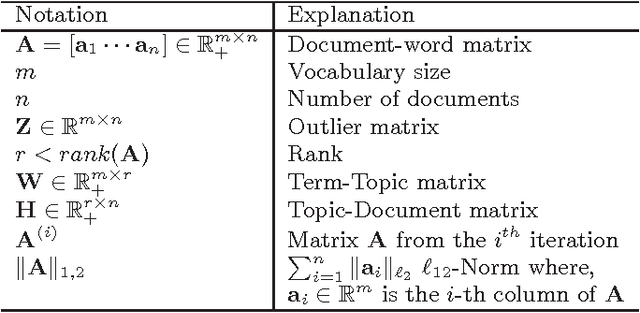
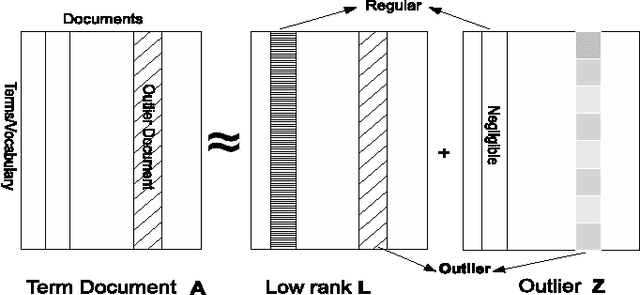
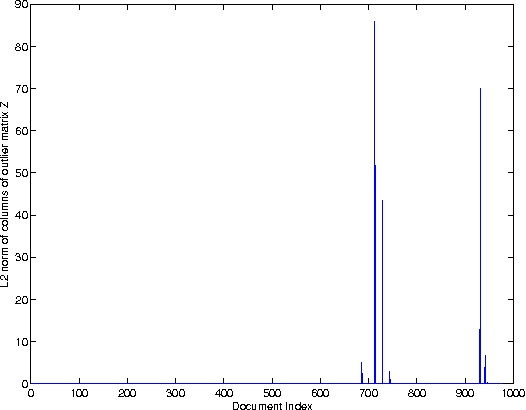
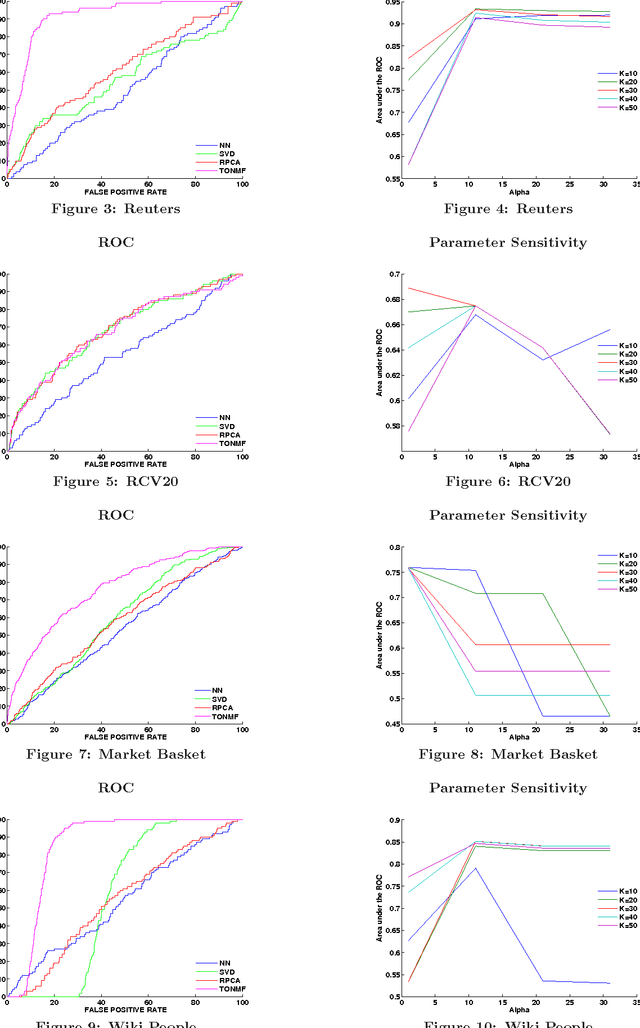
The problem of outlier detection is extremely challenging in many domains such as text, in which the attribute values are typically non-negative, and most values are zero. In such cases, it often becomes difficult to separate the outliers from the natural variations in the patterns in the underlying data. In this paper, we present a matrix factorization method, which is naturally able to distinguish the anomalies with the use of low rank approximations of the underlying data. Our iterative algorithm TONMF is based on block coordinate descent (BCD) framework. We define blocks over the term-document matrix such that the function becomes solvable. Given most recently updated values of other matrix blocks, we always update one block at a time to its optimal. Our approach has significant advantages over traditional methods for text outlier detection. Finally, we present experimental results illustrating the effectiveness of our method over competing methods.

MPI-FAUN: An MPI-Based Framework for Alternating-Updating Nonnegative Matrix Factorization

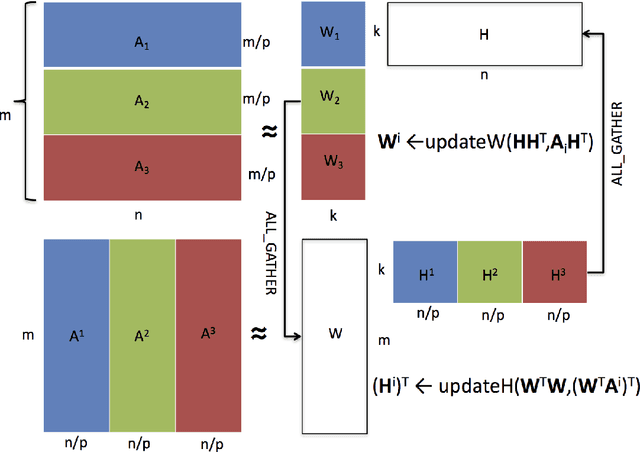
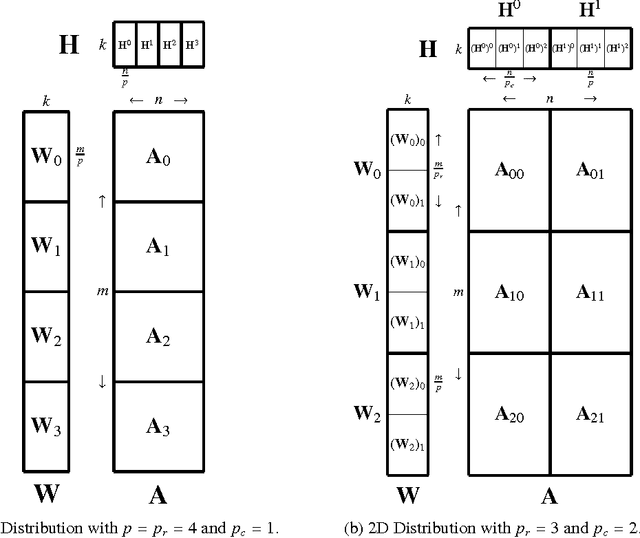
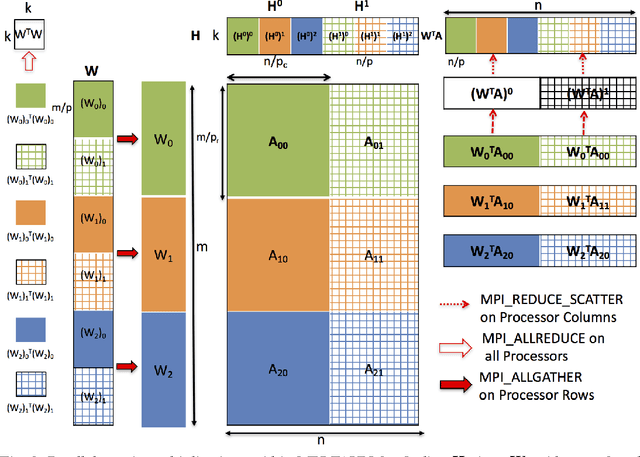
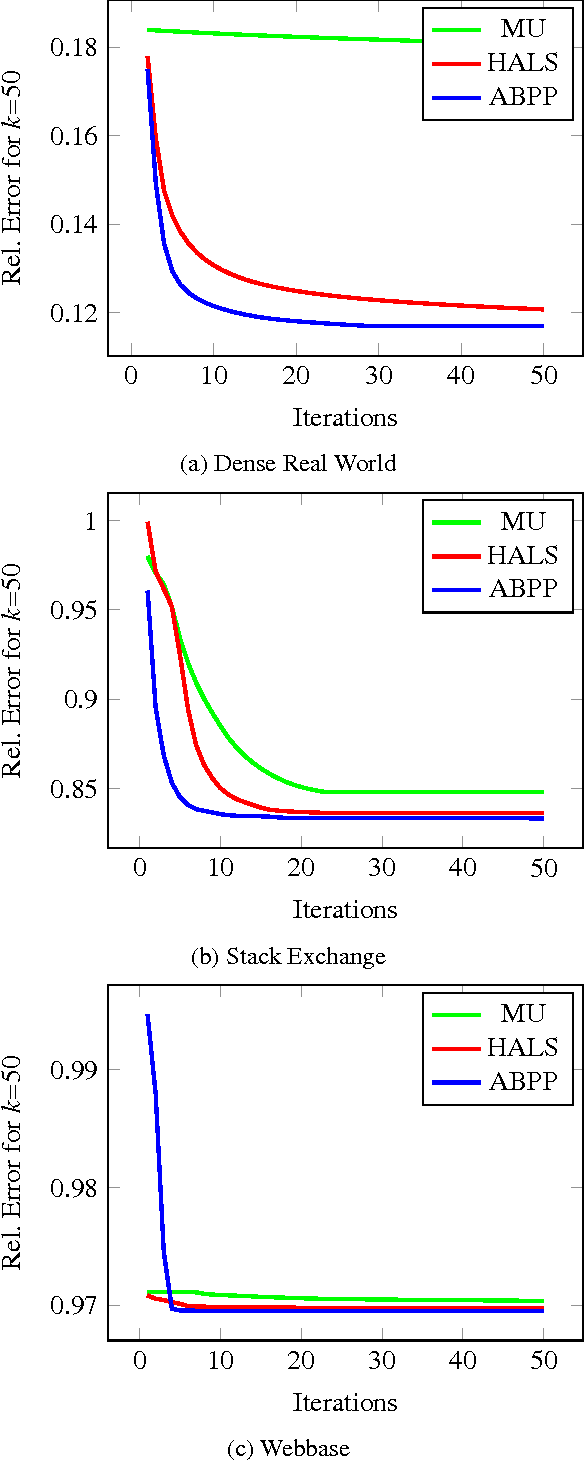
Non-negative matrix factorization (NMF) is the problem of determining two non-negative low rank factors $W$ and $H$, for the given input matrix $A$, such that $A \approx W H$. NMF is a useful tool for many applications in different domains such as topic modeling in text mining, background separation in video analysis, and community detection in social networks. Despite its popularity in the data mining community, there is a lack of efficient parallel algorithms to solve the problem for big data sets. The main contribution of this work is a new, high-performance parallel computational framework for a broad class of NMF algorithms that iteratively solves alternating non-negative least squares (NLS) subproblems for $W$ and $H$. It maintains the data and factor matrices in memory (distributed across processors), uses MPI for interprocessor communication, and, in the dense case, provably minimizes communication costs (under mild assumptions). The framework is flexible and able to leverage a variety of NMF and NLS algorithms, including Multiplicative Update, Hierarchical Alternating Least Squares, and Block Principal Pivoting. Our implementation allows us to benchmark and compare different algorithms on massive dense and sparse data matrices of size that spans for few hundreds of millions to billions. We demonstrate the scalability of our algorithm and compare it with baseline implementations, showing significant performance improvements. The code and the datasets used for conducting the experiments are available online.