Randomized Algorithms for Symmetric Nonnegative Matrix Factorization

Symmetric Nonnegative Matrix Factorization (SymNMF) is a technique in data analysis and machine learning that approximates a symmetric matrix with a product of a nonnegative, low-rank matrix and its transpose. To design faster and more scalable algorithms for SymNMF we develop two randomized algorithms for its computation. The first algorithm uses randomized matrix sketching to compute an initial low-rank input matrix and proceeds to use this input to rapidly compute a SymNMF. The second algorithm uses randomized leverage score sampling to approximately solve constrained least squares problems. Many successful methods for SymNMF rely on (approximately) solving sequences of constrained least squares problems. We prove theoretically that leverage score sampling can approximately solve nonnegative least squares problems to a chosen accuracy with high probability. Finally we demonstrate that both methods work well in practice by applying them to graph clustering tasks on large real world data sets. These experiments show that our methods approximately maintain solution quality and achieve significant speed ups for both large dense and large sparse problems.

WellFactor: Patient Profiling using Integrative Embedding of Healthcare Data

In the rapidly evolving healthcare industry, platforms now have access to not only traditional medical records, but also diverse data sets encompassing various patient interactions, such as those from healthcare web portals. To address this rich diversity of data, we introduce WellFactor: a method that derives patient profiles by integrating information from these sources. Central to our approach is the utilization of constrained low-rank approximation. WellFactor is optimized to handle the sparsity that is often inherent in healthcare data. Moreover, by incorporating task-specific label information, our method refines the embedding results, offering a more informed perspective on patients. One important feature of WellFactor is its ability to compute embeddings for new, previously unobserved patient data instantaneously, eliminating the need to revisit the entire data set or recomputing the embedding. Comprehensive evaluations on real-world healthcare data demonstrate WellFactor's effectiveness. It produces better results compared to other existing methods in classification performance, yields meaningful clustering of patients, and delivers consistent results in patient similarity searches and predictions.

Patient Clustering via Integrated Profiling of Clinical and Digital Data

We introduce a novel profile-based patient clustering model designed for clinical data in healthcare. By utilizing a method grounded on constrained low-rank approximation, our model takes advantage of patients' clinical data and digital interaction data, including browsing and search, to construct patient profiles. As a result of the method, nonnegative embedding vectors are generated, serving as a low-dimensional representation of the patients. Our model was assessed using real-world patient data from a healthcare web portal, with a comprehensive evaluation approach which considered clustering and recommendation capabilities. In comparison to other baselines, our approach demonstrated superior performance in terms of clustering coherence and recommendation accuracy.

Skew-Symmetric Adjacency Matrices for Clustering Directed Graphs

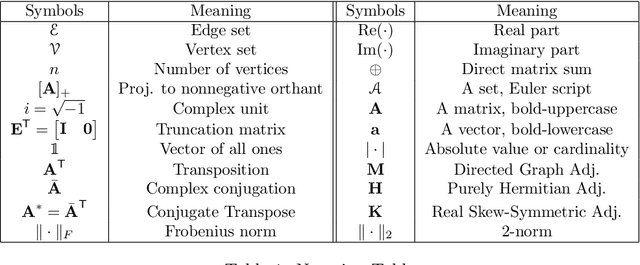
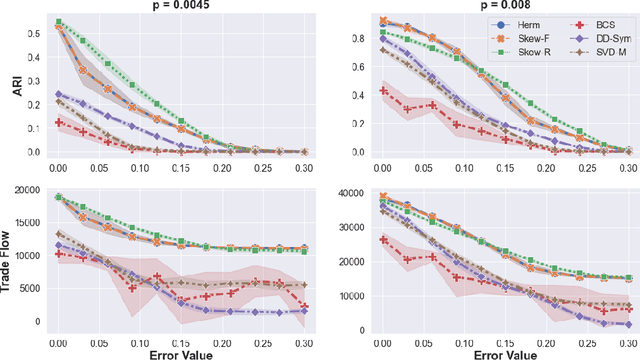
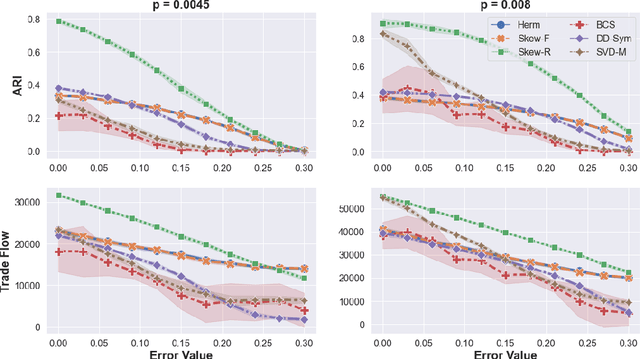
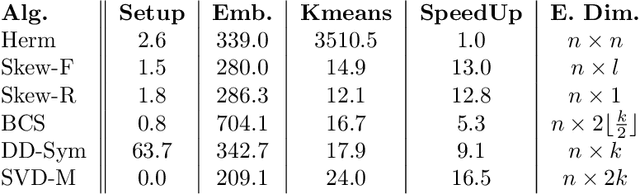
Cut-based directed graph (digraph) clustering often focuses on finding dense within-cluster or sparse between-cluster connections, similar to cut-based undirected graph clustering methods. In contrast, for flow-based clusterings the edges between clusters tend to be oriented in one direction and have been found in migration data, food webs, and trade data. In this paper we introduce a spectral algorithm for finding flow-based clusterings. The proposed algorithm is based on recent work which uses complex-valued Hermitian matrices to represent digraphs. By establishing an algebraic relationship between a complex-valued Hermitian representation and an associated real-valued, skew-symmetric matrix the proposed algorithm produces clusterings while remaining completely in the real field. Our algorithm uses less memory and asymptotically less computation while provably preserving solution quality. We also show the algorithm can be easily implemented using standard computational building blocks, possesses better numerical properties, and loans itself to a natural interpretation via an objective function relaxation argument.

SWIFT: Scalable Wasserstein Factorization for Sparse Nonnegative Tensors

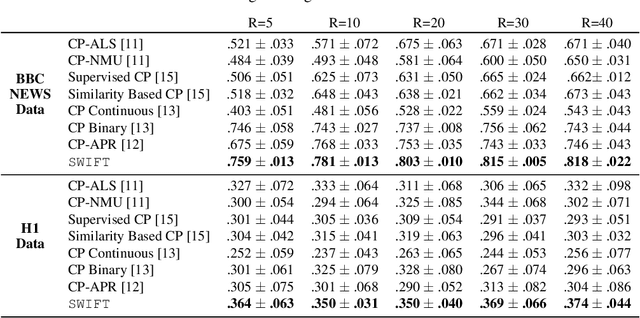
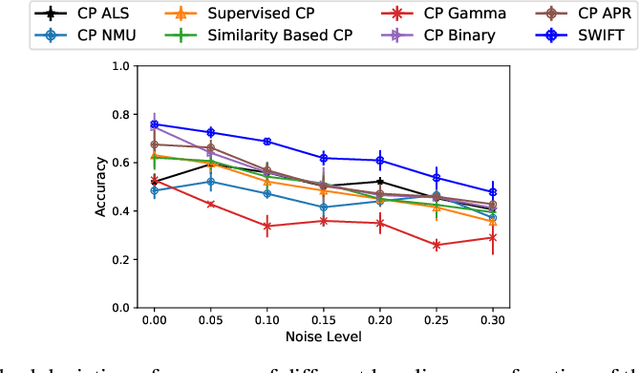
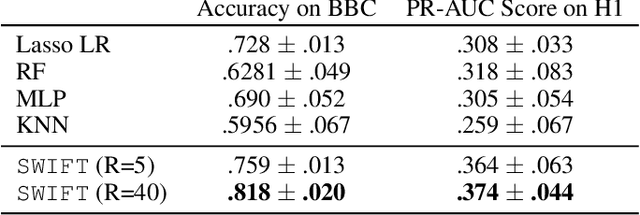
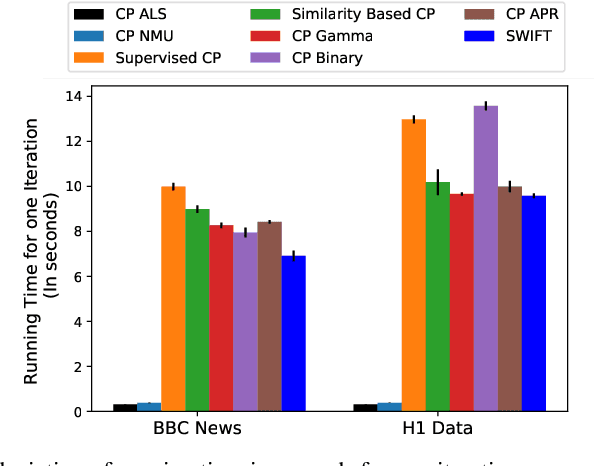
Existing tensor factorization methods assume that the input tensor follows some specific distribution (i.e. Poisson, Bernoulli and Gaussian), and solve the factorization by minimizing some empirical loss functions defined based on the corresponding distribution. However, it suffers from several drawbacks: 1) In reality, the underlying distributions are complicated and unknown, making it infeasible to be approximated by a simple distribution. 2) The correlation across dimensions of the input tensor is not well utilized, leading to sub-optimal performance. Although heuristics were proposed to incorporate such correlation as side information under Gaussian distribution, they can not easily be generalized to other distributions. Thus, a more principled way of utilizing the correlation in tensor factorization models is still an open challenge. Without assuming any explicit distribution, we formulate the tensor factorization as an optimal transport problem with Wasserstein distance, which can handle non-negative inputs. We introduce SWIFT, which minimizes the Wasserstein distance that measures the distance between the input tensor and that of the reconstruction. In particular, we define the N-th order tensor Wasserstein loss for the widely used tensor CP factorization, and derive the optimization algorithm that minimizes it. By leveraging sparsity structure and different equivalent formulations for optimizing computational efficiency, SWIFT is as scalable as other well-known CP algorithms. Using the factor matrices as features, SWIFT achieves up to 9.65% and 11.31% relative improvement over baselines for downstream prediction tasks. Under the noisy conditions, SWIFT achieves up to 15% and 17% relative improvements over the best competitors for the prediction tasks.

Hypergraph Random Walks, Laplacians, and Clustering

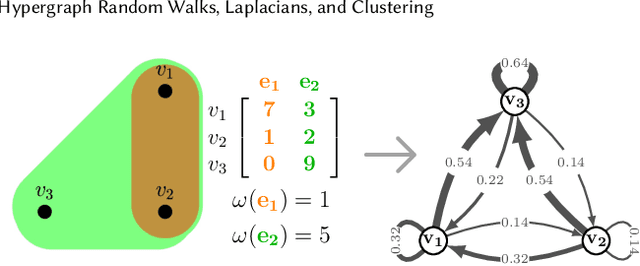
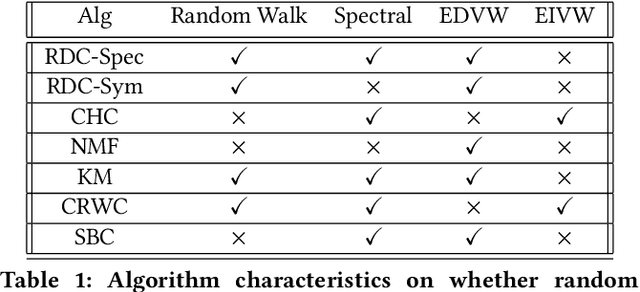
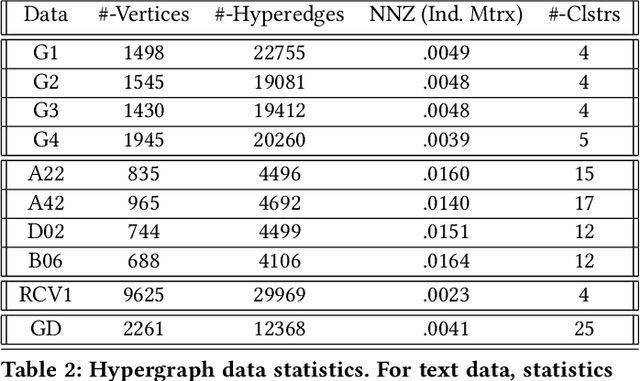
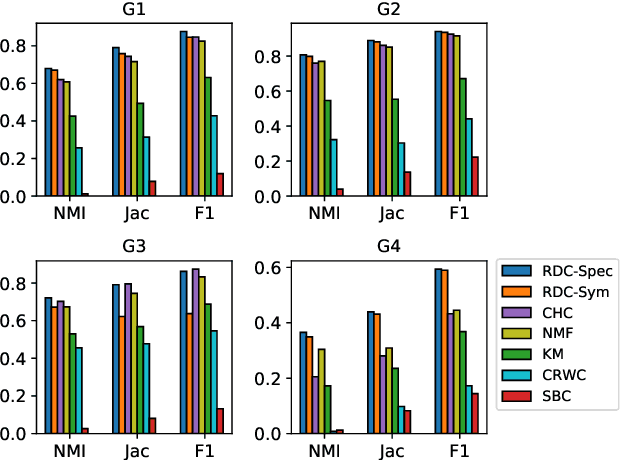
We propose a flexible framework for clustering hypergraph-structured data based on recently proposed random walks utilizing edge-dependent vertex weights. When incorporating edge-dependent vertex weights (EDVW), a weight is associated with each vertex-hyperedge pair, yielding a weighted incidence matrix of the hypergraph. Such weightings have been utilized in term-document representations of text data sets. We explain how random walks with EDVW serve to construct different hypergraph Laplacian matrices, and then develop a suite of clustering methods that use these incidence matrices and Laplacians for hypergraph clustering. Using several data sets from real-life applications, we compare the performance of these clustering algorithms experimentally against a variety of existing hypergraph clustering methods. We show that the proposed methods produce higher-quality clusters and conclude by highlighting avenues for future work.

TASTE: Temporal and Static Tensor Factorization for Phenotyping Electronic Health Records

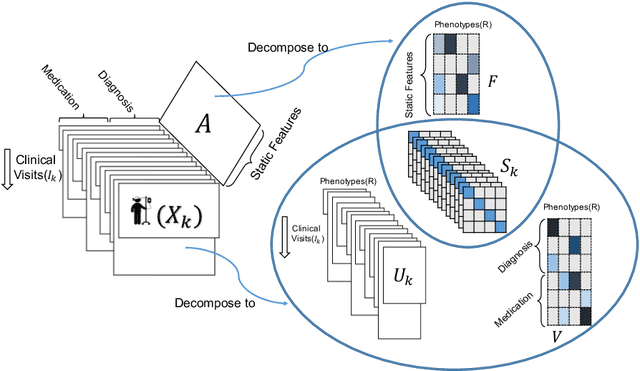
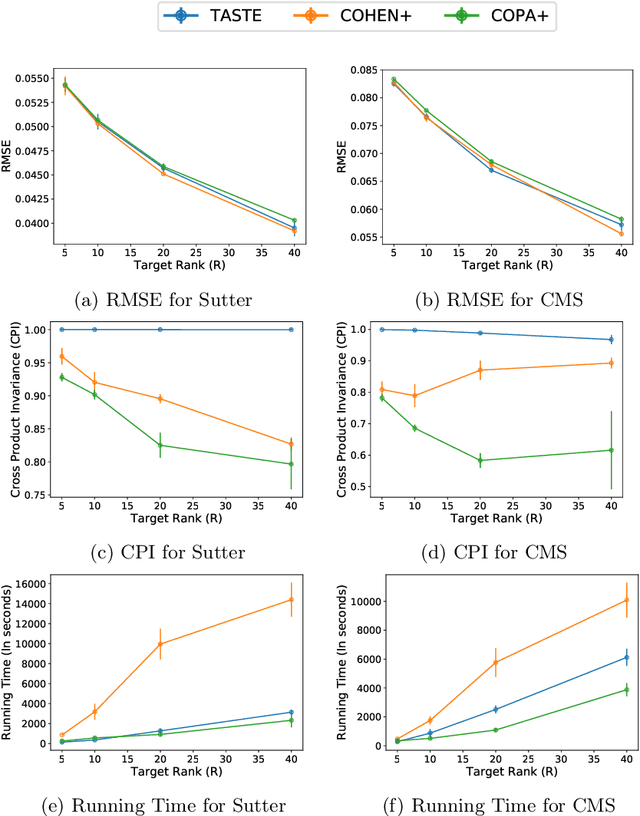
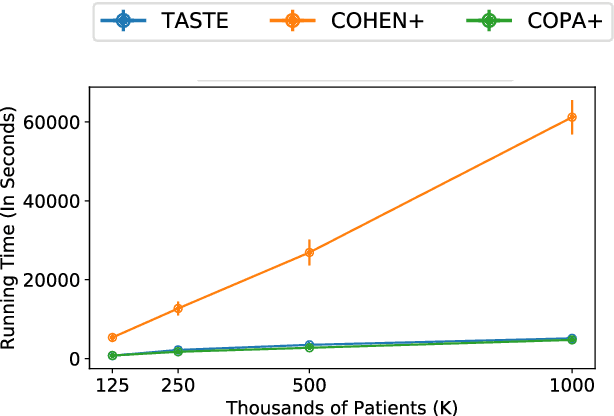
Phenotyping electronic health records (EHR) focuses on defining meaningful patient groups (e.g., heart failure group and diabetes group) and identifying the temporal evolution of patients in those groups. Tensor factorization has been an effective tool for phenotyping. Most of the existing works assume either a static patient representation with aggregate data or only model temporal data. However, real EHR data contain both temporal (e.g., longitudinal clinical visits) and static information (e.g., patient demographics), which are difficult to model simultaneously. In this paper, we propose Temporal And Static TEnsor factorization (TASTE) that jointly models both static and temporal information to extract phenotypes. TASTE combines the PARAFAC2 model with non-negative matrix factorization to model a temporal and a static tensor. To fit the proposed model, we transform the original problem into simpler ones which are optimally solved in an alternating fashion. For each of the sub-problems, our proposed mathematical reformulations lead to efficient sub-problem solvers. Comprehensive experiments on large EHR data from a heart failure (HF) study confirmed that TASTE is up to 14x faster than several baselines and the resulting phenotypes were confirmed to be clinically meaningful by a cardiologist. Using 80 phenotypes extracted by TASTE, a simple logistic regression can achieve the same level of area under the curve (AUC) for HF prediction compared to a deep learning model using recurrent neural networks (RNN) with 345 features.

Learning Joint Gaussian Representations for Movies, Actors, and Literary Characters

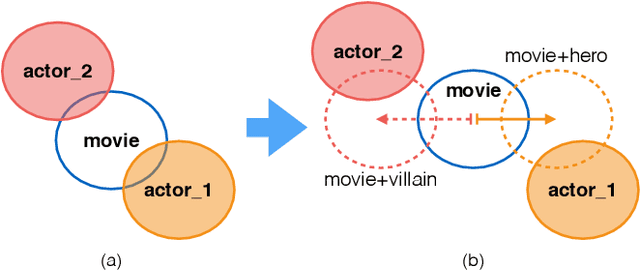
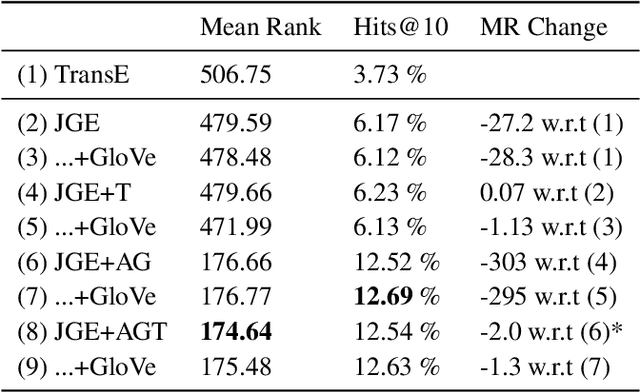
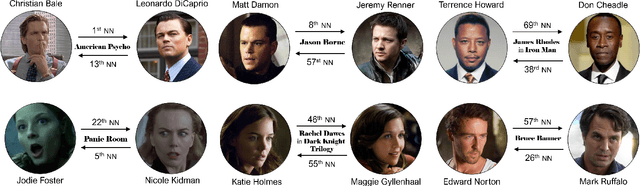
Understanding of narrative content has become an increasingly popular topic. However, narrative semantics pose difficult challenges as the effects of multiple narrative facets, such as the text, events, character types, and genres, are tightly intertwined. We present a joint representation learning framework for embedding actors, literary characters, movies, genres, and descriptive keywords as Gaussian distributions and translation vectors on the Gaussian means. The Gaussian variance naturally corresponds to actors' versatility, a central concept in acting. Our estimate of actors' versatility agree with domain experts' rankings 65.95% of the time. This is, to our knowledge, the first computational technique for estimating this semantic concept. Additionally, the model substantially outperforms a TransE baseline in prediction of actor casting choices.

SUSTain: Scalable Unsupervised Scoring for Tensors and its Application to Phenotyping

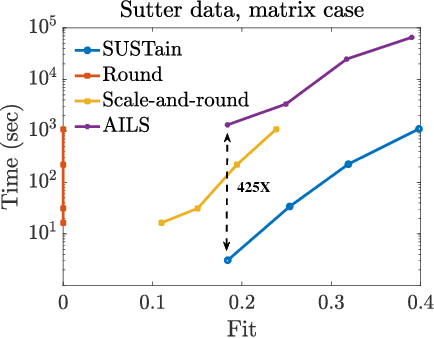
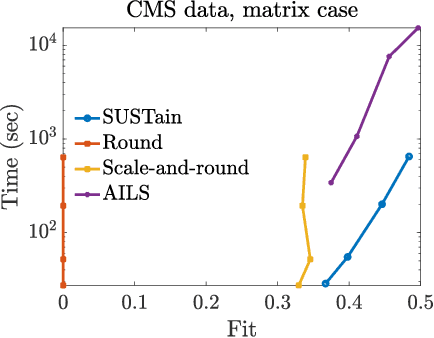
This paper presents a new method, which we call SUSTain, that extends real-valued matrix and tensor factorizations to data where values are integers. Such data are common when the values correspond to event counts or ordinal measures. The conventional approach is to treat integer data as real, and then apply real-valued factorizations. However, doing so fails to preserve important characteristics of the original data, thereby making it hard to interpret the results. Instead, our approach extracts factor values from integer datasets as scores that are constrained to take values from a small integer set. These scores are easy to interpret: a score of zero indicates no feature contribution and higher scores indicate distinct levels of feature importance. At its core, SUSTain relies on: a) a problem partitioning into integer-constrained subproblems, so that they can be optimally solved in an efficient manner; and b) organizing the order of the subproblems' solution, to promote reuse of shared intermediate results. We propose two variants, SUSTain_M and SUSTain_T, to handle both matrix and tensor inputs, respectively. We evaluate SUSTain against several state-of-the-art baselines on both synthetic and real Electronic Health Record (EHR) datasets. Comparing to those baselines, SUSTain shows either significantly better fit or orders of magnitude speedups that achieve a comparable fit (up to 425X faster). We apply SUSTain to EHR datasets to extract patient phenotypes (i.e., clinically meaningful patient clusters). Furthermore, 87% of them were validated as clinically meaningful phenotypes related to heart failure by a cardiologist.

Hybrid Clustering based on Content and Connection Structure using Joint Nonnegative Matrix Factorization

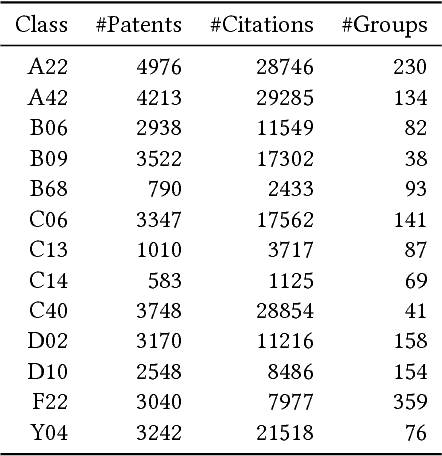
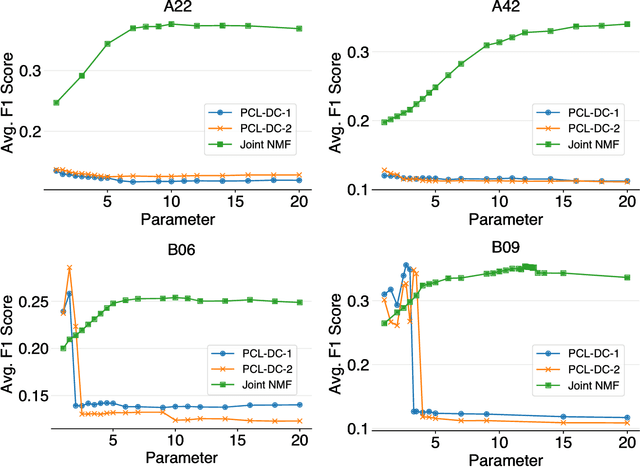
We present a hybrid method for latent information discovery on the data sets containing both text content and connection structure based on constrained low rank approximation. The new method jointly optimizes the Nonnegative Matrix Factorization (NMF) objective function for text clustering and the Symmetric NMF (SymNMF) objective function for graph clustering. We propose an effective algorithm for the joint NMF objective function, based on a block coordinate descent (BCD) framework. The proposed hybrid method discovers content associations via latent connections found using SymNMF. The method can also be applied with a natural conversion of the problem when a hypergraph formulation is used or the content is associated with hypergraph edges. Experimental results show that by simultaneously utilizing both content and connection structure, our hybrid method produces higher quality clustering results compared to the other NMF clustering methods that uses content alone (standard NMF) or connection structure alone (SymNMF). We also present some interesting applications to several types of real world data such as citation recommendations of papers. The hybrid method proposed in this paper can also be applied to general data expressed with both feature space vectors and pairwise similarities and can be extended to the case with multiple feature spaces or multiple similarity measures.