Strengthening Deterministic Policies for POMDPs

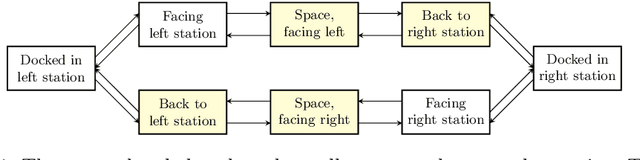
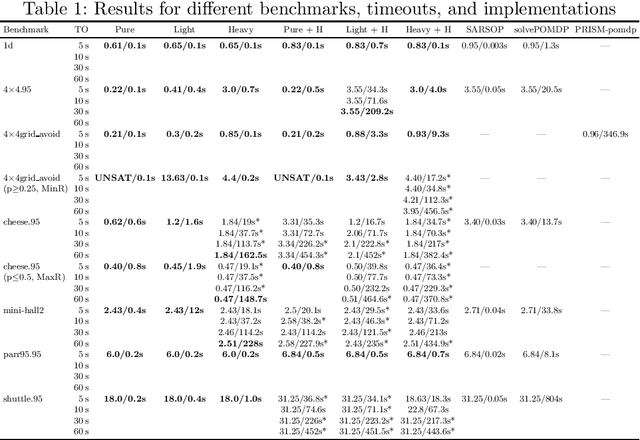
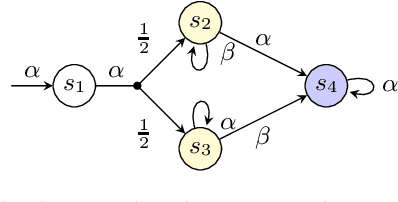
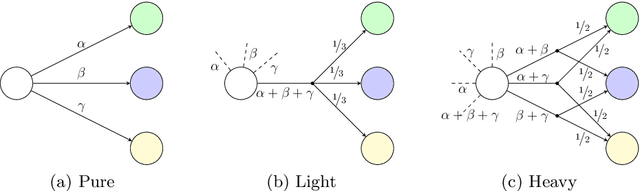
The synthesis problem for partially observable Markov decision processes (POMDPs) is to compute a policy that satisfies a given specification. Such policies have to take the full execution history of a POMDP into account, rendering the problem undecidable in general. A common approach is to use a limited amount of memory and randomize over potential choices. Yet, this problem is still NP-hard and often computationally intractable in practice. A restricted problem is to use neither history nor randomization, yielding policies that are called stationary and deterministic. Previous approaches to compute such policies employ mixed-integer linear programming (MILP). We provide a novel MILP encoding that supports sophisticated specifications in the form of temporal logic constraints. It is able to handle an arbitrary number of such specifications. Yet, randomization and memory are often mandatory to achieve satisfactory policies. First, we extend our encoding to deliver a restricted class of randomized policies. Second, based on the results of the original MILP, we employ a preprocessing of the POMDP to encompass memory-based decisions. The advantages of our approach over state-of-the-art POMDP solvers lie (1) in the flexibility to strengthen simple deterministic policies without losing computational tractability and (2) in the ability to enforce the provable satisfaction of arbitrarily many specifications. The latter point allows taking trade-offs between performance and safety aspects of typical POMDP examples into account. We show the effectiveness of our method on a broad range of benchmarks.

Counterexample-Guided Strategy Improvement for POMDPs Using Recurrent Neural Networks

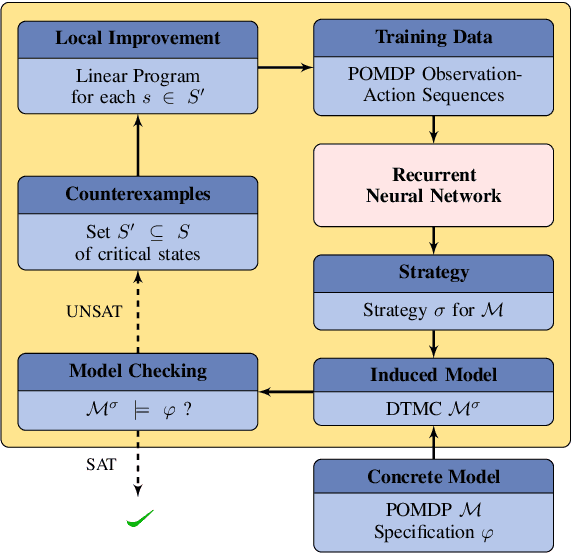
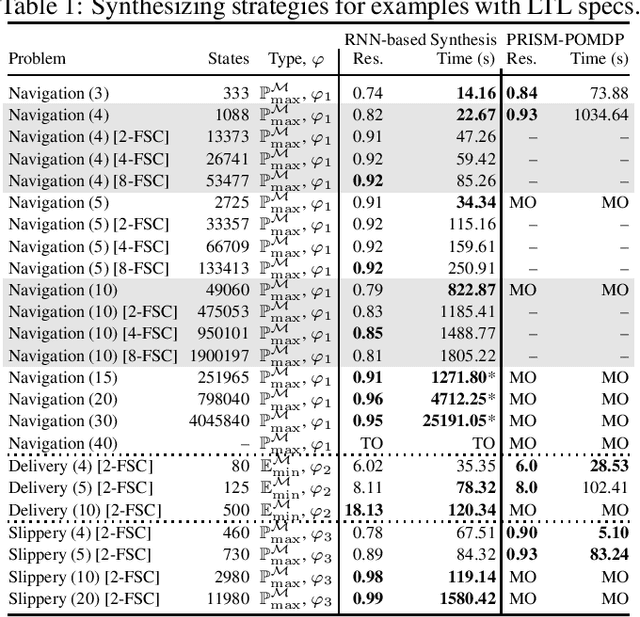
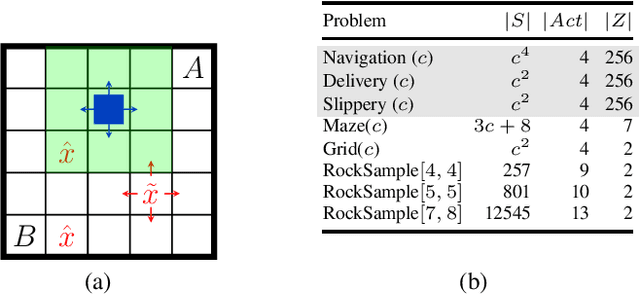
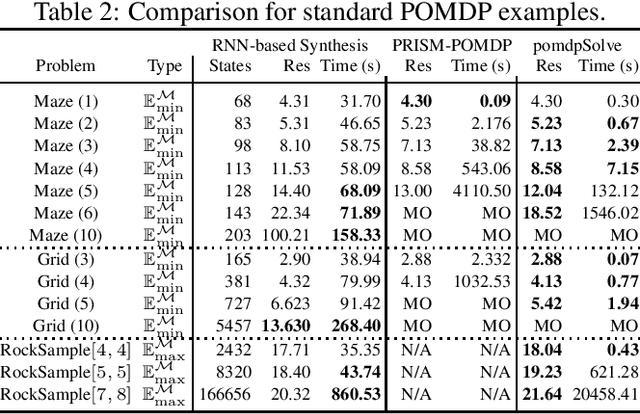
We study strategy synthesis for partially observable Markov decision processes (POMDPs). The particular problem is to determine strategies that provably adhere to (probabilistic) temporal logic constraints. This problem is computationally intractable and theoretically hard. We propose a novel method that combines techniques from machine learning and formal verification. First, we train a recurrent neural network (RNN) to encode POMDP strategies. The RNN accounts for memory-based decisions without the need to expand the full belief space of a POMDP. Secondly, we restrict the RNN-based strategy to represent a finite-memory strategy and implement it on a specific POMDP. For the resulting finite Markov chain, efficient formal verification techniques provide provable guarantees against temporal logic specifications. If the specification is not satisfied, counterexamples supply diagnostic information. We use this information to improve the strategy by iteratively training the RNN. Numerical experiments show that the proposed method elevates the state of the art in POMDP solving by up to three orders of magnitude in terms of solving times and model sizes.

Human-in-the-Loop Synthesis for Partially Observable Markov Decision Processes

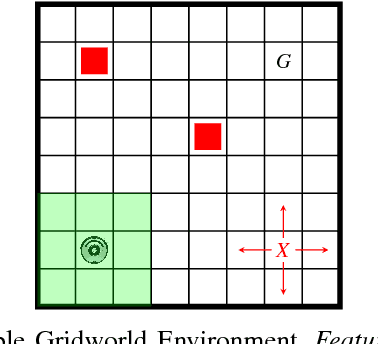
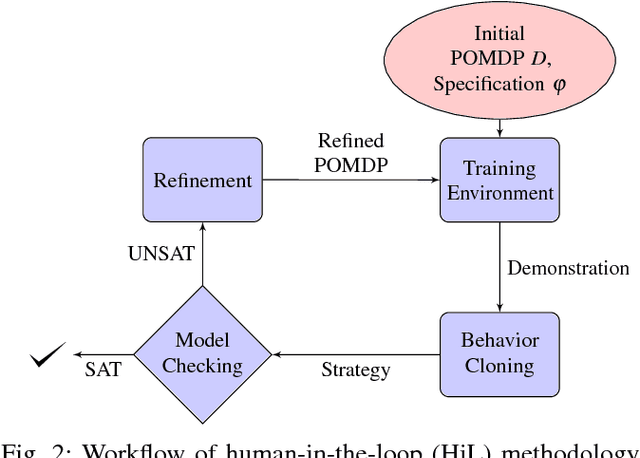
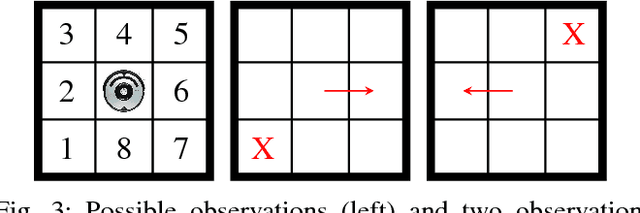
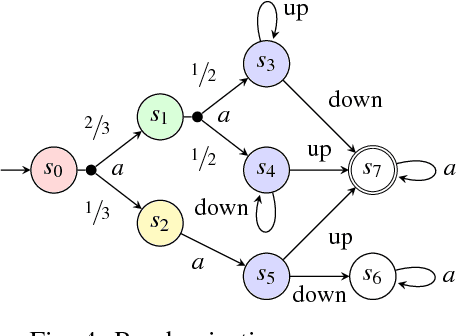
We study planning problems where autonomous agents operate inside environments that are subject to uncertainties and not fully observable. Partially observable Markov decision processes (POMDPs) are a natural formal model to capture such problems. Because of the potentially huge or even infinite belief space in POMDPs, synthesis with safety guarantees is, in general, computationally intractable. We propose an approach that aims to circumvent this difficulty: in scenarios that can be partially or fully simulated in a virtual environment, we actively integrate a human user to control an agent. While the user repeatedly tries to safely guide the agent in the simulation, we collect data from the human input. Via behavior cloning, we translate the data into a strategy for the POMDP. The strategy resolves all nondeterminism and non-observability of the POMDP, resulting in a discrete-time Markov chain (MC). The efficient verification of this MC gives quantitative insights into the quality of the inferred human strategy by proving or disproving given system specifications. For the case that the quality of the strategy is not sufficient, we propose a refinement method using counterexamples presented to the human. Experiments show that by including humans into the POMDP verification loop we improve the state of the art by orders of magnitude in terms of scalability.

Motion Planning under Partial Observability using Game-Based Abstraction

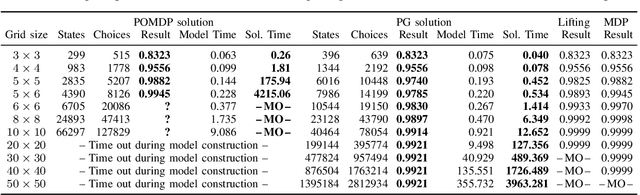
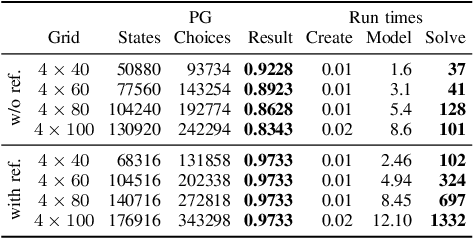
We study motion planning problems where agents move inside environments that are not fully observable and subject to uncertainties. The goal is to compute a strategy for an agent that is guaranteed to satisfy certain safety and performance specifications. Such problems are naturally modelled by partially observable Markov decision processes (POMDPs). Because of the potentially huge or even infinite belief space of POMDPs, verification and strategy synthesis is in general computationally intractable. We tackle this difficulty by exploiting typical structural properties of such scenarios; for instance, we assume that agents have the ability to observe their own positions inside an environment. Ambiguity in the state of the environment is abstracted into non-deterministic choices over the possible states of the environment. Technically, this abstraction transforms POMDPs into probabilistic two-player games (PGs). For these PGs, efficient verification tools are able to determine strategies that approximate certain measures on the POMDP. If an approximation is too coarse to provide guarantees, an abstraction refinement scheme further resolves the belief space of the POMDP. We demonstrate that our method improves the state of the art by orders of magnitude compared to a direct solution of the POMDP.