Support Consistency of Direct Sparse-Change Learning in Markov Networks

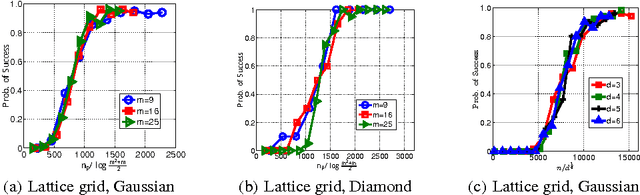
We study the problem of learning sparse structure changes between two Markov networks $P$ and $Q$. Rather than fitting two Markov networks separately to two sets of data and figuring out their differences, a recent work proposed to learn changes \emph{directly} via estimating the ratio between two Markov network models. In this paper, we give sufficient conditions for \emph{successful change detection} with respect to the sample size $n_p, n_q$, the dimension of data $m$, and the number of changed edges $d$. When using an unbounded density ratio model we prove that the true sparse changes can be consistently identified for $n_p = \Omega(d^2 \log \frac{m^2+m}{2})$ and $n_q = \Omega({n_p^2})$, with an exponentially decaying upper-bound on learning error. Such sample complexity can be improved to $\min(n_p, n_q) = \Omega(d^2 \log \frac{m^2+m}{2})$ when the boundedness of the density ratio model is assumed. Our theoretical guarantee can be applied to a wide range of discrete/continuous Markov networks.

Stochastic Dykstra Algorithms for Metric Learning on Positive Semi-Definite Cone

Recently, covariance descriptors have received much attention as powerful representations of set of points. In this research, we present a new metric learning algorithm for covariance descriptors based on the Dykstra algorithm, in which the current solution is projected onto a half-space at each iteration, and runs at O(n^3) time. We empirically demonstrate that randomizing the order of half-spaces in our Dykstra-based algorithm significantly accelerates the convergence to the optimal solution. Furthermore, we show that our approach yields promising experimental results on pattern recognition tasks.

New Descriptor for Glomerulus Detection in Kidney Microscopy Image

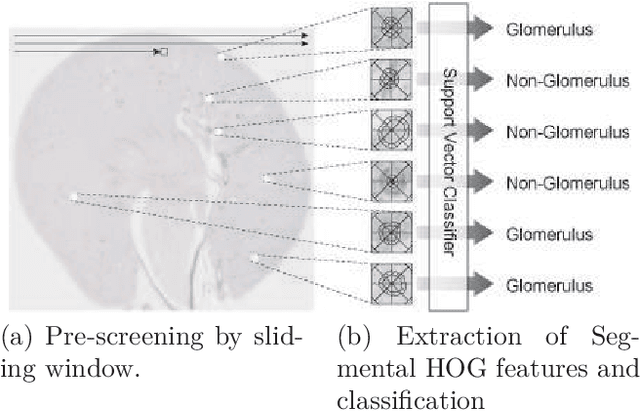
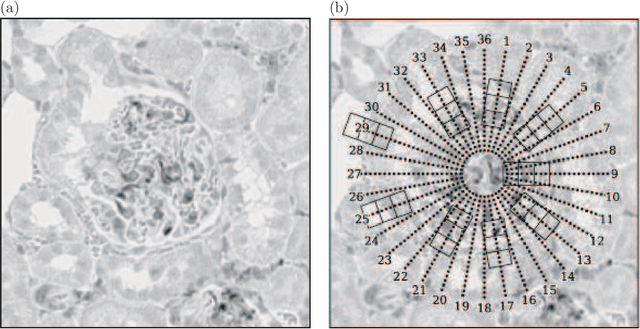
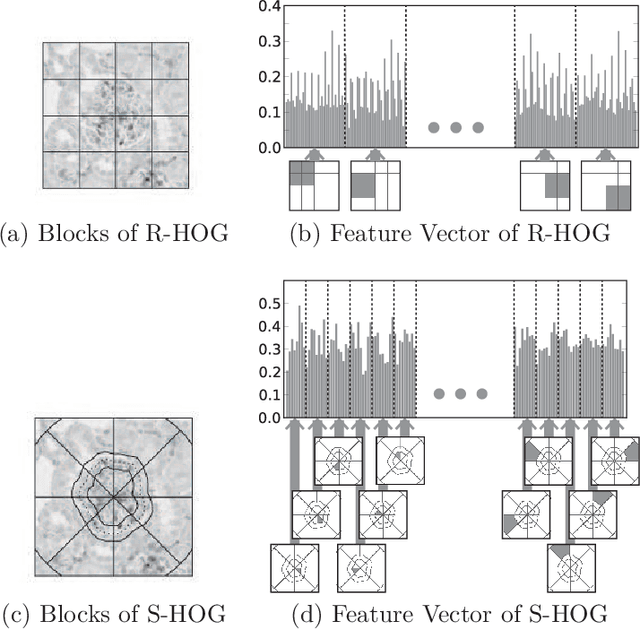
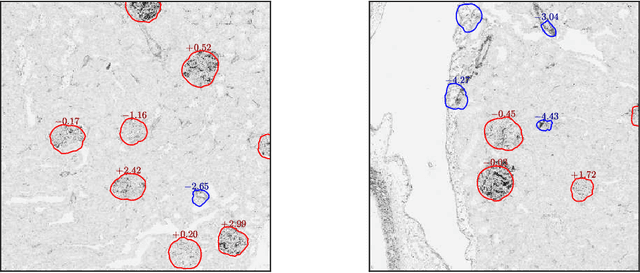
Glomerulus detection is a key step in histopathological evaluation of microscopy images of kidneys. However, the task of automatic detection of glomeruli poses challenges due to the disparity in sizes and shapes of glomeruli in renal sections. Moreover, extensive variations of their intensities due to heterogeneity in immunohistochemistry staining are also encountered. Despite being widely recognized as a powerful descriptor for general object detection, the rectangular histogram of oriented gradients (Rectangular HOG) suffers from many false positives due to the aforementioned difficulties in the context of glomerulus detection. A new descriptor referred to as Segmental HOG is developed to perform a comprehensive detection of hundreds of glomeruli in images of whole kidney sections. The new descriptor possesses flexible blocks that can be adaptively fitted to input images to acquire robustness to deformations of glomeruli. Moreover, the novel segmentation technique employed herewith generates high quality segmentation outputs and the algorithm is assured to converge to an optimal solution. Consequently, experiments using real world image data reveal that Segmental HOG achieves significant improvements in detection performance compared to Rectangular HOG. The proposed descriptor and method for glomeruli detection present promising results and is expected to be useful in pathological evaluation.