Linearly Convergent Mixup Learning

Learning in the reproducing kernel Hilbert space (RKHS) such as the support vector machine has been recognized as a promising technique. It continues to be highly effective and competitive in numerous prediction tasks, particularly in settings where there is a shortage of training data or computational limitations exist. These methods are especially valued for their ability to work with small datasets and their interpretability. To address the issue of limited training data, mixup data augmentation, widely used in deep learning, has remained challenging to apply to learning in RKHS due to the generation of intermediate class labels. Although gradient descent methods handle these labels effectively, dual optimization approaches are typically not directly applicable. In this study, we present two novel algorithms that extend to a broader range of binary classification models. Unlike gradient-based approaches, our algorithms do not require hyperparameters like learning rates, simplifying their implementation and optimization. Both the number of iterations to converge and the computational cost per iteration scale linearly with respect to the dataset size. The numerical experiments demonstrate that our algorithms achieve faster convergence to the optimal solution compared to gradient descent approaches, and that mixup data augmentation consistently improves the predictive performance across various loss functions.

A Study on Unsupervised Anomaly Detection and Defect Localization using Generative Model in Ultrasonic Non-Destructive Testing

In recent years, the deterioration of artificial materials used in structures has become a serious social issue, increasing the importance of inspections. Non-destructive testing is gaining increased demand due to its capability to inspect for defects and deterioration in structures while preserving their functionality. Among these, Laser Ultrasonic Visualization Testing (LUVT) stands out because it allows the visualization of ultrasonic propagation. This makes it visually straightforward to detect defects, thereby enhancing inspection efficiency. With the increasing number of the deterioration structures, challenges such as a shortage of inspectors and increased workload in non-destructive testing have become more apparent. Efforts to address these challenges include exploring automated inspection using machine learning. However, the lack of anomalous data with defects poses a barrier to improving the accuracy of automated inspection through machine learning. Therefore, in this study, we propose a method for automated LUVT inspection using an anomaly detection approach with a diffusion model that can be trained solely on negative examples (defect-free data). We experimentally confirmed that our proposed method improves defect detection and localization compared to general object detection algorithms used previously.

Simulation-Aided Deep Learning for Laser Ultrasonic Visualization Testing

In recent years, laser ultrasonic visualization testing (LUVT) has attracted much attention because of its ability to efficiently perform non-contact ultrasonic non-destructive testing.Despite many success reports of deep learning based image analysis for widespread areas, attempts to apply deep learning to defect detection in LUVT images face the difficulty of preparing a large dataset of LUVT images that is too expensive to scale. To compensate for the scarcity of such training data, we propose a data augmentation method that generates artificial LUVT images by simulation and applies a style transfer to simulated LUVT images.The experimental results showed that the effectiveness of data augmentation based on the style-transformed simulated images improved the prediction performance of defects, rather than directly using the raw simulated images for data augmentation.

Multi-Target Tobit Models for Completing Water Quality Data

Monitoring microbiological behaviors in water is crucial to manage public health risk from waterborne pathogens, although quantifying the concentrations of microbiological organisms in water is still challenging because concentrations of many pathogens in water samples may often be below the quantification limit, producing censoring data. To enable statistical analysis based on quantitative values, the true values of non-detected measurements are required to be estimated with high precision. Tobit model is a well-known linear regression model for analyzing censored data. One drawback of the Tobit model is that only the target variable is allowed to be censored. In this study, we devised a novel extension of the classical Tobit model, called the \emph{multi-target Tobit model}, to handle multiple censored variables simultaneously by introducing multiple target variables. For fitting the new model, a numerical stable optimization algorithm was developed based on elaborate theories. Experiments conducted using several real-world water quality datasets provided an evidence that estimating multiple columns jointly gains a great advantage over estimating them separately.

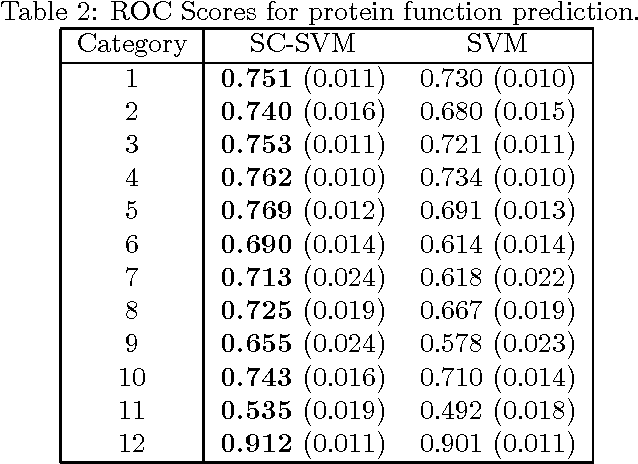
Learning Sign-Constrained Support Vector Machines

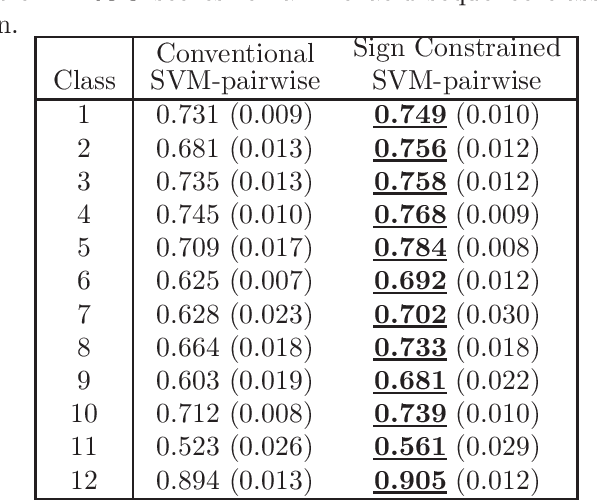
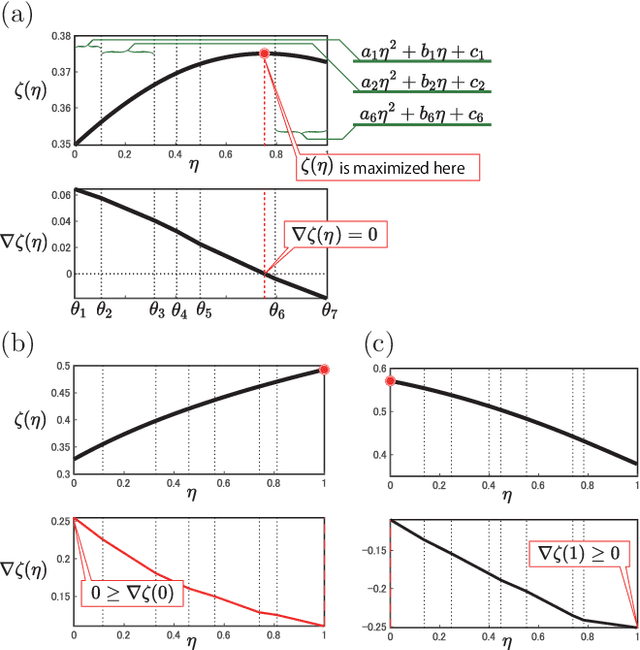
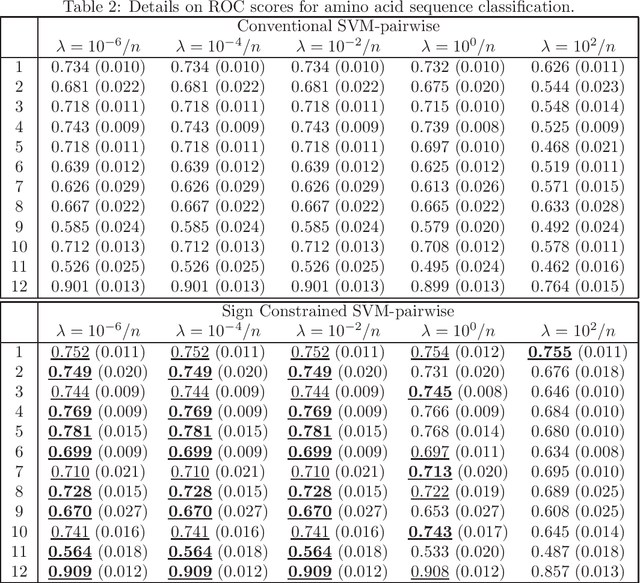
Domain knowledge is useful to improve the generalization performance of learning machines. Sign constraints are a handy representation to combine domain knowledge with learning machine. In this paper, we consider constraining the signs of the weight coefficients in learning the linear support vector machine, and develop two optimization algorithms for minimizing the empirical risk under the sign constraints. One of the two algorithms is based on the projected gradient method, in which each iteration of the projected gradient method takes $O(nd)$ computational cost and the sublinear convergence of the objective error is guaranteed. The second algorithm is based on the Frank-Wolfe method that also converges sublinearly and possesses a clear termination criterion. We show that each iteration of the Frank-Wolfe also requires $O(nd)$ cost. Furthermore, we derive the explicit expression for the minimal iteration number to ensure an $\epsilon$-accurate solution by analyzing the curvature of the objective function. Finally, we empirically demonstrate that the sign constraints are a promising technique when similarities to the training examples compose the feature vector.

Adaptive Signal Variances: CNN Initialization Through Modern Architectures

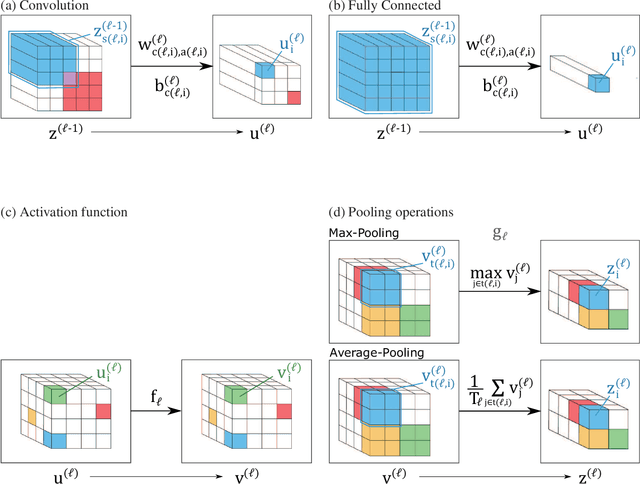
Deep convolutional neural networks (CNN) have achieved the unwavering confidence in its performance on image processing tasks. The CNN architecture constitutes a variety of different types of layers including the convolution layer and the max-pooling layer. CNN practitioners widely understand the fact that the stability of learning depends on how to initialize the model parameters in each layer. Nowadays, no one doubts that the de facto standard scheme for initialization is the so-called Kaiming initialization that has been developed by He et al. The Kaiming scheme was derived from a much simpler model than the currently used CNN structure having evolved since the emergence of the Kaiming scheme. The Kaiming model consists only of the convolution and fully connected layers, ignoring the max-pooling layer and the global average pooling layer. In this study, we derived the initialization scheme again not from the simplified Kaiming model, but precisely from the modern CNN architectures, and empirically investigated how the new initialization method performs compared to the de facto standard ones that are widely used today.

Frank-Wolfe algorithm for learning SVM-type multi-category classifiers

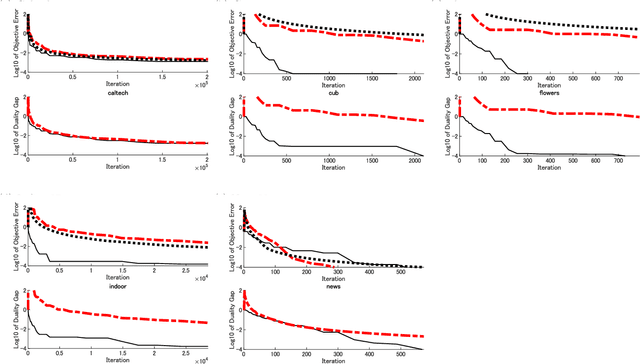
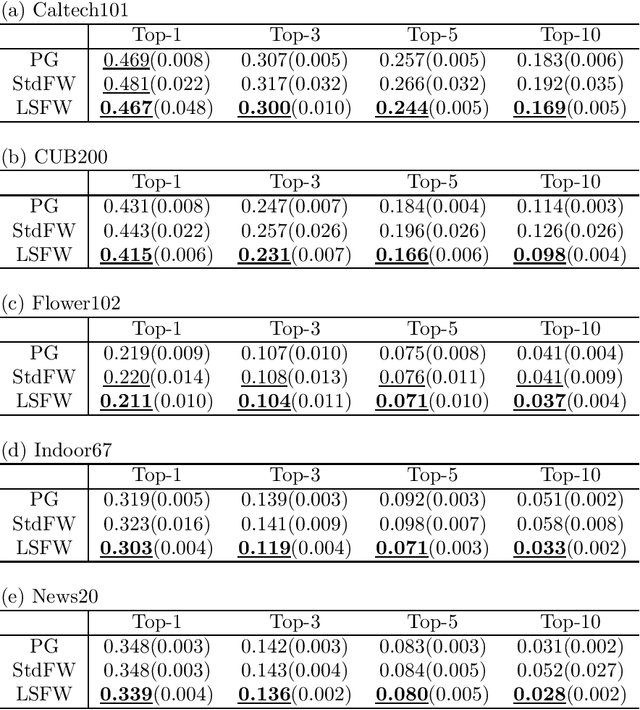
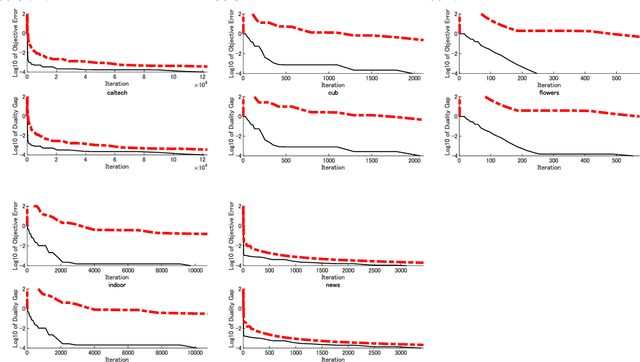
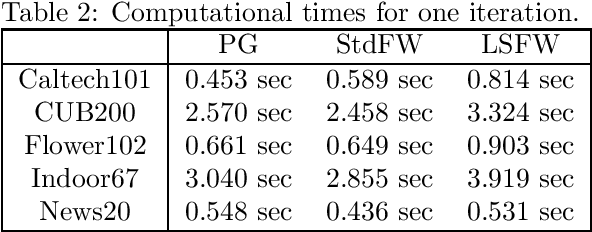
Multi-category support vector machine (MC-SVM) is one of the most popular machine learning algorithms. There are lots of variants of MC-SVM, although different optimization algorithms were developed for different learning machines. In this study, we developed a new optimization algorithm that can be applied to many of MC-SVM variants. The algorithm is based on the Frank-Wolfe framework that requires two subproblems, direction finding and line search, in each iteration. The contribution of this study is the discovery that both subproblems have a closed form solution if the Frank-Wolfe framework is applied to the dual problem. Additionally, the closed form solutions on both for the direction finding and for the line search exist even for the Moreau envelopes of the loss functions. We use several large datasets to demonstrate that the proposed optimization algorithm converges rapidly and thereby improves the pattern recognition performance.

Parametric Models for Mutual Kernel Matrix Completion

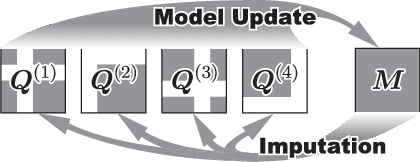
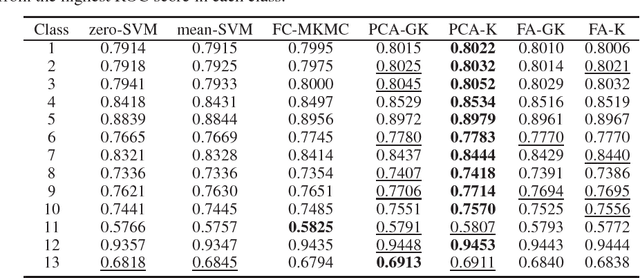
Recent studies utilize multiple kernel learning to deal with incomplete-data problem. In this study, we introduce new methods that do not only complete multiple incomplete kernel matrices simultaneously, but also allow control of the flexibility of the model by parameterizing the model matrix. By imposing restrictions on the model covariance, overfitting of the data is avoided. A limitation of kernel matrix estimations done via optimization of an objective function is that the positive definiteness of the result is not guaranteed. In view of this limitation, our proposed methods employ the LogDet divergence, which ensures the positive definiteness of the resulting inferred kernel matrix. We empirically show that our proposed restricted covariance models, employed with LogDet divergence, yield significant improvements in the generalization performance of previous completion methods.

Threshold Auto-Tuning Metric Learning

It has been reported repeatedly that discriminative learning of distance metric boosts the pattern recognition performance. A weak point of ITML-based methods is that the distance threshold for similarity/dissimilarity constraints must be determined manually and it is sensitive to generalization performance, although the ITML-based methods enjoy an advantage that the Bregman projection framework can be applied for optimization of distance metric. In this paper, we present a new formulation of metric learning algorithm in which the distance threshold is optimized together. Since the optimization is still in the Bregman projection framework, the Dykstra algorithm can be applied for optimization. A nonlinear equation has to be solved to project the solution onto a half-space in each iteration. Na\"{i}ve method takes $O(LMn^{3})$ computational time to solve the nonlinear equation. In this study, an efficient technique that can solve the nonlinear equation in $O(Mn^{3})$ has been discovered. We have proved that the root exists and is unique. We empirically show that the accuracy of pattern recognition for the proposed metric learning algorithm is comparable to the existing metric learning methods, yet the distance threshold is automatically tuned for the proposed metric learning algorithm.

Sign-Constrained Regularized Loss Minimization

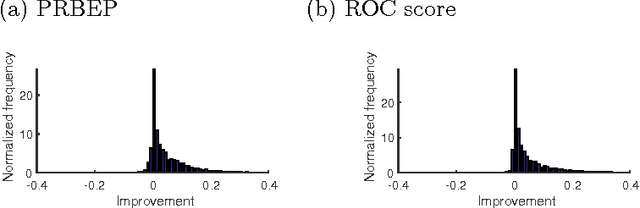
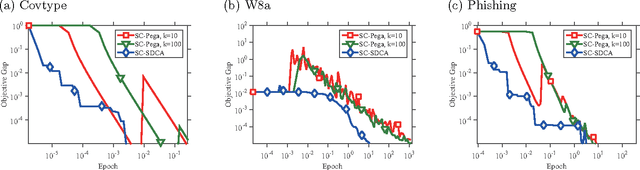
In practical analysis, domain knowledge about analysis target has often been accumulated, although, typically, such knowledge has been discarded in the statistical analysis stage, and the statistical tool has been applied as a black box. In this paper, we introduce sign constraints that are a handy and simple representation for non-experts in generic learning problems. We have developed two new optimization algorithms for the sign-constrained regularized loss minimization, called the sign-constrained Pegasos (SC-Pega) and the sign-constrained SDCA (SC-SDCA), by simply inserting the sign correction step into the original Pegasos and SDCA, respectively. We present theoretical analyses that guarantee that insertion of the sign correction step does not degrade the convergence rate for both algorithms. Two applications, where the sign-constrained learning is effective, are presented. The one is exploitation of prior information about correlation between explanatory variables and a target variable. The other is introduction of the sign-constrained to SVM-Pairwise method. Experimental results demonstrate significant improvement of generalization performance by introducing sign constraints in both applications.