Support Consistency of Direct Sparse-Change Learning in Markov Networks

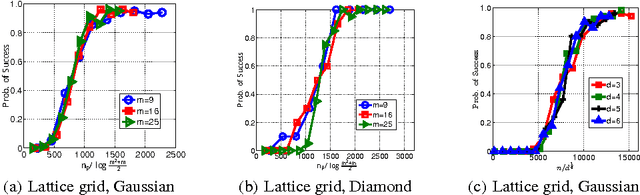
We study the problem of learning sparse structure changes between two Markov networks $P$ and $Q$. Rather than fitting two Markov networks separately to two sets of data and figuring out their differences, a recent work proposed to learn changes \emph{directly} via estimating the ratio between two Markov network models. In this paper, we give sufficient conditions for \emph{successful change detection} with respect to the sample size $n_p, n_q$, the dimension of data $m$, and the number of changed edges $d$. When using an unbounded density ratio model we prove that the true sparse changes can be consistently identified for $n_p = \Omega(d^2 \log \frac{m^2+m}{2})$ and $n_q = \Omega({n_p^2})$, with an exponentially decaying upper-bound on learning error. Such sample complexity can be improved to $\min(n_p, n_q) = \Omega(d^2 \log \frac{m^2+m}{2})$ when the boundedness of the density ratio model is assumed. Our theoretical guarantee can be applied to a wide range of discrete/continuous Markov networks.

Stochastic Dykstra Algorithms for Metric Learning on Positive Semi-Definite Cone

Recently, covariance descriptors have received much attention as powerful representations of set of points. In this research, we present a new metric learning algorithm for covariance descriptors based on the Dykstra algorithm, in which the current solution is projected onto a half-space at each iteration, and runs at O(n^3) time. We empirically demonstrate that randomizing the order of half-spaces in our Dykstra-based algorithm significantly accelerates the convergence to the optimal solution. Furthermore, we show that our approach yields promising experimental results on pattern recognition tasks.

Least-Squares Independence Regression for Non-Linear Causal Inference under Non-Gaussian Noise

The discovery of non-linear causal relationship under additive non-Gaussian noise models has attracted considerable attention recently because of their high flexibility. In this paper, we propose a novel causal inference algorithm called least-squares independence regression (LSIR). LSIR learns the additive noise model through the minimization of an estimator of the squared-loss mutual information between inputs and residuals. A notable advantage of LSIR over existing approaches is that tuning parameters such as the kernel width and the regularization parameter can be naturally optimized by cross-validation, allowing us to avoid overfitting in a data-dependent fashion. Through experiments with real-world datasets, we show that LSIR compares favorably with a state-of-the-art causal inference method.