PICore: Physics-Informed Unsupervised Coreset Selection for Data Efficient Neural Operator Training

Neural operators offer a powerful paradigm for solving partial differential equations (PDEs) that cannot be solved analytically by learning mappings between function spaces. However, there are two main bottlenecks in training neural operators: they require a significant amount of training data to learn these mappings, and this data needs to be labeled, which can only be accessed via expensive simulations with numerical solvers. To alleviate both of these issues simultaneously, we propose PICore, an unsupervised coreset selection framework that identifies the most informative training samples without requiring access to ground-truth PDE solutions. PICore leverages a physics-informed loss to select unlabeled inputs by their potential contribution to operator learning. After selecting a compact subset of inputs, only those samples are simulated using numerical solvers to generate labels, reducing annotation costs. We then train the neural operator on the reduced labeled dataset, significantly decreasing training time as well. Across four diverse PDE benchmarks and multiple coreset selection strategies, PICore achieves up to 78% average increase in training efficiency relative to supervised coreset selection methods with minimal changes in accuracy. We provide code at https://github.com/Asatheesh6561/PICore.

Stability of sorting based embeddings

Consider a group $G$ of order $M$ acting unitarily on a real inner product space $V$. We show that the sorting based embedding obtained by applying a general linear map $\alpha : \mathbb{R}^{M \times N} \to \mathbb{R}^D$ to the invariant map $\beta_\Phi : V \to \mathbb{R}^{M \times N}$ given by sorting the coorbits $(\langle v, g \phi_i \rangle_V)_{g \in G}$, where $(\phi_i)_{i=1}^N \in V$, satisfies a bi-Lipschitz condition if and only if it separates orbits. Additionally, we note that any invariant Lipschitz continuous map (into a Hilbert space) factors through the sorting based embedding, and that any invariant continuous map (into a locally convex space) factors through the sorting based embedding as well.

Approximation of the Proximal Operator of the $\ell_\infty$ Norm Using a Neural Network

Computing the proximal operator of the $\ell_\infty$ norm, $\textbf{prox}_{\alpha ||\cdot||_\infty}(\mathbf{x})$, generally requires a sort of the input data, or at least a partial sort similar to quicksort. In order to avoid using a sort, we present an $O(m)$ approximation of $\textbf{prox}_{\alpha ||\cdot||_\infty}(\mathbf{x})$ using a neural network. A novel aspect of the network is that it is able to accept vectors of varying lengths due to a feature selection process that uses moments of the input data. We present results on the accuracy of the approximation, feature importance, and computational efficiency of the approach. We show that the network outperforms a "vanilla neural network" that does not use feature selection. We also present an algorithm with corresponding theory to calculate $\textbf{prox}_{\alpha ||\cdot||_\infty}(\mathbf{x})$ exactly, relate it to the Moreau decomposition, and compare its computational efficiency to that of the approximation.

Coupled Multiwavelet Neural Operator Learning for Coupled Partial Differential Equations

Coupled partial differential equations (PDEs) are key tasks in modeling the complex dynamics of many physical processes. Recently, neural operators have shown the ability to solve PDEs by learning the integral kernel directly in Fourier/Wavelet space, so the difficulty for solving the coupled PDEs depends on dealing with the coupled mappings between the functions. Towards this end, we propose a \textit{coupled multiwavelets neural operator} (CMWNO) learning scheme by decoupling the coupled integral kernels during the multiwavelet decomposition and reconstruction procedures in the Wavelet space. The proposed model achieves significantly higher accuracy compared to previous learning-based solvers in solving the coupled PDEs including Gray-Scott (GS) equations and the non-local mean field game (MFG) problem. According to our experimental results, the proposed model exhibits a $2\times \sim 4\times$ improvement relative $L$2 error compared to the best results from the state-of-the-art models.

VQ-Flows: Vector Quantized Local Normalizing Flows

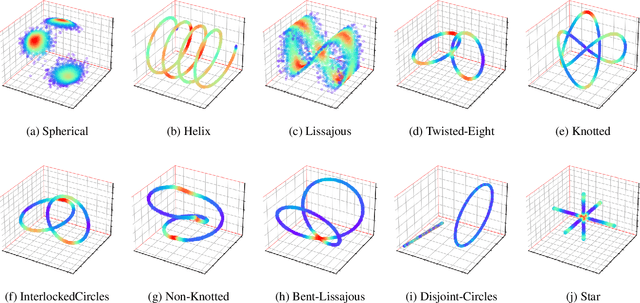
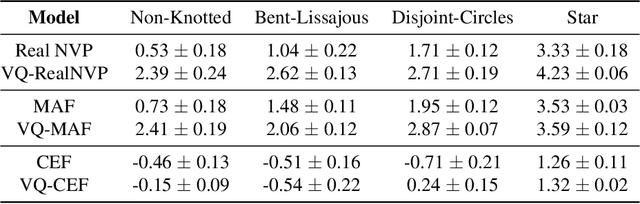
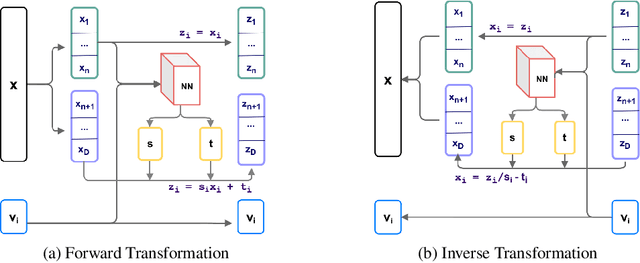
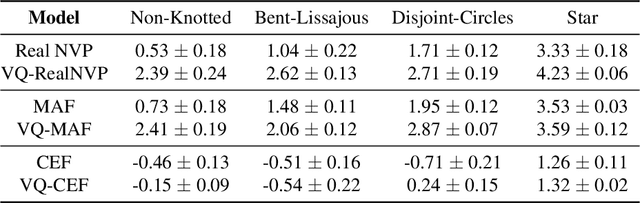
Normalizing flows provide an elegant approach to generative modeling that allows for efficient sampling and exact density evaluation of unknown data distributions. However, current techniques have significant limitations in their expressivity when the data distribution is supported on a low-dimensional manifold or has a non-trivial topology. We introduce a novel statistical framework for learning a mixture of local normalizing flows as "chart maps" over the data manifold. Our framework augments the expressivity of recent approaches while preserving the signature property of normalizing flows, that they admit exact density evaluation. We learn a suitable atlas of charts for the data manifold via a vector quantized auto-encoder (VQ-AE) and the distributions over them using a conditional flow. We validate experimentally that our probabilistic framework enables existing approaches to better model data distributions over complex manifolds.

Permutation Invariant Representations with Applications to Graph Deep Learning

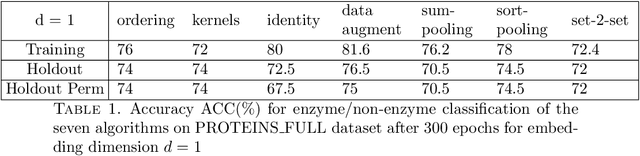
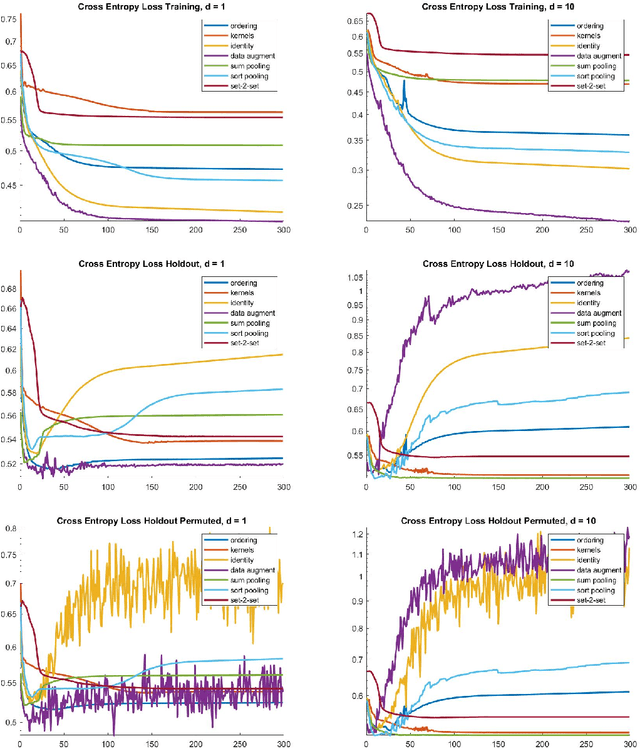
This paper presents primarily two Euclidean embeddings of the quotient space generated by matrices that are identified modulo arbitrary row permutations. The original application is in deep learning on graphs where the learning task is invariant to node relabeling. Two embedding schemes are introduced, one based on sorting and the other based on algebras of multivariate polynomials. While both embeddings exhibit a computational complexity exponential in problem size, the sorting based embedding is globally bi-Lipschitz and admits a low dimensional target space. Additionally, an almost everywhere injective scheme can be implemented with minimal redundancy and low computational cost. In turn, this proves that almost any classifier can be implemented with an arbitrary small loss of performance. Numerical experiments are carried out on two data sets, a chemical compound data set (QM9) and a proteins data set (PROTEINS).

Convergence Guarantees for Deep Epsilon Greedy Policy Learning

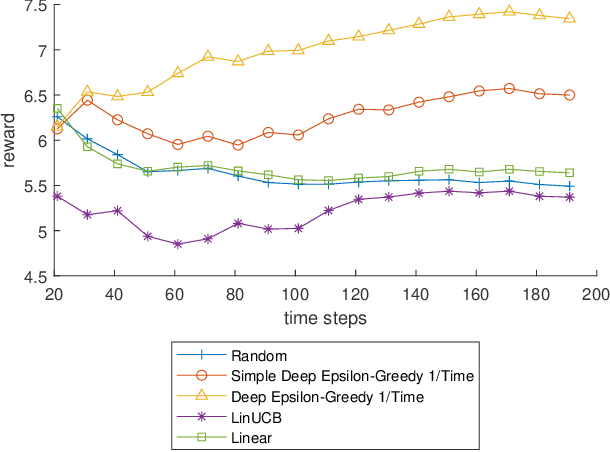
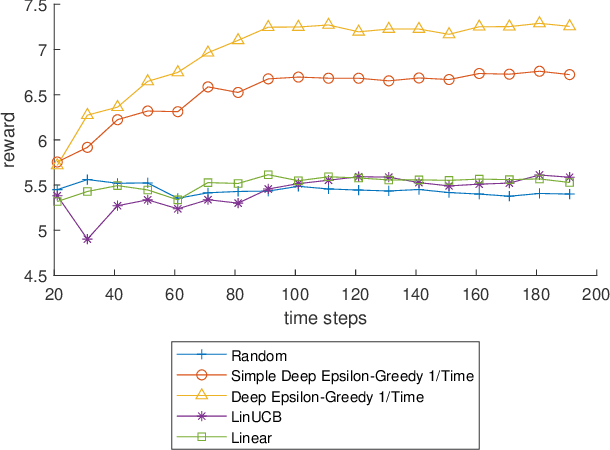
Policy learning is a quickly growing area. As robotics and computers control day-to-day life, their error rate needs to be minimized and controlled. There are many policy learning methods and provable error rates that accompany them. We show an error or regret bound and convergence of the Deep Epsilon Greedy method which chooses actions with a neural network's prediction. In experiments with the real-world dataset MNIST, we construct a nonlinear reinforcement learning problem. We witness how with either high or low noise, some methods do and some do not converge which agrees with our proof of convergence.

An Exact Hypergraph Matching Algorithm for Nuclear Identification in Embryonic Caenorhabditis elegans

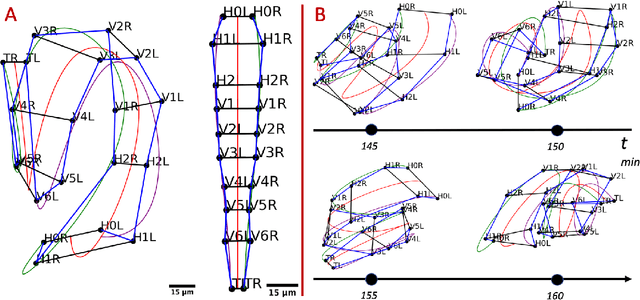
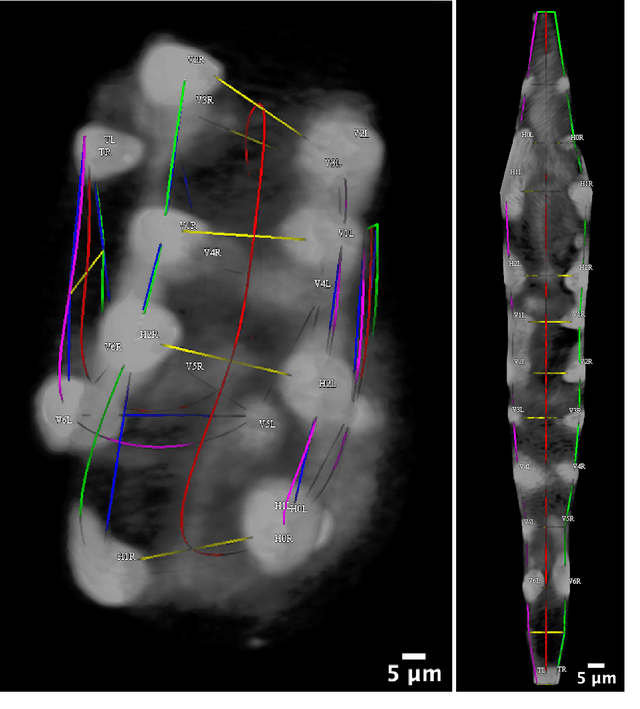
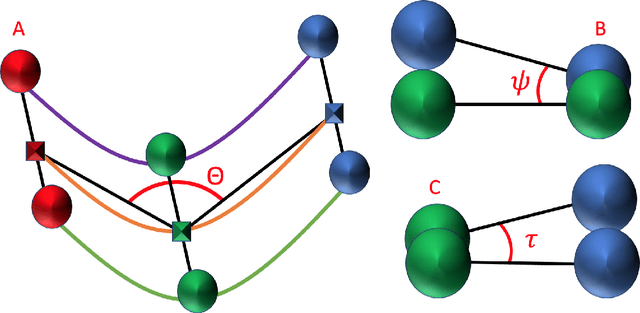
Finding an optimal correspondence between point sets is a common task in computer vision. Existing techniques assume relatively simple relationships among points and do not guarantee an optimal match. We introduce an algorithm capable of exactly solving point set matching by modeling the task as hypergraph matching. The algorithm extends the classical branch and bound paradigm to select and aggregate vertices under a proposed decomposition of the multilinear objective function. The methodology is motivated by Caenorhabditis elegans, a model organism used frequently in developmental biology and neurobiology. The embryonic C. elegans contains seam cells that can act as fiducial markers allowing the identification of other nuclei during embryo development. The proposed algorithm identifies seam cells more accurately than established point-set matching methods, while providing a framework to approach other similarly complex point set matching tasks.

On Lipschitz Bounds of General Convolutional Neural Networks

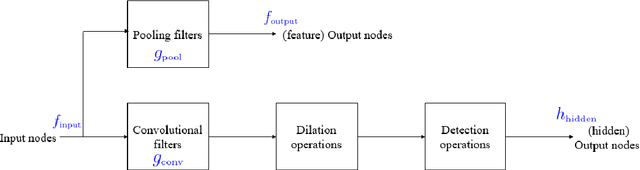
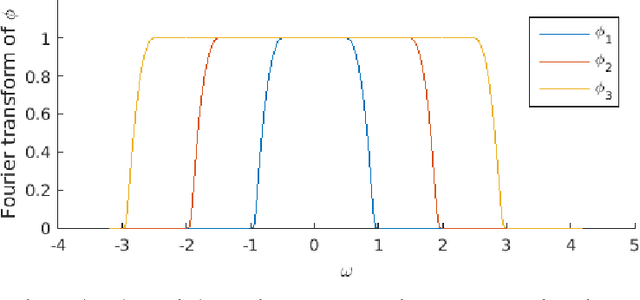
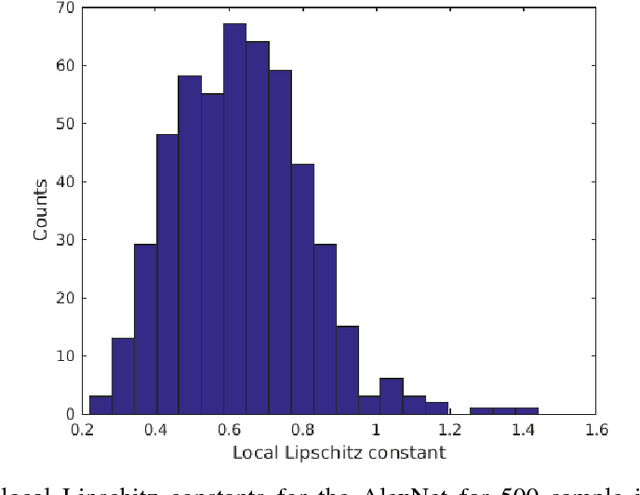
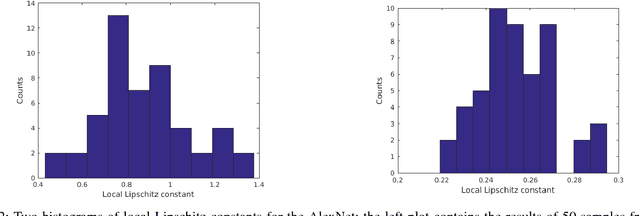
Many convolutional neural networks (CNNs) have a feed-forward structure. In this paper, a linear program that estimates the Lipschitz bound of such CNNs is proposed. Several CNNs, including the scattering networks, the AlexNet and the GoogleNet, are studied numerically and compared to the theoretical bounds. Next, concentration inequalities of the output distribution to a stationary random input signal expressed in terms of the Lipschitz bound are established. The Lipschitz bound is further used to establish a nonlinear discriminant analysis designed to measure the separation between features of different classes.

Learning flexible representations of stochastic processes on graphs

Graph convolutional networks adapt the architecture of convolutional neural networks to learn rich representations of data supported on arbitrary graphs by replacing the convolution operations of convolutional neural networks with graph-dependent linear operations. However, these graph-dependent linear operations are developed for scalar functions supported on undirected graphs. We propose a class of linear operations for stochastic (time-varying) processes on directed (or undirected) graphs to be used in graph convolutional networks. We propose a parameterization of such linear operations using functional calculus to achieve arbitrarily low learning complexity. The proposed approach is shown to model richer behaviors and display greater flexibility in learning representations than product graph methods.