Quentin Berthet
Efficient and Modular Implicit Differentiation
May 31, 2021

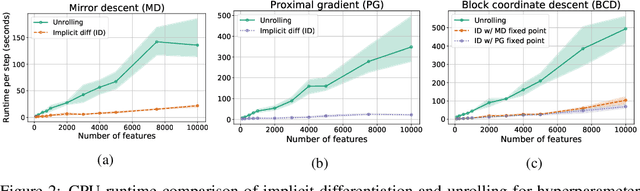

Abstract:Automatic differentiation (autodiff) has revolutionized machine learning. It allows expressing complex computations by composing elementary ones in creative ways and removes the burden of computing their derivatives by hand. More recently, differentiation of optimization problem solutions has attracted widespread attention with applications such as optimization as a layer, and in bi-level problems such as hyper-parameter optimization and meta-learning. However, the formulas for these derivatives often involve case-by-case tedious mathematical derivations. In this paper, we propose a unified, efficient and modular approach for implicit differentiation of optimization problems. In our approach, the user defines (in Python in the case of our implementation) a function $F$ capturing the optimality conditions of the problem to be differentiated. Once this is done, we leverage autodiff of $F$ and implicit differentiation to automatically differentiate the optimization problem. Our approach thus combines the benefits of implicit differentiation and autodiff. It is efficient as it can be added on top of any state-of-the-art solver and modular as the optimality condition specification is decoupled from the implicit differentiation mechanism. We show that seemingly simple principles allow to recover many recently proposed implicit differentiation methods and create new ones easily. We demonstrate the ease of formulating and solving bi-level optimization problems using our framework. We also showcase an application to the sensitivity analysis of molecular dynamics.
Self-Supervised Learning of Audio Representations from Permutations with Differentiable Ranking
Mar 17, 2021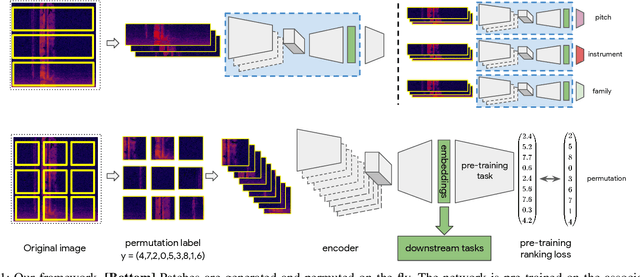
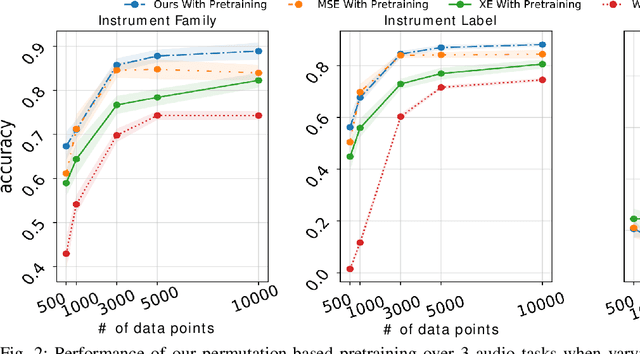
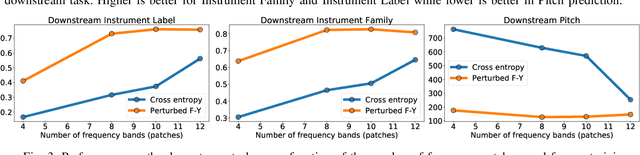
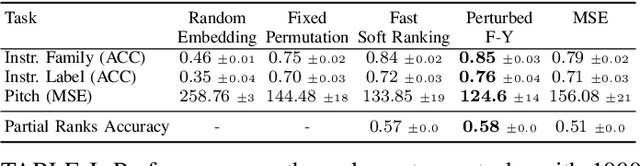
Abstract:Self-supervised pre-training using so-called "pretext" tasks has recently shown impressive performance across a wide range of modalities. In this work, we advance self-supervised learning from permutations, by pre-training a model to reorder shuffled parts of the spectrogram of an audio signal, to improve downstream classification performance. We make two main contributions. First, we overcome the main challenges of integrating permutation inversions into an end-to-end training scheme, using recent advances in differentiable ranking. This was heretofore sidestepped by casting the reordering task as classification, fundamentally reducing the space of permutations that can be exploited. Our experiments validate that learning from all possible permutations improves the quality of the pre-trained representations over using a limited, fixed set. Second, we show that inverting permutations is a meaningful pretext task for learning audio representations in an unsupervised fashion. In particular, we improve instrument classification and pitch estimation of musical notes by reordering spectrogram patches in the time-frequency space.
Fast Differentiable Sorting and Ranking
Feb 20, 2020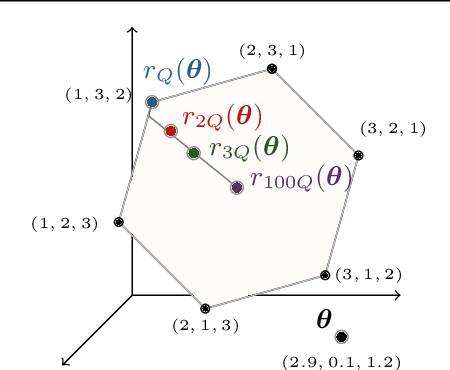
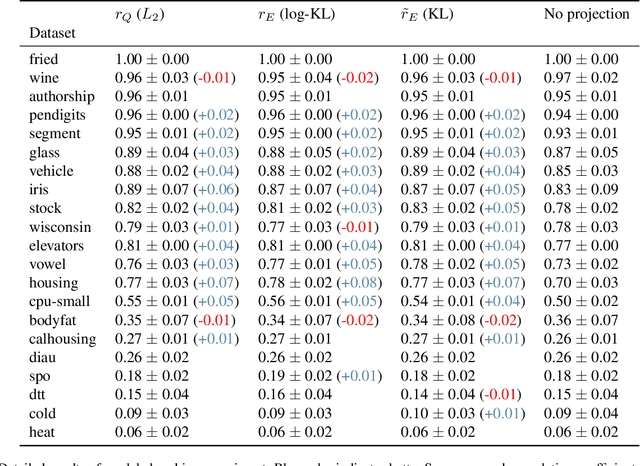
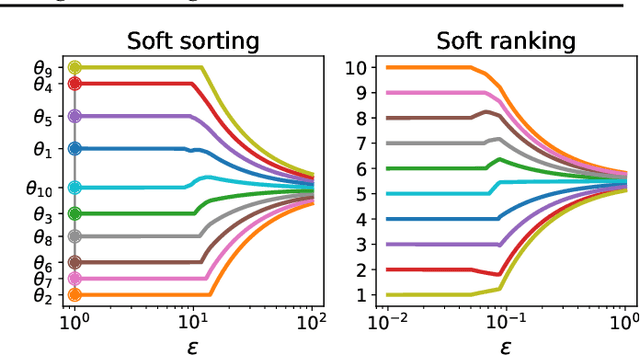
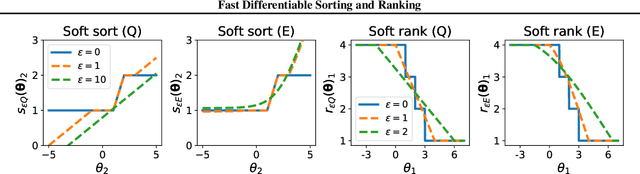
Abstract:The sorting operation is one of the most basic and commonly used building blocks in computer programming. In machine learning, it is commonly used for robust statistics. However, seen as a function, it is piecewise linear and as a result includes many kinks at which it is non-differentiable. More problematic is the related ranking operator, commonly used for order statistics and ranking metrics. It is a piecewise constant function, meaning that its derivatives are null or undefined. While numerous works have proposed differentiable proxies to sorting and ranking, they do not achieve the $O(n \log n)$ time complexity one would expect from sorting and ranking operations. In this paper, we propose the first differentiable sorting and ranking operators with $O(n \log n)$ time and $O(n)$ space complexity. Our proposal in addition enjoys exact computation and differentiation. We achieve this feat by constructing differentiable sorting and ranking operators as projections onto the permutahedron, the convex hull of permutations, and using a reduction to isotonic optimization. Empirically, we confirm that our approach is an order of magnitude faster than existing approaches and showcase two novel applications: differentiable Spearman's rank correlation coefficient and soft least trimmed squares.
Stochastic Optimization for Regularized Wasserstein Estimators
Feb 20, 2020


Abstract:Optimal transport is a foundational problem in optimization, that allows to compare probability distributions while taking into account geometric aspects. Its optimal objective value, the Wasserstein distance, provides an important loss between distributions that has been used in many applications throughout machine learning and statistics. Recent algorithmic progress on this problem and its regularized versions have made these tools increasingly popular. However, existing techniques require solving an optimization problem to obtain a single gradient of the loss, thus slowing down first-order methods to minimize the sum of losses, that require many such gradient computations. In this work, we introduce an algorithm to solve a regularized version of this problem of Wasserstein estimators, with a time per step which is sublinear in the natural dimensions of the problem. We introduce a dual formulation, and optimize it with stochastic gradient steps that can be computed directly from samples, without solving additional optimization problems at each step. Doing so, the estimation and computation tasks are performed jointly. We show that this algorithm can be extended to other tasks, including estimation of Wasserstein barycenters. We provide theoretical guarantees and illustrate the performance of our algorithm with experiments on synthetic data.
Learning with Differentiable Perturbed Optimizers
Feb 20, 2020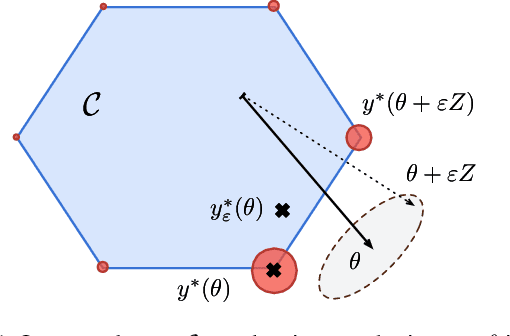
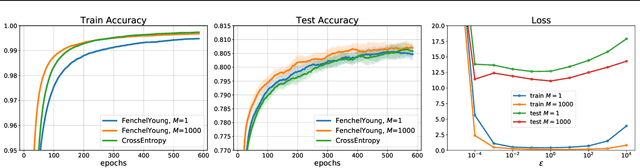

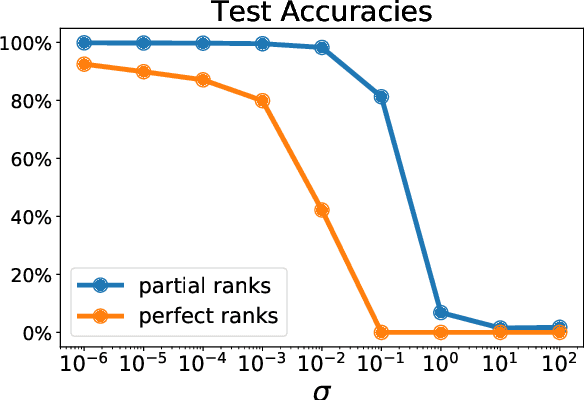
Abstract:Machine learning pipelines often rely on optimization procedures to make discrete decisions (e.g. sorting, picking closest neighbors, finding shortest paths or optimal matchings). Although these discrete decisions are easily computed in a forward manner, they cannot be used to modify model parameters using first-order optimization techniques because they break the back-propagation of computational graphs. In order to expand the scope of learning problems that can be solved in an end-to-end fashion, we propose a systematic method to transform a block that outputs an optimal discrete decision into a differentiable operation. Our approach relies on stochastic perturbations of these parameters, and can be used readily within existing solvers without the need for ad hoc regularization or smoothing. These perturbed optimizers yield solutions that are differentiable and never locally constant. The amount of smoothness can be tuned via the chosen noise amplitude, whose impact we analyze. The derivatives of these perturbed solvers can be evaluated efficiently. We also show how this framework can be connected to a family of losses developed in structured prediction, and describe how these can be used in unsupervised and supervised learning, with theoretical guarantees. We demonstrate the performance of our approach on several machine learning tasks in experiments on synthetic and real data.
Regularized Contextual Bandits
Oct 11, 2018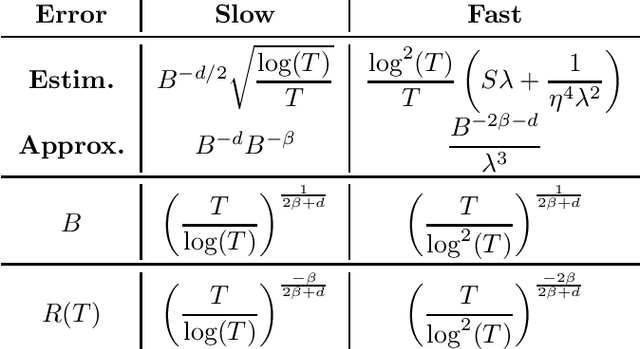
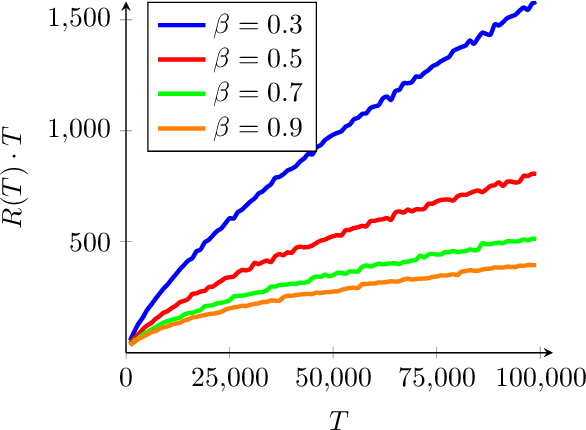
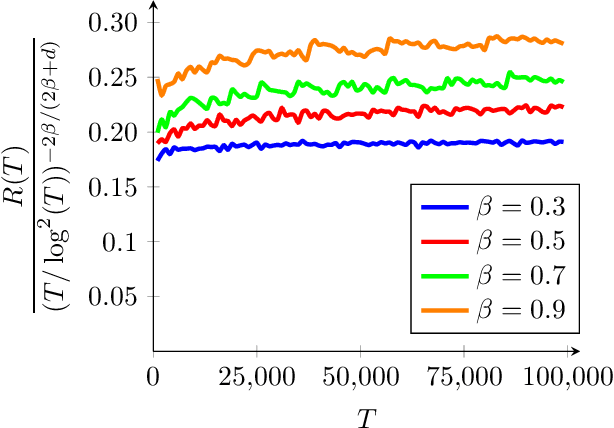
Abstract:We consider the stochastic contextual bandit problem with additional regularization. The motivation comes from problems where the policy of the agent must be close to some baseline policy which is known to perform well on the task. To tackle this problem we use a nonparametric model and propose an algorithm splitting the context space into bins, and solving simultaneously - and independently - regularized multi-armed bandit instances on each bin. We derive slow and fast rates of convergence, depending on the unknown complexity of the problem. We also consider a new relevant margin condition to get problem-independent convergence rates, ending up in intermediate convergence rates interpolating between the aforementioned slow and fast rates.
Statistical Windows in Testing for the Initial Distribution of a Reversible Markov Chain
Aug 06, 2018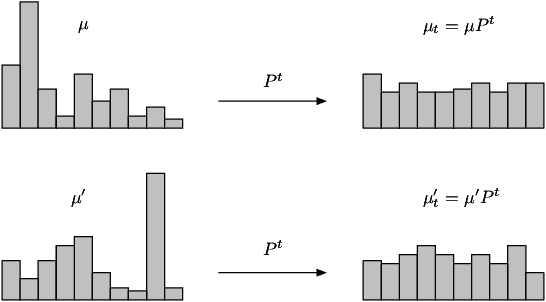

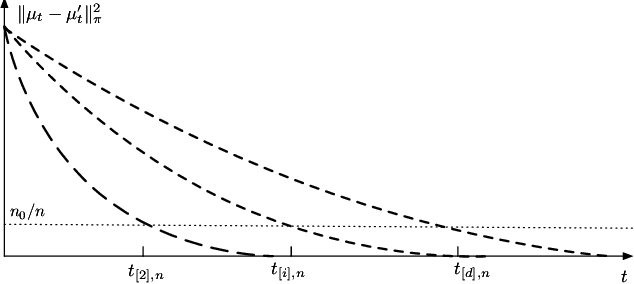
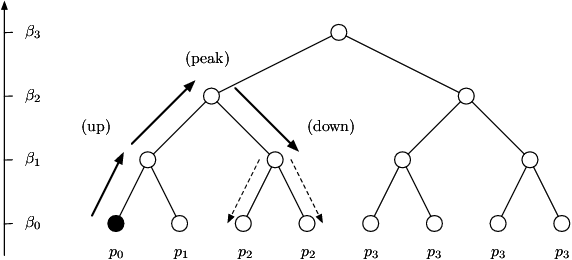
Abstract:We study the problem of hypothesis testing between two discrete distributions, where we only have access to samples after the action of a known reversible Markov chain, playing the role of noise. We derive instance-dependent minimax rates for the sample complexity of this problem, and show how its dependence in time is related to the spectral properties of the Markov chain. We show that there exists a wide statistical window, in terms of sample complexity for hypothesis testing between different pairs of initial distributions. We illustrate these results in several concrete examples.
Unsupervised Alignment of Embeddings with Wasserstein Procrustes
May 29, 2018

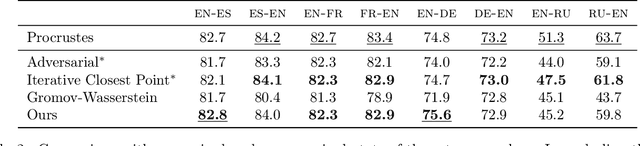

Abstract:We consider the task of aligning two sets of points in high dimension, which has many applications in natural language processing and computer vision. As an example, it was recently shown that it is possible to infer a bilingual lexicon, without supervised data, by aligning word embeddings trained on monolingual data. These recent advances are based on adversarial training to learn the mapping between the two embeddings. In this paper, we propose to use an alternative formulation, based on the joint estimation of an orthogonal matrix and a permutation matrix. While this problem is not convex, we propose to initialize our optimization algorithm by using a convex relaxation, traditionally considered for the graph isomorphism problem. We propose a stochastic algorithm to minimize our cost function on large scale problems. Finally, we evaluate our method on the problem of unsupervised word translation, by aligning word embeddings trained on monolingual data. On this task, our method obtains state of the art results, while requiring less computational resources than competing approaches.
Optimal link prediction with matrix logistic regression
Mar 19, 2018

Abstract:We consider the problem of link prediction, based on partial observation of a large network, and on side information associated to its vertices. The generative model is formulated as a matrix logistic regression. The performance of the model is analysed in a high-dimensional regime under a structural assumption. The minimax rate for the Frobenius-norm risk is established and a combinatorial estimator based on the penalised maximum likelihood approach is shown to achieve it. Furthermore, it is shown that this rate cannot be attained by any (randomised) algorithm computable in polynomial time under a computational complexity assumption.
Fast Rates for Bandit Optimization with Upper-Confidence Frank-Wolfe
Sep 06, 2017Abstract:We consider the problem of bandit optimization, inspired by stochastic optimization and online learning problems with bandit feedback. In this problem, the objective is to minimize a global loss function of all the actions, not necessarily a cumulative loss. This framework allows us to study a very general class of problems, with applications in statistics, machine learning, and other fields. To solve this problem, we analyze the Upper-Confidence Frank-Wolfe algorithm, inspired by techniques for bandits and convex optimization. We give theoretical guarantees for the performance of this algorithm over various classes of functions, and discuss the optimality of these results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge