MicroEvoEval: A Systematic Evaluation Framework for Image-Based Microstructure Evolution Prediction

Simulating microstructure evolution (MicroEvo) is vital for materials design but demands high numerical accuracy, efficiency, and physical fidelity. Although recent studies on deep learning (DL) offer a promising alternative to traditional solvers, the field lacks standardized benchmarks. Existing studies are flawed due to a lack of comparing specialized MicroEvo DL models with state-of-the-art spatio-temporal architectures, an overemphasis on numerical accuracy over physical fidelity, and a failure to analyze error propagation over time. To address these gaps, we introduce MicroEvoEval, the first comprehensive benchmark for image-based microstructure evolution prediction. We evaluate 14 models, encompassing both domain-specific and general-purpose architectures, across four representative MicroEvo tasks with datasets specifically structured for both short- and long-term assessment. Our multi-faceted evaluation framework goes beyond numerical accuracy and computational cost, incorporating a curated set of structure-preserving metrics to assess physical fidelity. Our extensive evaluations yield several key insights. Notably, we find that modern architectures (e.g., VMamba), not only achieve superior long-term stability and physical fidelity but also operate with an order-of-magnitude greater computational efficiency. The results highlight the necessity of holistic evaluation and identify these modern architectures as a highly promising direction for developing efficient and reliable surrogate models in data-driven materials science.

Large-Scale Kernel Methods for Independence Testing

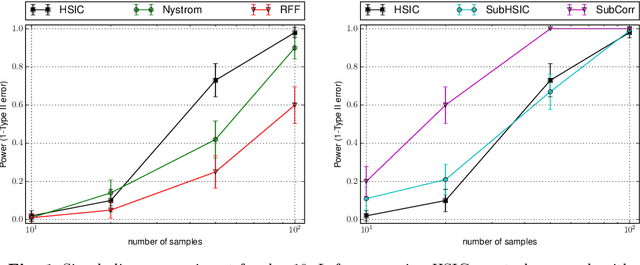
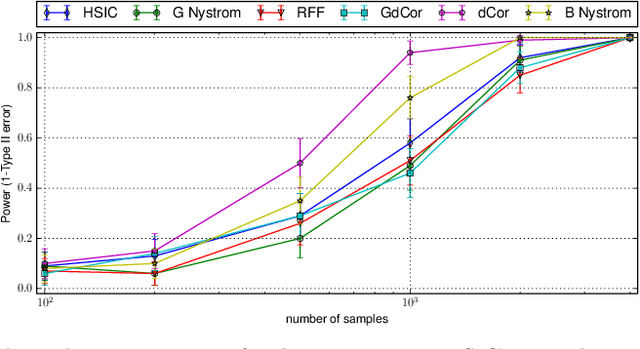
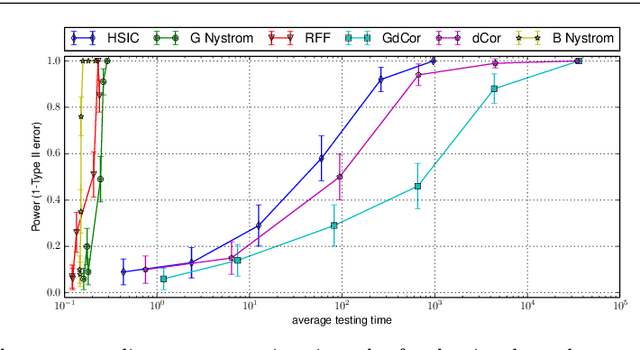
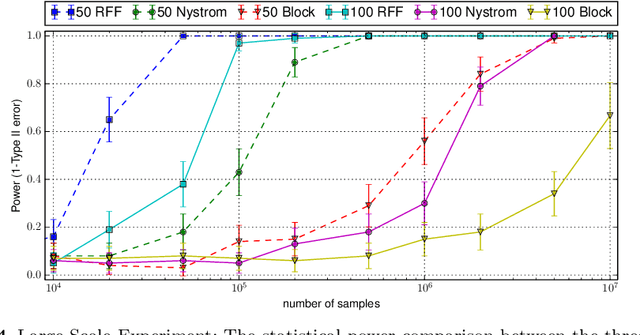
Representations of probability measures in reproducing kernel Hilbert spaces provide a flexible framework for fully nonparametric hypothesis tests of independence, which can capture any type of departure from independence, including nonlinear associations and multivariate interactions. However, these approaches come with an at least quadratic computational cost in the number of observations, which can be prohibitive in many applications. Arguably, it is exactly in such large-scale datasets that capturing any type of dependence is of interest, so striking a favourable tradeoff between computational efficiency and test performance for kernel independence tests would have a direct impact on their applicability in practice. In this contribution, we provide an extensive study of the use of large-scale kernel approximations in the context of independence testing, contrasting block-based, Nystrom and random Fourier feature approaches. Through a variety of synthetic data experiments, it is demonstrated that our novel large scale methods give comparable performance with existing methods whilst using significantly less computation time and memory.