NASH: Toward End-to-End Neural Architecture for Generative Semantic Hashing

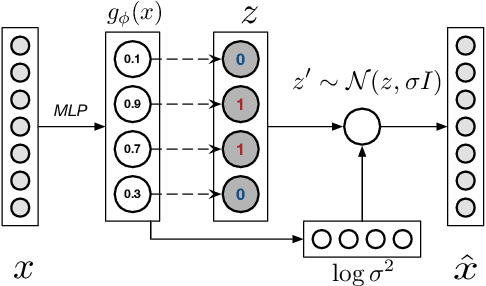
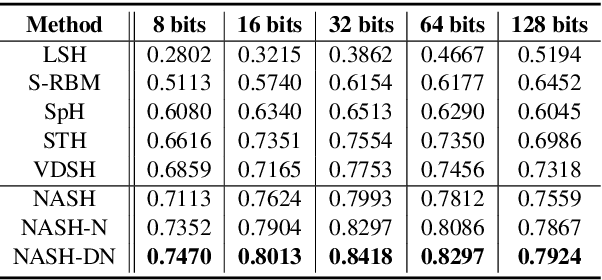
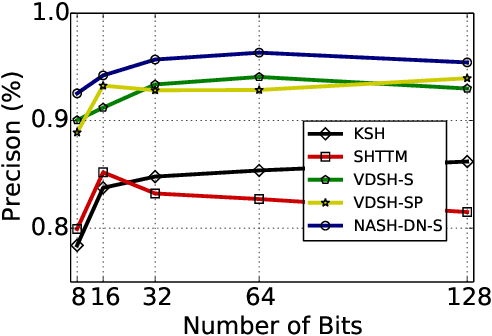
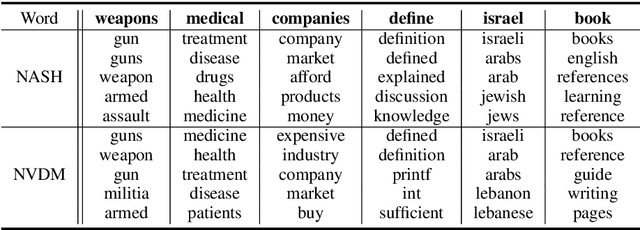
Semantic hashing has become a powerful paradigm for fast similarity search in many information retrieval systems. While fairly successful, previous techniques generally require two-stage training, and the binary constraints are handled ad-hoc. In this paper, we present an end-to-end Neural Architecture for Semantic Hashing (NASH), where the binary hashing codes are treated as Bernoulli latent variables. A neural variational inference framework is proposed for training, where gradients are directly back-propagated through the discrete latent variable to optimize the hash function. We also draw connections between proposed method and rate-distortion theory, which provides a theoretical foundation for the effectiveness of the proposed framework. Experimental results on three public datasets demonstrate that our method significantly outperforms several state-of-the-art models on both unsupervised and supervised scenarios.

Deconvolutional Latent-Variable Model for Text Sequence Matching

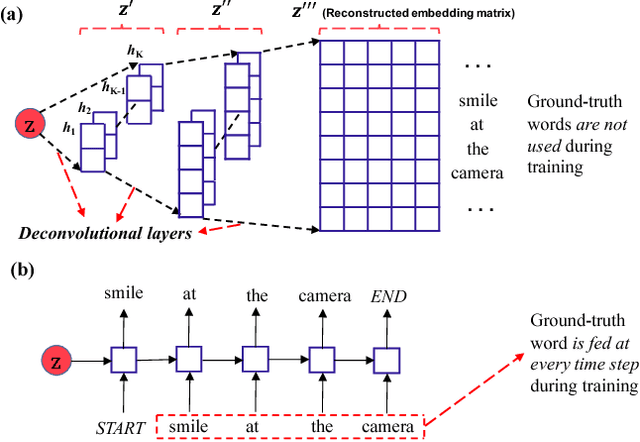
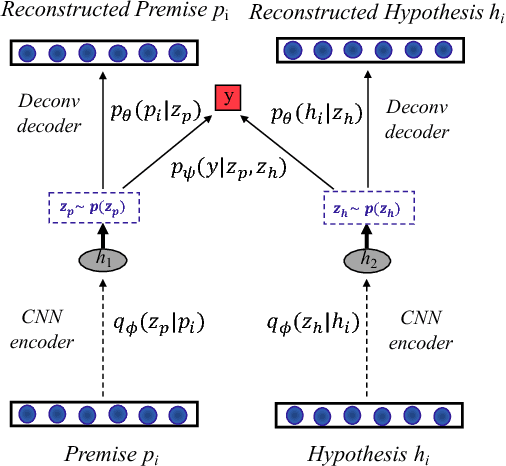
A latent-variable model is introduced for text matching, inferring sentence representations by jointly optimizing generative and discriminative objectives. To alleviate typical optimization challenges in latent-variable models for text, we employ deconvolutional networks as the sequence decoder (generator), providing learned latent codes with more semantic information and better generalization. Our model, trained in an unsupervised manner, yields stronger empirical predictive performance than a decoder based on Long Short-Term Memory (LSTM), with less parameters and considerably faster training. Further, we apply it to text sequence-matching problems. The proposed model significantly outperforms several strong sentence-encoding baselines, especially in the semi-supervised setting.

Symmetric Variational Autoencoder and Connections to Adversarial Learning

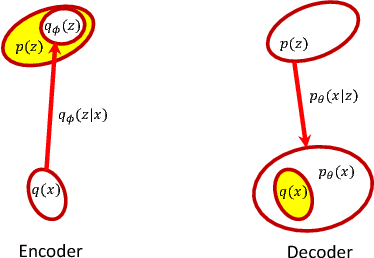
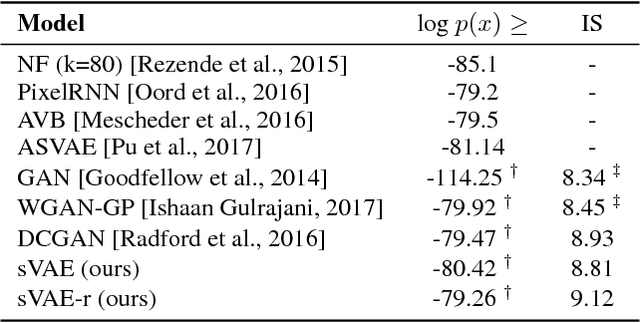
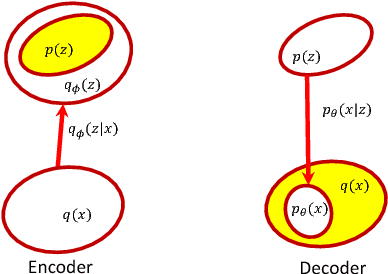
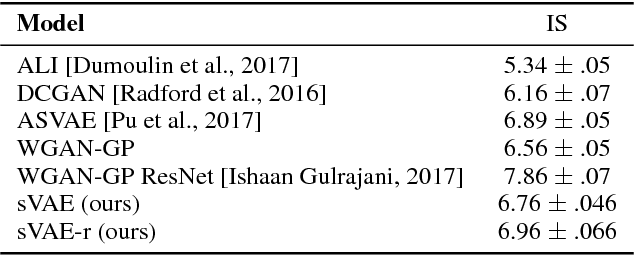
A new form of the variational autoencoder (VAE) is proposed, based on the symmetric Kullback-Leibler divergence. It is demonstrated that learning of the resulting symmetric VAE (sVAE) has close connections to previously developed adversarial-learning methods. This relationship helps unify the previously distinct techniques of VAE and adversarially learning, and provides insights that allow us to ameliorate shortcomings with some previously developed adversarial methods. In addition to an analysis that motivates and explains the sVAE, an extensive set of experiments validate the utility of the approach.

A Probabilistic Framework for Nonlinearities in Stochastic Neural Networks

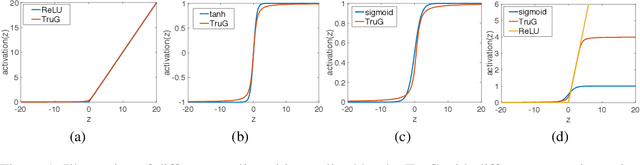
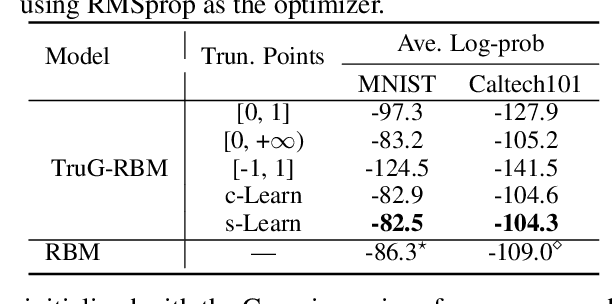
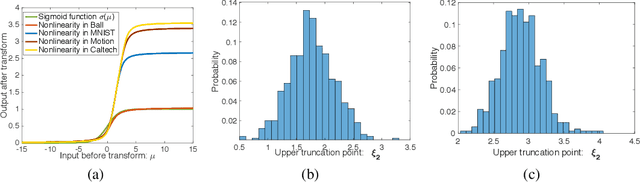
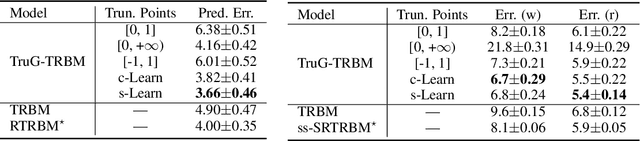
We present a probabilistic framework for nonlinearities, based on doubly truncated Gaussian distributions. By setting the truncation points appropriately, we are able to generate various types of nonlinearities within a unified framework, including sigmoid, tanh and ReLU, the most commonly used nonlinearities in neural networks. The framework readily integrates into existing stochastic neural networks (with hidden units characterized as random variables), allowing one for the first time to learn the nonlinearities alongside model weights in these networks. Extensive experiments demonstrate the performance improvements brought about by the proposed framework when integrated with the restricted Boltzmann machine (RBM), temporal RBM and the truncated Gaussian graphical model (TGGM).

A Convergence Analysis for A Class of Practical Variance-Reduction Stochastic Gradient MCMC

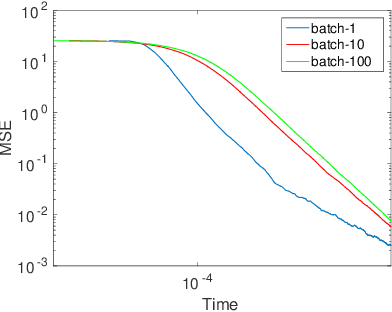
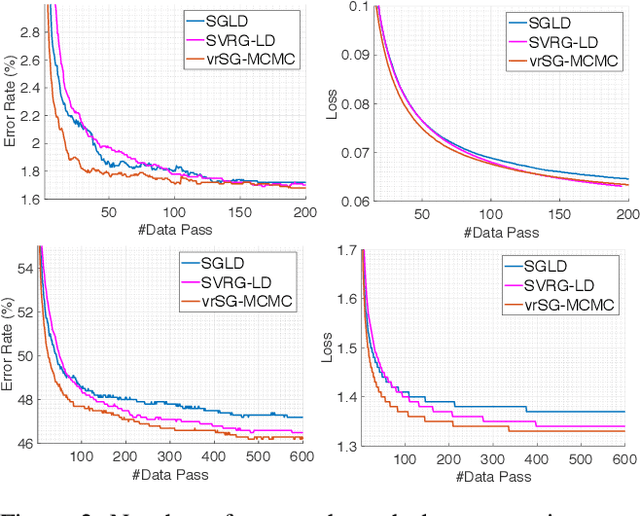
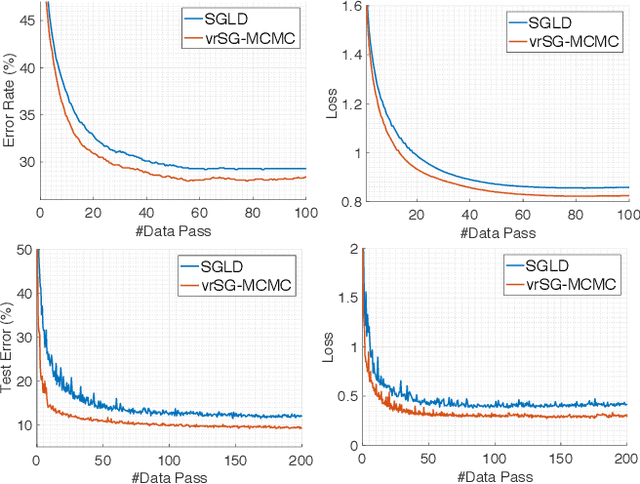
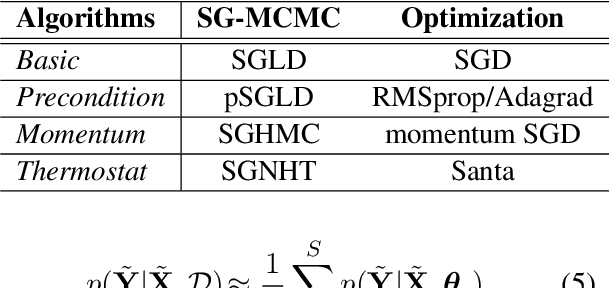
Stochastic gradient Markov Chain Monte Carlo (SG-MCMC) has been developed as a flexible family of scalable Bayesian sampling algorithms. However, there has been little theoretical analysis of the impact of minibatch size to the algorithm's convergence rate. In this paper, we prove that under a limited computational budget/time, a larger minibatch size leads to a faster decrease of the mean squared error bound (thus the fastest one corresponds to using full gradients), which motivates the necessity of variance reduction in SG-MCMC. Consequently, by borrowing ideas from stochastic optimization, we propose a practical variance-reduction technique for SG-MCMC, that is efficient in both computation and storage. We develop theory to prove that our algorithm induces a faster convergence rate than standard SG-MCMC. A number of large-scale experiments, ranging from Bayesian learning of logistic regression to deep neural networks, validate the theory and demonstrate the superiority of the proposed variance-reduction SG-MCMC framework.

Scalable Bayesian Learning of Recurrent Neural Networks for Language Modeling

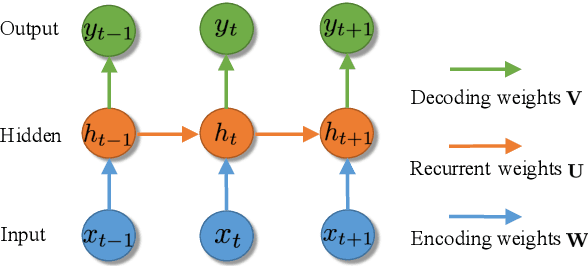
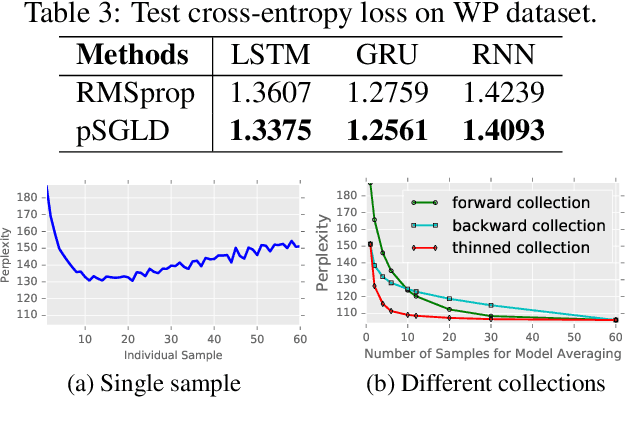
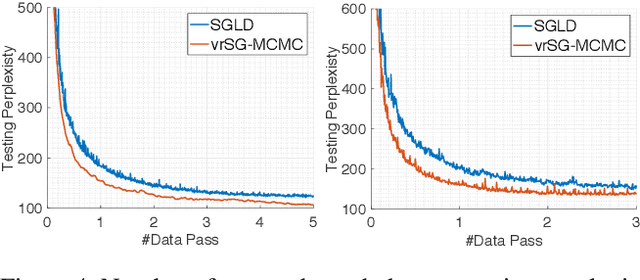
Recurrent neural networks (RNNs) have shown promising performance for language modeling. However, traditional training of RNNs using back-propagation through time often suffers from overfitting. One reason for this is that stochastic optimization (used for large training sets) does not provide good estimates of model uncertainty. This paper leverages recent advances in stochastic gradient Markov Chain Monte Carlo (also appropriate for large training sets) to learn weight uncertainty in RNNs. It yields a principled Bayesian learning algorithm, adding gradient noise during training (enhancing exploration of the model-parameter space) and model averaging when testing. Extensive experiments on various RNN models and across a broad range of applications demonstrate the superiority of the proposed approach over stochastic optimization.

Nonlinear Statistical Learning with Truncated Gaussian Graphical Models

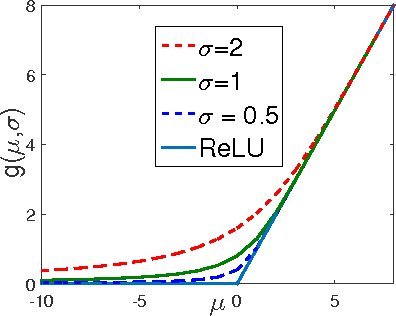
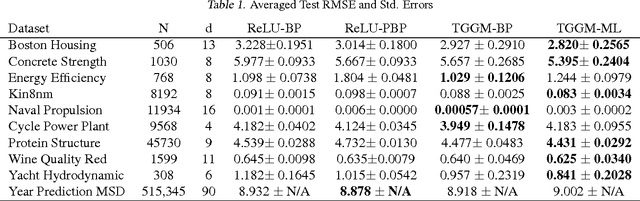
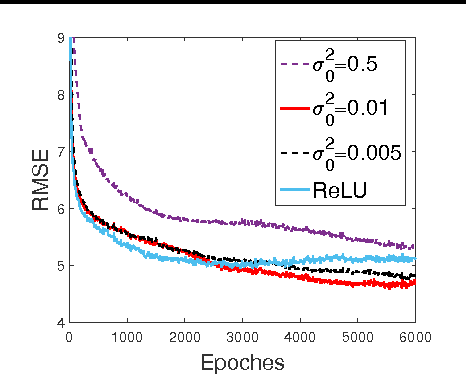
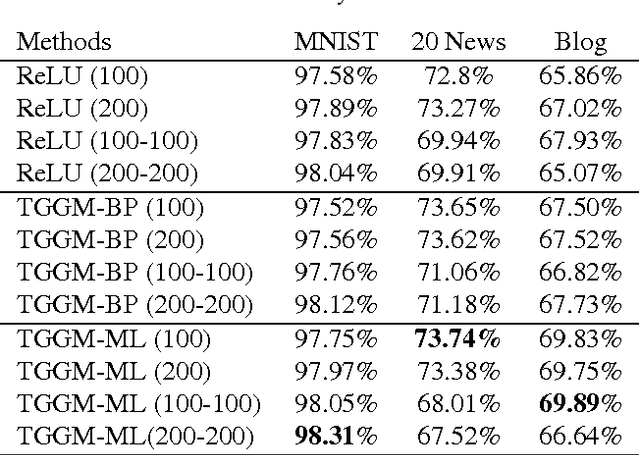
We introduce the truncated Gaussian graphical model (TGGM) as a novel framework for designing statistical models for nonlinear learning. A TGGM is a Gaussian graphical model (GGM) with a subset of variables truncated to be nonnegative. The truncated variables are assumed latent and integrated out to induce a marginal model. We show that the variables in the marginal model are non-Gaussian distributed and their expected relations are nonlinear. We use expectation-maximization to break the inference of the nonlinear model into a sequence of TGGM inference problems, each of which is efficiently solved by using the properties and numerical methods of multivariate Gaussian distributions. We use the TGGM to design models for nonlinear regression and classification, with the performances of these models demonstrated on extensive benchmark datasets and compared to state-of-the-art competing results.

Unsupervised Learning with Truncated Gaussian Graphical Models

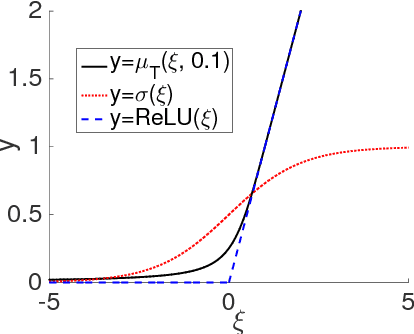
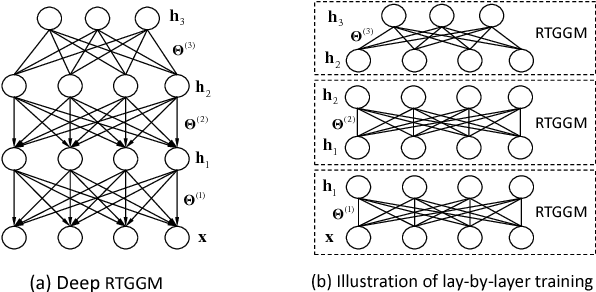
Gaussian graphical models (GGMs) are widely used for statistical modeling, because of ease of inference and the ubiquitous use of the normal distribution in practical approximations. However, they are also known for their limited modeling abilities, due to the Gaussian assumption. In this paper, we introduce a novel variant of GGMs, which relaxes the Gaussian restriction and yet admits efficient inference. Specifically, we impose a bipartite structure on the GGM and govern the hidden variables by truncated normal distributions. The nonlinearity of the model is revealed by its connection to rectified linear unit (ReLU) neural networks. Meanwhile, thanks to the bipartite structure and appealing properties of truncated normals, we are able to train the models efficiently using contrastive divergence. We consider three output constructs, accounting for real-valued, binary and count data. We further extend the model to deep constructions and show that deep models can be used for unsupervised pre-training of rectifier neural networks. Extensive experimental results are provided to validate the proposed models and demonstrate their superiority over competing models.