Traversal Verification for Speculative Tree Decoding

Speculative decoding is a promising approach for accelerating large language models. The primary idea is to use a lightweight draft model to speculate the output of the target model for multiple subsequent timesteps, and then verify them in parallel to determine whether the drafted tokens should be accepted or rejected. To enhance acceptance rates, existing frameworks typically construct token trees containing multiple candidates in each timestep. However, their reliance on token-level verification mechanisms introduces two critical limitations: First, the probability distribution of a sequence differs from that of individual tokens, leading to suboptimal acceptance length. Second, current verification schemes begin from the root node and proceed layer by layer in a top-down manner. Once a parent node is rejected, all its child nodes should be discarded, resulting in inefficient utilization of speculative candidates. This paper introduces Traversal Verification, a novel speculative decoding algorithm that fundamentally rethinks the verification paradigm through leaf-to-root traversal. Our approach considers the acceptance of the entire token sequence from the current node to the root, and preserves potentially valid subsequences that would be prematurely discarded by existing methods. We theoretically prove that the probability distribution obtained through Traversal Verification is identical to that of the target model, guaranteeing lossless inference while achieving substantial acceleration gains. Experimental results across different large language models and multiple tasks show that our method consistently improves acceptance length and throughput over existing methods

Inference for Network Structure and Dynamics from Time Series Data via Graph Neural Network

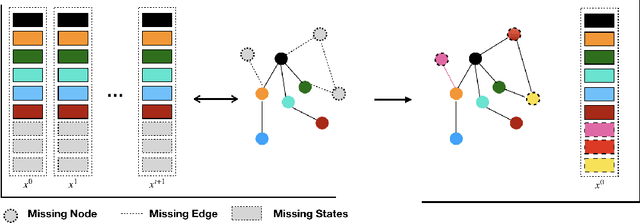
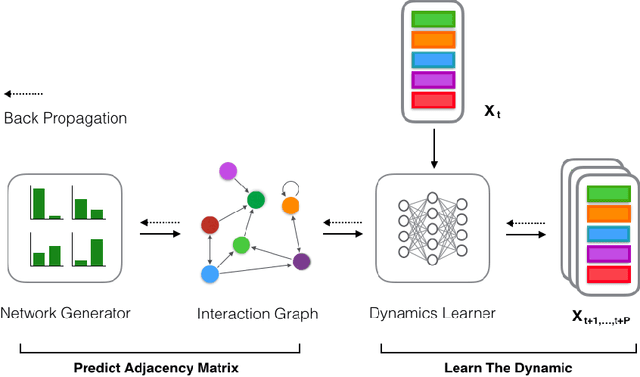
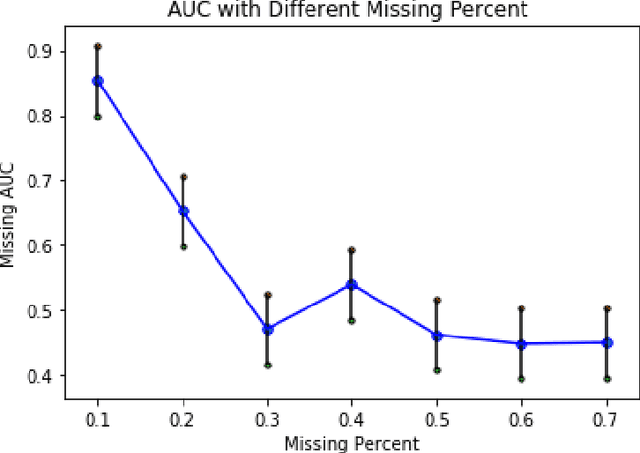
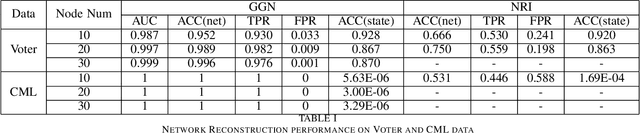
Network structures in various backgrounds play important roles in social, technological, and biological systems. However, the observable network structures in real cases are often incomplete or unavailable due to measurement errors or private protection issues. Therefore, inferring the complete network structure is useful for understanding complex systems. The existing studies have not fully solved the problem of inferring network structure with partial or no information about connections or nodes. In this paper, we tackle the problem by utilizing time series data generated by network dynamics. We regard the network inference problem based on dynamical time series data as a problem of minimizing errors for predicting future states and proposed a novel data-driven deep learning model called Gumbel Graph Network (GGN) to solve the two kinds of network inference problems: Network Reconstruction and Network Completion. For the network reconstruction problem, the GGN framework includes two modules: the dynamics learner and the network generator. For the network completion problem, GGN adds a new module called the States Learner to infer missing parts of the network. We carried out experiments on discrete and continuous time series data. The experiments show that our method can reconstruct up to 100% network structure on the network reconstruction task. While the model can also infer the unknown parts of the structure with up to 90% accuracy when some nodes are missing. And the accuracy decays with the increase of the fractions of missing nodes. Our framework may have wide application areas where the network structure is hard to obtained and the time series data is rich.