Large Deviations for Sequential Tests of Statistical Sequence Matching

We revisit the problem of statistical sequence matching initiated by Unnikrishnan (TIT 2015) and derive theoretical performance guarantees for sequential tests that have bounded expected stopping times. Specifically, in this problem, one is given two databases of sequences and the task is to identify all matched pairs of sequences. In each database, each sequence is generated i.i.d. from a distinct distribution and a pair of sequences is said matched if they are generated from the same distribution. The generating distribution of each sequence is \emph{unknown}. We first consider the case where the number of matches is known and derive the exact exponential decay rate of the mismatch (error) probability, a.k.a. the mismatch exponent, under each hypothesis for optimal sequential tests. Our results reveal the benefit of sequentiality by showing that optimal sequential tests have larger mismatch exponent than fixed-length tests by Zhou \emph{et al.} (TIT 2024). Subsequently, we generalize our achievability result to the case of unknown number of matches. In this case, two additional error probabilities arise: false alarm and false reject probabilities. We propose a corresponding sequential test, show that the test has bounded expected stopping time under certain conditions, and characterize the tradeoff among the exponential decay rates of three error probabilities. Furthermore, we reveal the benefit of sequentiality over the two-step fixed-length test by Zhou \emph{et al.} (TIT 2024) and propose an one-step fixed-length test that has no worse performance than the fixed-length test by Zhou \emph{et al.} (TIT 2024). When specialized to the case where either database contains a single sequence, our results specialize to large deviations of sequential tests for statistical classification, the binary case of which was recently studied by Hsu, Li and Wang (ITW 2022).

Large and Small Deviations for Statistical Sequence Matching

We revisit the problem of statistical sequence matching between two databases of sequences initiated by Unnikrishnan (TIT 2015) and derive theoretical performance guarantees for the generalized likelihood ratio test (GLRT). We first consider the case where the number of matched pairs of sequences between the databases is known. In this case, the task is to accurately find the matched pairs of sequences among all possible matches between the sequences in the two databases. We analyze the performance of the GLRT by Unnikrishnan and explicitly characterize the tradeoff between the mismatch and false reject probabilities under each hypothesis in both large and small deviations regimes. Furthermore, we demonstrate the optimality of Unnikrishnan's GLRT test under the generalized Neyman-Person criterion for both regimes and illustrate our theoretical results via numerical examples. Subsequently, we generalize our achievability analyses to the case where the number of matched pairs is unknown, and an additional error probability needs to be considered. When one of the two databases contains a single sequence, the problem of statistical sequence matching specializes to the problem of multiple classification introduced by Gutman (TIT 1989). For this special case, our result for the small deviations regime strengthens previous result of Zhou, Tan and Motani (Information and Inference 2020) by removing unnecessary conditions on the generating distributions.

3D-TalkEmo: Learning to Synthesize 3D Emotional Talking Head

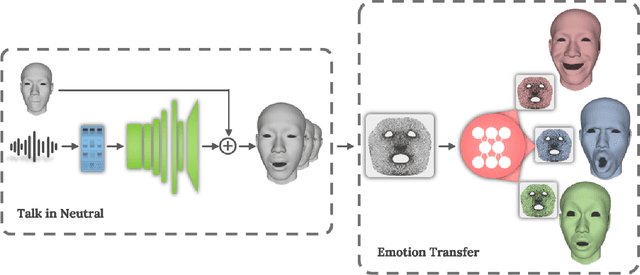
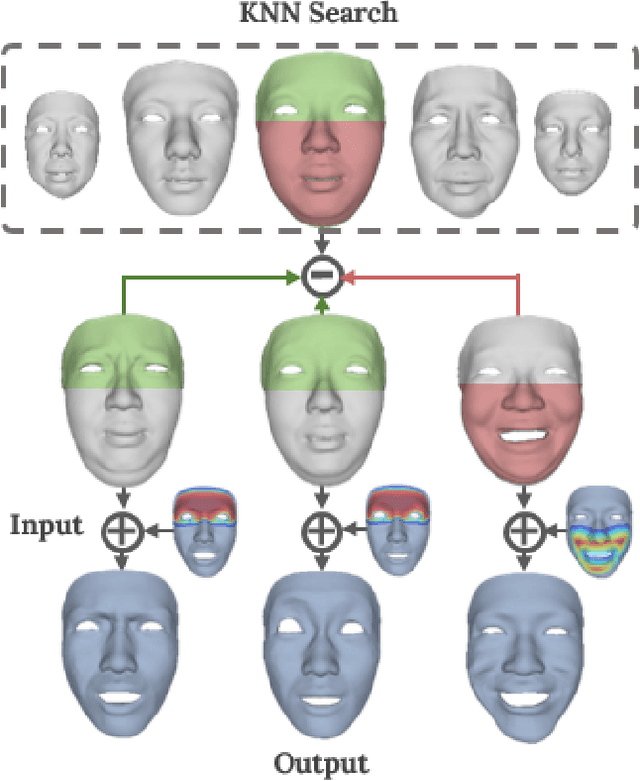
Impressive progress has been made in audio-driven 3D facial animation recently, but synthesizing 3D talking-head with rich emotion is still unsolved. This is due to the lack of 3D generative models and available 3D emotional dataset with synchronized audios. To address this, we introduce 3D-TalkEmo, a deep neural network that generates 3D talking head animation with various emotions. We also create a large 3D dataset with synchronized audios and videos, rich corpus, as well as various emotion states of different persons with the sophisticated 3D face reconstruction methods. In the emotion generation network, we propose a novel 3D face representation structure - geometry map by classical multi-dimensional scaling analysis. It maps the coordinates of vertices on a 3D face to a canonical image plane, while preserving the vertex-to-vertex geodesic distance metric in a least-square sense. This maintains the adjacency relationship of each vertex and holds the effective convolutional structure for the 3D facial surface. Taking a neutral 3D mesh and a speech signal as inputs, the 3D-TalkEmo is able to generate vivid facial animations. Moreover, it provides access to change the emotion state of the animated speaker. We present extensive quantitative and qualitative evaluation of our method, in addition to user studies, demonstrating the generated talking-heads of significantly higher quality compared to previous state-of-the-art methods.