Adaptive Multi-Scale Correlation Meta-Network for Few-Shot Remote Sensing Image Classification

Few-shot learning in remote sensing remains challenging due to three factors: the scarcity of labeled data, substantial domain shifts, and the multi-scale nature of geospatial objects. To address these issues, we introduce Adaptive Multi-Scale Correlation Meta-Network (AMC-MetaNet), a lightweight yet powerful framework with three key innovations: (i) correlation-guided feature pyramids for capturing scale-invariant patterns, (ii) an adaptive channel correlation module (ACCM) for learning dynamic cross-scale relationships, and (iii) correlation-guided meta-learning that leverages correlation patterns instead of conventional prototype averaging. Unlike prior approaches that rely on heavy pre-trained models or transformers, AMC-MetaNet is trained from scratch with only $\sim600K$ parameters, offering $20\times$ fewer parameters than ResNet-18 while maintaining high efficiency ($<50$ms per image inference). AMC-MetaNet achieves up to 86.65\% accuracy in 5-way 5-shot classification on various remote sensing datasets, including EuroSAT, NWPU-RESISC45, UC Merced Land Use, and AID. Our results establish AMC-MetaNet as a computationally efficient, scale-aware framework for real-world few-shot remote sensing.

Regret Lower Bounds for Decentralized Multi-Agent Stochastic Shortest Path Problems

Multi-agent systems (MAS) are central to applications such as swarm robotics and traffic routing, where agents must coordinate in a decentralized manner to achieve a common objective. Stochastic Shortest Path (SSP) problems provide a natural framework for modeling decentralized control in such settings. While the problem of learning in SSP has been extensively studied in single-agent settings, the decentralized multi-agent variant remains largely unexplored. In this work, we take a step towards addressing that gap. We study decentralized multi-agent SSPs (Dec-MASSPs) under linear function approximation, where the transition dynamics and costs are represented using linear models. Applying novel symmetry-based arguments, we identify the structure of optimal policies. Our main contribution is the first regret lower bound for this setting based on the construction of hard-to-learn instances for any number of agents, $n$. Our regret lower bound of $\Omega(\sqrt{K})$, over $K$ episodes, highlights the inherent learning difficulty in Dec-MASSPs. These insights clarify the learning complexity of decentralized control and can further guide the design of efficient learning algorithms in multi-agent systems.

Sample Complexity of Diffusion Model Training Without Empirical Risk Minimizer Access

Diffusion models have demonstrated state-of-the-art performance across vision, language, and scientific domains. Despite their empirical success, prior theoretical analyses of the sample complexity suffer from poor scaling with input data dimension or rely on unrealistic assumptions such as access to exact empirical risk minimizers. In this work, we provide a principled analysis of score estimation, establishing a sample complexity bound of $\widetilde{\mathcal{O}}(\epsilon^{-6})$. Our approach leverages a structured decomposition of the score estimation error into statistical, approximation, and optimization errors, enabling us to eliminate the exponential dependence on neural network parameters that arises in prior analyses. It is the first such result which achieves sample complexity bounds without assuming access to the empirical risk minimizer of score function estimation loss.

Align-Pro: A Principled Approach to Prompt Optimization for LLM Alignment

The alignment of large language models (LLMs) with human values is critical as these models become increasingly integrated into various societal and decision-making processes. Traditional methods, such as reinforcement learning from human feedback (RLHF), achieve alignment by fine-tuning model parameters, but these approaches are often computationally expensive and impractical when models are frozen or inaccessible for parameter modification. In contrast, prompt optimization is a viable alternative to RLHF for LLM alignment. While the existing literature has shown empirical promise of prompt optimization, its theoretical underpinning remains under-explored. We address this gap by formulating prompt optimization as an optimization problem and try to provide theoretical insights into the optimality of such a framework. To analyze the performance of the prompt optimization, we study theoretical suboptimality bounds and provide insights in terms of how prompt optimization depends upon the given prompter and target model. We also provide empirical validation through experiments on various datasets, demonstrating that prompt optimization can effectively align LLMs, even when parameter fine-tuning is not feasible.

Multi-Agent congestion cost minimization with linear function approximation

This work considers multiple agents traversing a network from a source node to the goal node. The cost to an agent for traveling a link has a private as well as a congestion component. The agent's objective is to find a path to the goal node with minimum overall cost in a decentralized way. We model this as a fully decentralized multi-agent reinforcement learning problem and propose a novel multi-agent congestion cost minimization (MACCM) algorithm. Our MACCM algorithm uses linear function approximations of transition probabilities and the global cost function. In the absence of a central controller and to preserve privacy, agents communicate the cost function parameters to their neighbors via a time-varying communication network. Moreover, each agent maintains its estimate of the global state-action value, which is updated via a multi-agent extended value iteration (MAEVI) sub-routine. We show that our MACCM algorithm achieves a sub-linear regret. The proof requires the convergence of cost function parameters, the MAEVI algorithm, and analysis of the regret bounds induced by the MAEVI triggering condition for each agent. We implement our algorithm on a two node network with multiple links to validate it. We first identify the optimal policy, the optimal number of agents going to the goal node in each period. We observe that the average regret is close to zero for 2 and 3 agents. The optimal policy captures the trade-off between the minimum cost of staying at a node and the congestion cost of going to the goal node. Our work is a generalization of learning the stochastic shortest path problem.

Multi-agent Natural Actor-critic Reinforcement Learning Algorithms

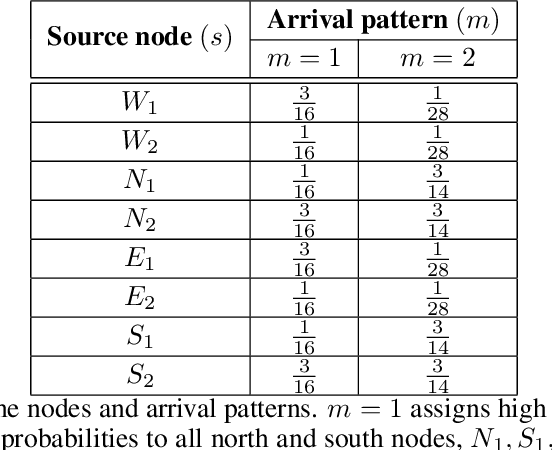
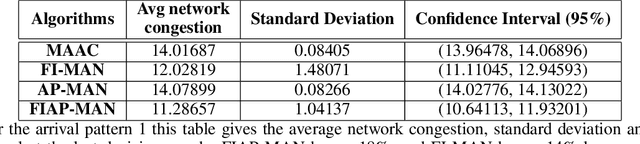
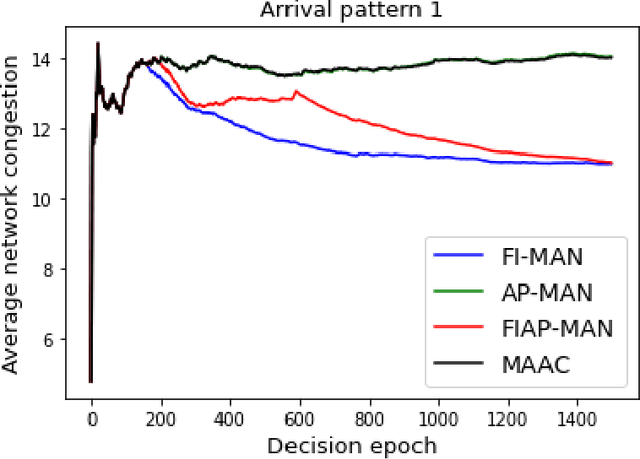
Both single-agent and multi-agent actor-critic algorithms are an important class of Reinforcement Learning algorithms. In this work, we propose three fully decentralized multi-agent natural actor-critic (MAN) algorithms. The agents' objective is to collectively learn a joint policy that maximizes the sum of averaged long-term returns of these agents. In the absence of a central controller, agents communicate the information to their neighbors via a time-varying communication network while preserving privacy. We prove the convergence of all the 3 MAN algorithms to a globally asymptotically stable point of the ODE corresponding to the actor update; these use linear function approximations. We use the Fisher information matrix to obtain the natural gradients. The Fisher information matrix captures the curvature of the Kullback-Leibler (KL) divergence between polices at successive iterates. We also show that the gradient of this KL divergence between policies of successive iterates is proportional to the objective function's gradient. Our MAN algorithms indeed use this \emph{representation} of the objective function's gradient. Under certain conditions on the Fisher information matrix, we prove that at each iterate, the optimal value via MAN algorithms can be better than that of the multi-agent actor-critic (MAAC) algorithm using the standard gradients. To validate the usefulness of our proposed algorithms, we implement all the 3 MAN algorithms on a bi-lane traffic network to reduce the average network congestion. We observe an almost 25% reduction in the average congestion in 2 MAN algorithms; the average congestion in another MAN algorithm is on par with the MAAC algorithm. We also consider a generic 15 agent MARL; the performance of the MAN algorithms is again as good as the MAAC algorithm. We attribute the better performance of the MAN algorithms to their use of the above representation.

On Feature Interactions Identified by Shapley Values of Binary Classification Games

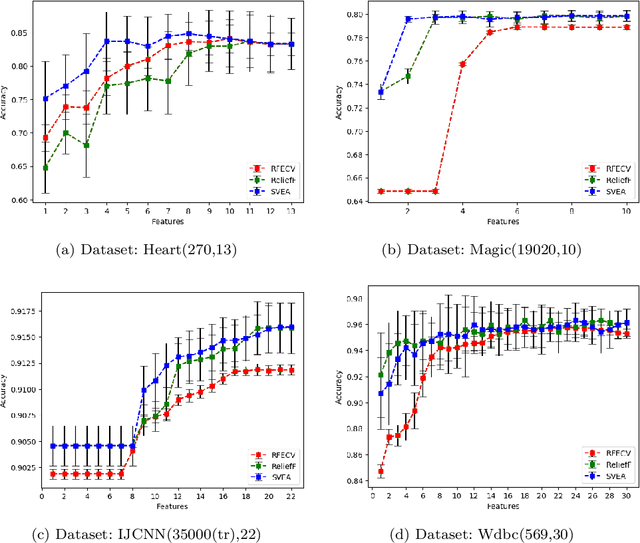
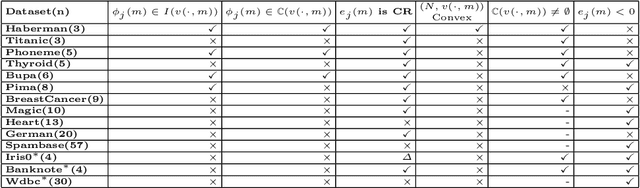
For feature selection and related problems, we introduce the notion of classification game, a cooperative game, with features as players and hinge loss based characteristic function and relate a feature's contribution to Shapley value based error apportioning (SVEA) of total training error. Our major contribution is ($\star$) to show that for any dataset the threshold 0 on SVEA value identifies feature subset whose joint interactions for label prediction is significant or those features that span a subspace where the data is predominantly lying. In addition, our scheme ($\star$) identifies the features on which Bayes classifier doesn't depend but any surrogate loss function based finite sample classifier does; this contributes to the excess $0$-$1$ risk of such a classifier, ($\star$) estimates unknown true hinge risk of a feature, and ($\star$) relate the stability property of an allocation and negative valued SVEA by designing the analogue of core of classification game. Due to Shapley value's computationally expensive nature, we build on a known Monte Carlo based approximation algorithm that computes characteristic function (Linear Programs) only when needed. We address the potential sample bias problem in feature selection by providing interval estimates for SVEA values obtained from multiple sub-samples. We illustrate all the above aspects on various synthetic and real datasets and show that our scheme achieves better results than existing recursive feature elimination technique and ReliefF in most cases. Our theoretically grounded classification game in terms of well defined characteristic function offers interpretability and explainability of our framework, including identification of important features.