RRLS : Robust Reinforcement Learning Suite

Robust reinforcement learning is the problem of learning control policies that provide optimal worst-case performance against a span of adversarial environments. It is a crucial ingredient for deploying algorithms in real-world scenarios with prevalent environmental uncertainties and has been a long-standing object of attention in the community, without a standardized set of benchmarks. This contribution endeavors to fill this gap. We introduce the Robust Reinforcement Learning Suite (RRLS), a benchmark suite based on Mujoco environments. RRLS provides six continuous control tasks with two types of uncertainty sets for training and evaluation. Our benchmark aims to standardize robust reinforcement learning tasks, facilitating reproducible and comparable experiments, in particular those from recent state-of-the-art contributions, for which we demonstrate the use of RRLS. It is also designed to be easily expandable to new environments. The source code is available at \href{https://github.com/SuReLI/RRLS}{https://github.com/SuReLI/RRLS}.

Time-Constrained Robust MDPs

Robust reinforcement learning is essential for deploying reinforcement learning algorithms in real-world scenarios where environmental uncertainty predominates. Traditional robust reinforcement learning often depends on rectangularity assumptions, where adverse probability measures of outcome states are assumed to be independent across different states and actions. This assumption, rarely fulfilled in practice, leads to overly conservative policies. To address this problem, we introduce a new time-constrained robust MDP (TC-RMDP) formulation that considers multifactorial, correlated, and time-dependent disturbances, thus more accurately reflecting real-world dynamics. This formulation goes beyond the conventional rectangularity paradigm, offering new perspectives and expanding the analytical framework for robust RL. We propose three distinct algorithms, each using varying levels of environmental information, and evaluate them extensively on continuous control benchmarks. Our results demonstrate that these algorithms yield an efficient tradeoff between performance and robustness, outperforming traditional deep robust RL methods in time-constrained environments while preserving robustness in classical benchmarks. This study revisits the prevailing assumptions in robust RL and opens new avenues for developing more practical and realistic RL applications.

Bootstrapping Expectiles in Reinforcement Learning

Many classic Reinforcement Learning (RL) algorithms rely on a Bellman operator, which involves an expectation over the next states, leading to the concept of bootstrapping. To introduce a form of pessimism, we propose to replace this expectation with an expectile. In practice, this can be very simply done by replacing the $L_2$ loss with a more general expectile loss for the critic. Introducing pessimism in RL is desirable for various reasons, such as tackling the overestimation problem (for which classic solutions are double Q-learning or the twin-critic approach of TD3) or robust RL (where transitions are adversarial). We study empirically these two cases. For the overestimation problem, we show that the proposed approach, ExpectRL, provides better results than a classic twin-critic. On robust RL benchmarks, involving changes of the environment, we show that our approach is more robust than classic RL algorithms. We also introduce a variation of ExpectRL combined with domain randomization which is competitive with state-of-the-art robust RL agents. Eventually, we also extend \ExpectRL with a mechanism for choosing automatically the expectile value, that is the degree of pessimism

VITS : Variational Inference Thomson Sampling for contextual bandits

In this paper, we introduce and analyze a variant of the Thompson sampling (TS) algorithm for contextual bandits. At each round, traditional TS requires samples from the current posterior distribution, which is usually intractable. To circumvent this issue, approximate inference techniques can be used and provide samples with distribution close to the posteriors. However, current approximate techniques yield to either poor estimation (Laplace approximation) or can be computationally expensive (MCMC methods, Ensemble sampling...). In this paper, we propose a new algorithm, Varational Inference Thompson sampling VITS, based on Gaussian Variational Inference. This scheme provides powerful posterior approximations which are easy to sample from, and is computationally efficient, making it an ideal choice for TS. In addition, we show that VITS achieves a sub-linear regret bound of the same order in the dimension and number of round as traditional TS for linear contextual bandit. Finally, we demonstrate experimentally the effectiveness of VITS on both synthetic and real world datasets.

Towards Minimax Optimality of Model-based Robust Reinforcement Learning

We study the sample complexity of obtaining an $\epsilon$-optimal policy in \emph{Robust} discounted Markov Decision Processes (RMDPs), given only access to a generative model of the nominal kernel. This problem is widely studied in the non-robust case, and it is known that any planning approach applied to an empirical MDP estimated with $\tilde{\mathcal{O}}(\frac{H^3 \mid S \mid\mid A \mid}{\epsilon^2})$ samples provides an $\epsilon$-optimal policy, which is minimax optimal. Results in the robust case are much more scarce. For $sa$- (resp $s$-)rectangular uncertainty sets, the best known sample complexity is $\tilde{\mathcal{O}}(\frac{H^4 \mid S \mid^2\mid A \mid}{\epsilon^2})$ (resp. $\tilde{\mathcal{O}}(\frac{H^4 \mid S \mid^2\mid A \mid^2}{\epsilon^2})$), for specific algorithms and when the uncertainty set is based on the total variation (TV), the KL or the Chi-square divergences. In this paper, we consider uncertainty sets defined with an $L_p$-ball (recovering the TV case), and study the sample complexity of \emph{any} planning algorithm (with high accuracy guarantee on the solution) applied to an empirical RMDP estimated using the generative model. In the general case, we prove a sample complexity of $\tilde{\mathcal{O}}(\frac{H^4 \mid S \mid\mid A \mid}{\epsilon^2})$ for both the $sa$- and $s$-rectangular cases (improvements of $\mid S \mid$ and $\mid S \mid\mid A \mid$ respectively). When the size of the uncertainty is small enough, we improve the sample complexity to $\tilde{\mathcal{O}}(\frac{H^3 \mid S \mid\mid A \mid }{\epsilon^2})$, recovering the lower-bound for the non-robust case for the first time and a robust lower-bound when the size of the uncertainty is small enough.

Robust Reinforcement Learning with Distributional Risk-averse formulation

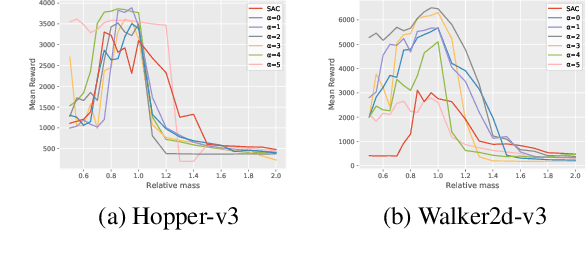
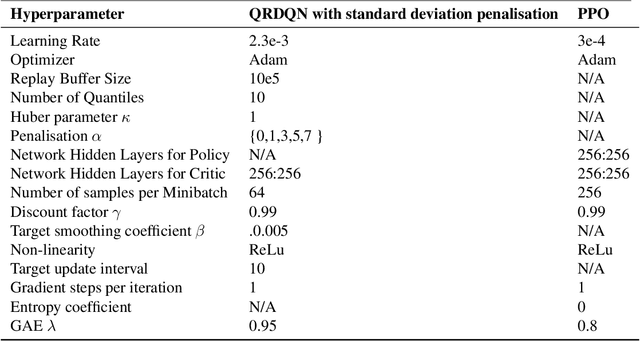
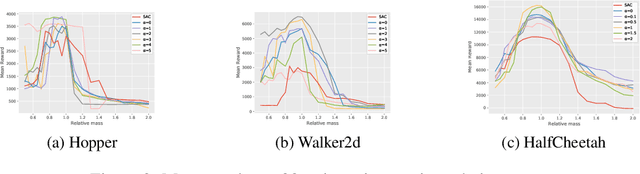
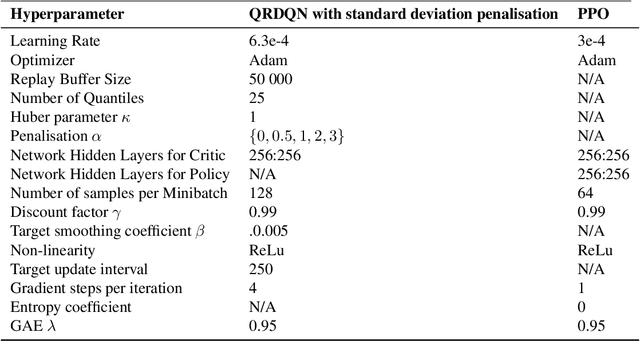
Robust Reinforcement Learning tries to make predictions more robust to changes in the dynamics or rewards of the system. This problem is particularly important when the dynamics and rewards of the environment are estimated from the data. In this paper, we approximate the Robust Reinforcement Learning constrained with a $\Phi$-divergence using an approximate Risk-Averse formulation. We show that the classical Reinforcement Learning formulation can be robustified using standard deviation penalization of the objective. Two algorithms based on Distributional Reinforcement Learning, one for discrete and one for continuous action spaces are proposed and tested in a classical Gym environment to demonstrate the robustness of the algorithms.