Analyzing Closed-loop Training Techniques for Realistic Traffic Agent Models in Autonomous Highway Driving Simulations

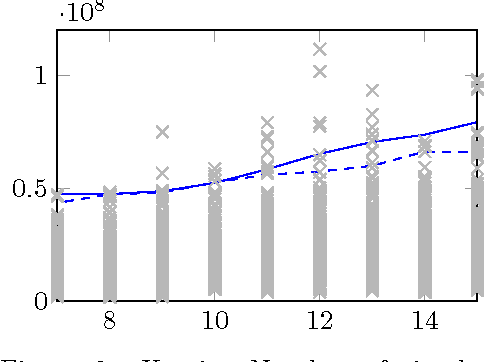
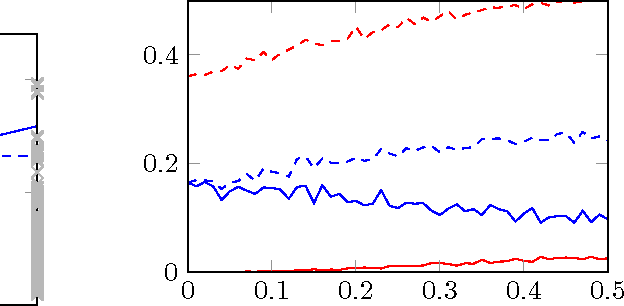
Simulation plays a crucial role in the rapid development and safe deployment of autonomous vehicles. Realistic traffic agent models are indispensable for bridging the gap between simulation and the real world. Many existing approaches for imitating human behavior are based on learning from demonstration. However, these approaches are often constrained by focusing on individual training strategies. Therefore, to foster a broader understanding of realistic traffic agent modeling, in this paper, we provide an extensive comparative analysis of different training principles, with a focus on closed-loop methods for highway driving simulation. We experimentally compare (i) open-loop vs. closed-loop multi-agent training, (ii) adversarial vs. deterministic supervised training, (iii) the impact of reinforcement losses, and (iv) the impact of training alongside log-replayed agents to identify suitable training techniques for realistic agent modeling. Furthermore, we identify promising combinations of different closed-loop training methods.

On Learning the Tail Quantiles of Driving Behavior Distributions via Quantile Regression and Flows

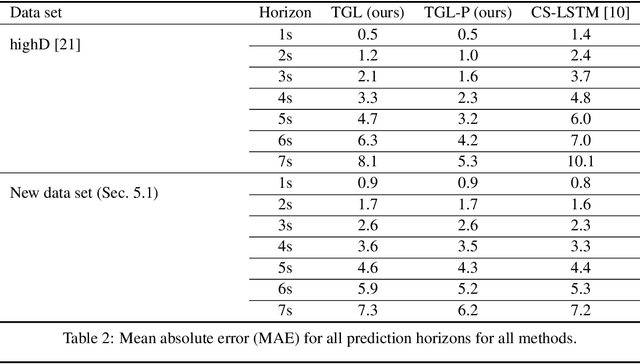
Towards safe autonomous driving (AD), we consider the problem of learning models that accurately capture the diversity and tail quantiles of human driver behavior probability distributions, in interaction with an AD vehicle. Such models, which predict drivers' continuous actions from their states, are particularly relevant for closing the gap between AD simulation and reality. To this end, we adapt two flexible frameworks for this setting that avoid strong distributional assumptions: (1)~quantile regression (based on the titled absolute loss), and (2)~autoregressive quantile flows (a version of normalizing flows). Training happens in a behavior cloning-fashion. We evaluate our approach in a one-step prediction, as well as in multi-step simulation rollouts. We use the highD dataset consisting of driver trajectories on several highways. We report quantitative results using the tilted absolute loss as metric, give qualitative examples showing that realistic extremal behavior can be learned, and discuss the main insights.

Fail-Safe Generative Adversarial Imitation Learning

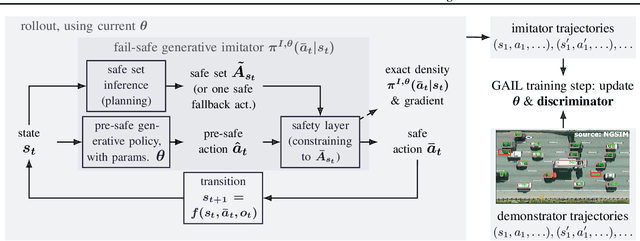
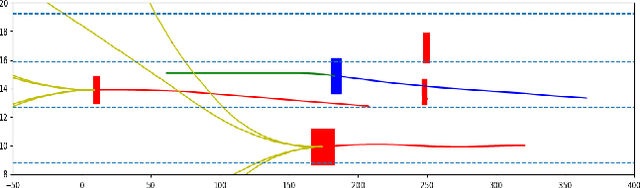
For flexible yet safe imitation learning (IL), we propose a modular approach that uses a generative imitator policy with a safety layer, has an overall explicit density/gradient, can therefore be end-to-end trained using generative adversarial IL (GAIL), and comes with theoretical worst-case safety/robustness guarantees. The safety layer's exact density comes from using a countable non-injective gluing of piecewise differentiable injections and the change-of-variables formula. The safe set (into which the safety layer maps) is inferred by sampling actions and their potential future fail-safe fallback continuations, together with Lipschitz continuity and convexity arguments. We also provide theoretical bounds showing the advantage of using the safety layer already during training (imitation error linear in the horizon) compared to only using it at test time (quadratic error). In an experiment on challenging real-world driver interaction data, we empirically demonstrate tractability, safety and imitation performance of our approach.

Multiagent trajectory models via game theory and implicit layer-based learning

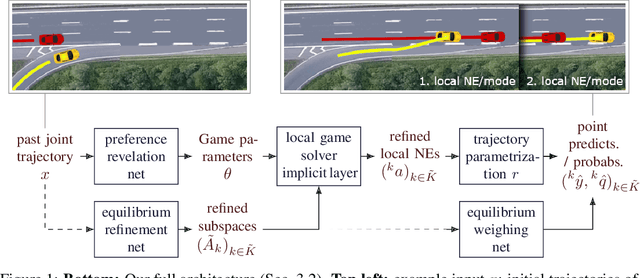
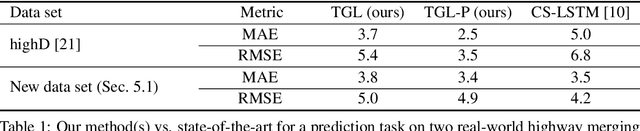
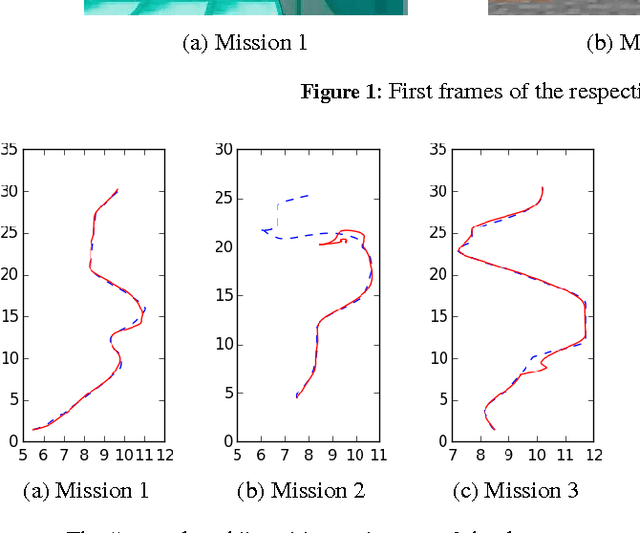
For prediction of interacting agents' trajectories, we propose an end-to-end trainable architecture that hybridizes neural nets with game-theoretic reasoning, has interpretable intermediate representations, and transfers to robust downstream decision making. It combines (1) a differentiable implicit layer that maps preferences to local Nash equilibria with (2) a learned equilibrium refinement concept and (3) a learned preference revelation net, given initial trajectories as input. This is accompanied by a new class of continuous potential games. We provide theoretical results for explicit gradients and soundness, and several measures to ensure tractability. In experiments, we evaluate our approach on two real-world data sets, where we predict highway driver merging trajectories, and on a simple decision-making transfer task.

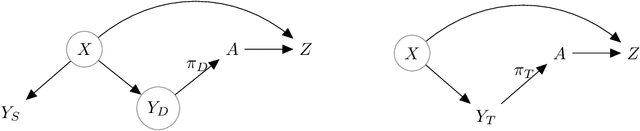
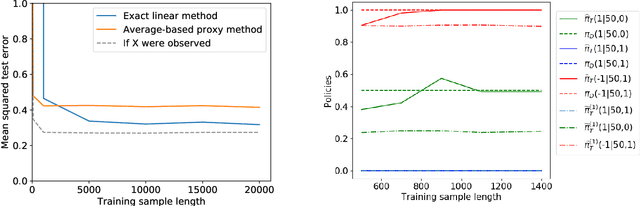
Causal Transfer for Imitation Learning and Decision Making under Sensor-shift

Learning from demonstrations (LfD) is an efficient paradigm to train AI agents. But major issues arise when there are differences between (a) the demonstrator's own sensory input, (b) our sensors that observe the demonstrator and (c) the sensory input of the agent we train. In this paper, we propose a causal model-based framework for transfer learning under such "sensor-shifts", for two common LfD tasks: (1) inferring the effect of the demonstrator's actions and (2) imitation learning. First we rigorously analyze, on the population-level, to what extent the relevant underlying mechanisms (the action effects and the demonstrator policy) can be identified and transferred from the available observations together with prior knowledge of sensor characteristics. And we device an algorithm to infer these mechanisms. Then we introduce several proxy methods which are easier to calculate, estimate from finite data and interpret than the exact solutions, alongside theoretical bounds on their closeness to the exact ones. We validate our two main methods on simulated and semi-real world data.

Coordination via predictive assistants: time series algorithms and game-theoretic analysis

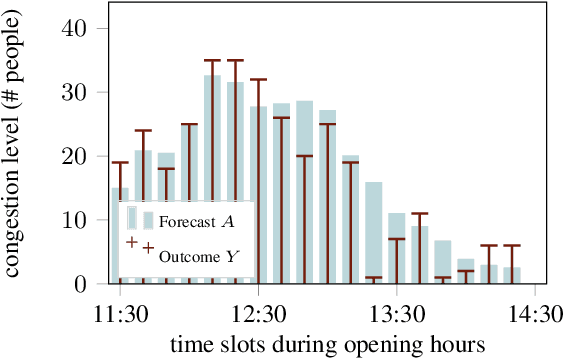
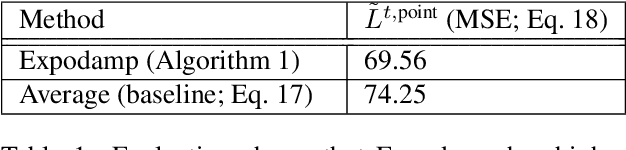
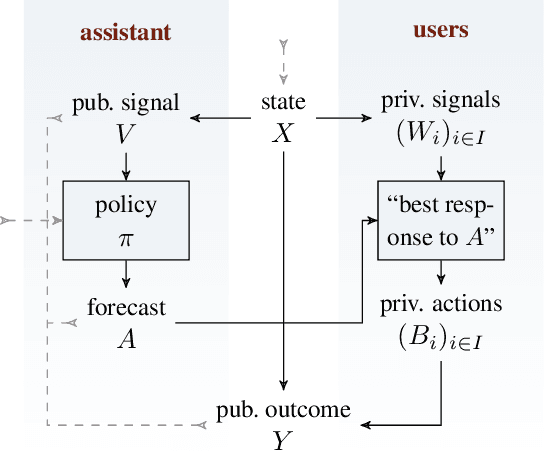
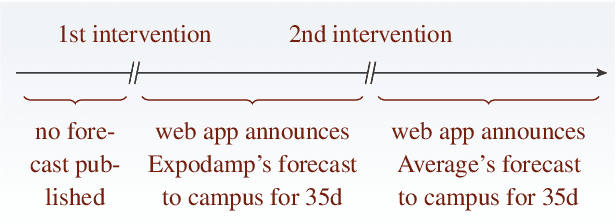
We study data-driven assistants that provide congestion forecasts to users of crowded facilities (roads, cafeterias, etc.), to support coordination between them. Having multiple agents and feedback loops from predictions to outcomes, new problems arise in terms of choosing (1) objective and (2) algorithms for such assistants. Addressing (1), we pick classical prediction accuracy as objective and establish general conditions under which optimizing it is equivalent to "solving" the coordination problem in an idealized game-theoretic sense -- selecting a certain Bayesian Nash equilibrium (BNE). Then we prove the existence of an assistant-based "solution" even for large-scale (nonatomic), aggregated settings. This entails a new BNE existence result. Addressing (2), we propose an exponential smoothing-based algorithm on time series data. We prove its optimality w.r.t.\ the prediction objective under a state-space model for the large-scale setting. We also provide a proof-of-concept algorithm and convergence guarantees for a small-scale, non-aggregated setting. We validate our algorithm in a large-scale experiment in a real cafeteria.

Causal inference for cloud computing

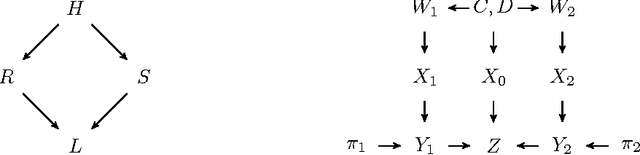
Cloud computing involves complex technical and economical systems and interactions. This brings about various challenges, two of which are: (1) debugging and control of computing systems with the help of sandbox experiments, and (2) prediction of the cost of "spot" resources for decision making of cloud clients. In this paper, we formalize debugging by counterfactual probabilities and control by post-(soft-)interventional probabilities. We prove that counterfactuals can approximately be calculated from a "stochastic" graphical causal model (while they are originally defined only for "deterministic" functional causal models), and based on this sketch an approach to address problem (1). To address problem (2), we formalize bidding by post-(soft-)interventional probabilities and present a simple mathematical result on approximate integration of "incomplete" conditional probability distributions. We show how this can be used by cloud clients to trade off privacy against predictability of the outcome of their bidding actions in a toy scenario. We report experiments on simulated and real data.

Experimental and causal view on information integration in autonomous agents

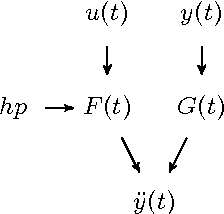
The amount of digitally available but heterogeneous information about the world is remarkable, and new technologies such as self-driving cars, smart homes, or the internet of things may further increase it. In this paper we present preliminary ideas about certain aspects of the problem of how such heterogeneous information can be harnessed by autonomous agents. After discussing potentials and limitations of some existing approaches, we investigate how \emph{experiments} can help to obtain a better understanding of the problem. Specifically, we present a simple agent that integrates video data from a different agent, and implement and evaluate a version of it on the novel experimentation platform \emph{Malmo}. The focus of a second investigation is on how information about the hardware of different agents, the agents' sensory data, and \emph{causal} information can be utilized for knowledge transfer between agents and subsequently more data-efficient decision making. Finally, we discuss potential future steps w.r.t.\ theory and experimentation, and formulate open questions.

Causal Inference by Identification of Vector Autoregressive Processes with Hidden Components

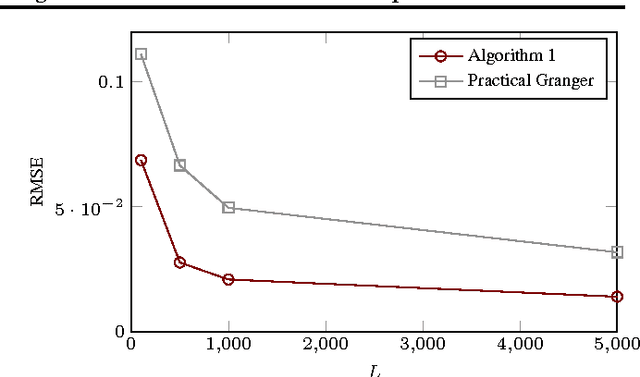
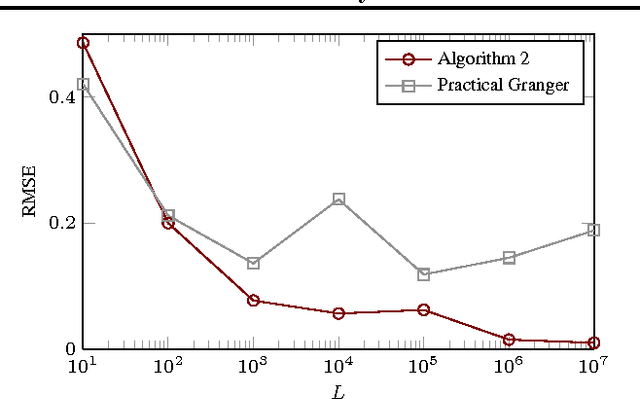
A widely applied approach to causal inference from a non-experimental time series $X$, often referred to as "(linear) Granger causal analysis", is to regress present on past and interpret the regression matrix $\hat{B}$ causally. However, if there is an unmeasured time series $Z$ that influences $X$, then this approach can lead to wrong causal conclusions, i.e., distinct from those one would draw if one had additional information such as $Z$. In this paper we take a different approach: We assume that $X$ together with some hidden $Z$ forms a first order vector autoregressive (VAR) process with transition matrix $A$, and argue why it is more valid to interpret $A$ causally instead of $\hat{B}$. Then we examine under which conditions the most important parts of $A$ are identifiable or almost identifiable from only $X$. Essentially, sufficient conditions are (1) non-Gaussian, independent noise or (2) no influence from $X$ to $Z$. We present two estimation algorithms that are tailored towards conditions (1) and (2), respectively, and evaluate them on synthetic and real-world data. We discuss how to check the model using $X$.