Properties of the After Kernel
Paper and Code
May 27, 2021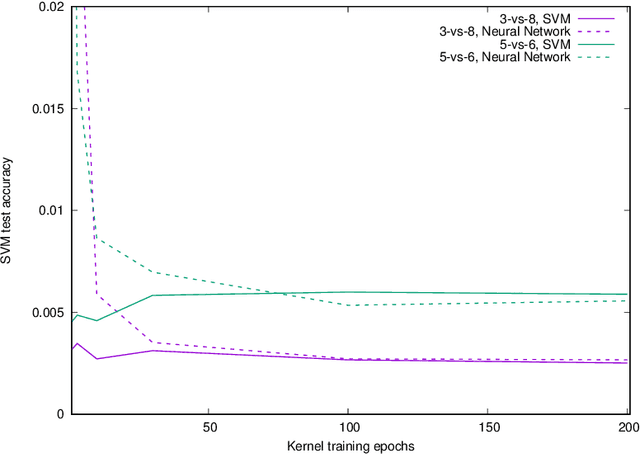
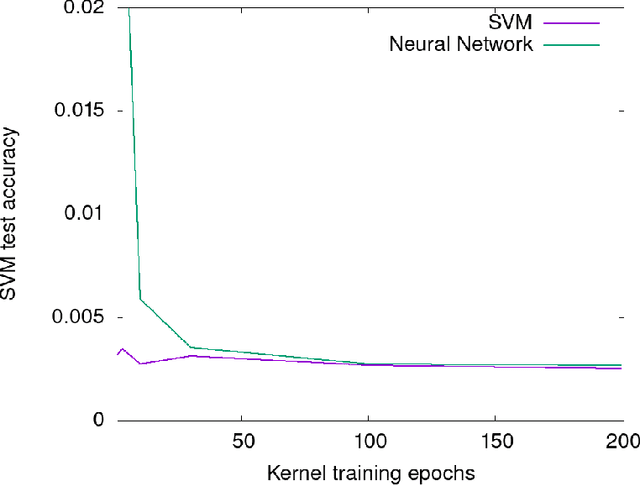
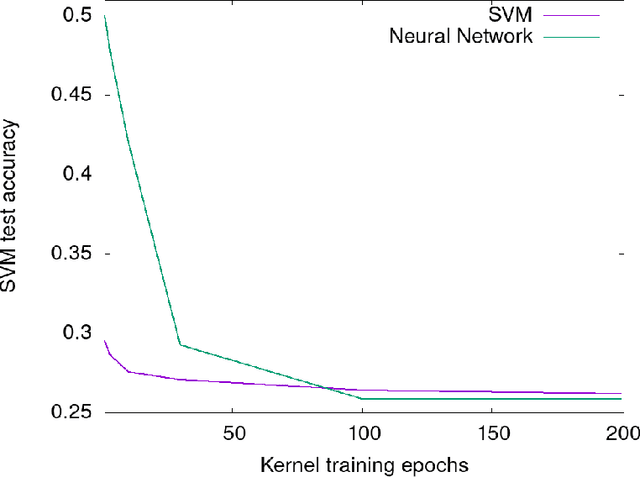
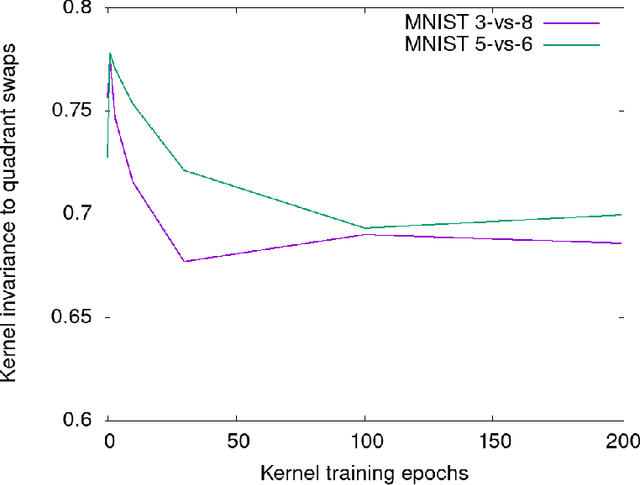
The Neural Tangent Kernel (NTK) is the wide-network limit of a kernel defined using neural networks at initialization, whose embedding is the gradient of the output of the network with respect to its parameters. We study the "after kernel", which is defined using the same embedding, except after training, for neural networks with standard architectures, on binary classification problems extracted from MNIST and CIFAR-10, trained using SGD in a standard way. For some dataset-architecture pairs, after a few epochs of neural network training, a hard-margin SVM using the network's after kernel is much more accurate than when the network's initial kernel is used. For networks with an architecture similar to VGG, the after kernel is more "global", in the sense that it is less invariant to transformations of input images that disrupt the global structure of the image while leaving the local statistics largely intact. For fully connected networks, the after kernel is less global in this sense. The after kernel tends to be more invariant to small shifts, rotations and zooms; data augmentation does not improve these invariances. The (finite approximation to the) conjugate kernel, obtained using the last layer of hidden nodes, sometimes, but not always, provides a good approximation to the NTK and the after kernel.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge