EEG Foundation Challenge: From Cross-Task to Cross-Subject EEG Decoding

Current electroencephalogram (EEG) decoding models are typically trained on small numbers of subjects performing a single task. Here, we introduce a large-scale, code-submission-based competition comprising two challenges. First, the Transfer Challenge asks participants to build and test a model that can zero-shot decode new tasks and new subjects from their EEG data. Second, the Psychopathology factor prediction Challenge asks participants to infer subject measures of mental health from EEG data. For this, we use an unprecedented, multi-terabyte dataset of high-density EEG signals (128 channels) recorded from over 3,000 child to young adult subjects engaged in multiple active and passive tasks. We provide several tunable neural network baselines for each of these two challenges, including a simple network and demographic-based regression models. Developing models that generalise across tasks and individuals will pave the way for ML network architectures capable of adapting to EEG data collected from diverse tasks and individuals. Similarly, predicting mental health-relevant personality trait values from EEG might identify objective biomarkers useful for clinical diagnosis and design of personalised treatment for psychological conditions. Ultimately, the advances spurred by this challenge could contribute to the development of computational psychiatry and useful neurotechnology, and contribute to breakthroughs in both fundamental neuroscience and applied clinical research.

FKreg: A MATLAB toolbox for fast Multivariate Kernel Regression

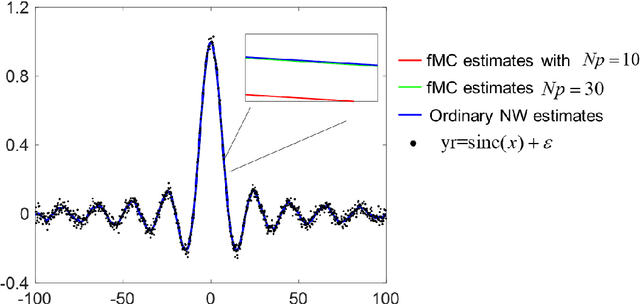
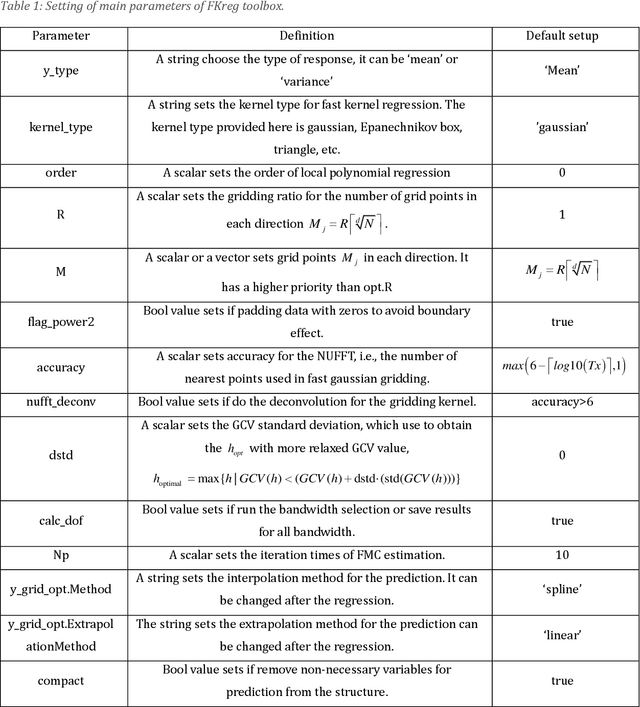
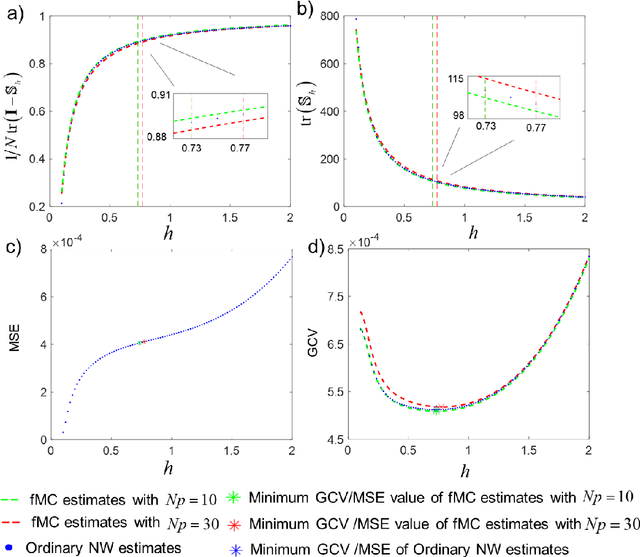
Kernel smooth is the most fundamental technique for data density and regression estimation. However, time-consuming is the biggest obstacle for the application that the direct evaluation of kernel smooth for $N$ samples needs ${O}\left( {{N}^{2}} \right)$ operations. People have developed fast smooth algorithms using the idea of binning with FFT. Unfortunately, the accuracy is not controllable, and the implementation for multivariable and its bandwidth selection for the fast method is not available. Hence, we introduce a new MATLAB toolbox for fast multivariate kernel regression with the idea of non-uniform FFT (NUFFT), which implemented the algorithm for $M$ gridding points with ${O}\left( N+M\log M \right)$ complexity and accuracy controllability. The bandwidth selection problem utilizes the Fast Monte-Carlo algorithm to estimate the degree of freedom (DF), saving enormous cross-validation time even better when data share the same grid space for multiple regression. Up to now, this is the first toolbox for fast-binning high-dimensional kernel regression. Moreover, the estimation for local polynomial regression, the conditional variance for the heteroscedastic model, and the complex-valued datasets are also implemented in this toolbox. The performance is demonstrated with simulations and an application on the quantitive EEG.