A Scalable Combinatorial Solver for Elastic Geometrically Consistent 3D Shape Matching

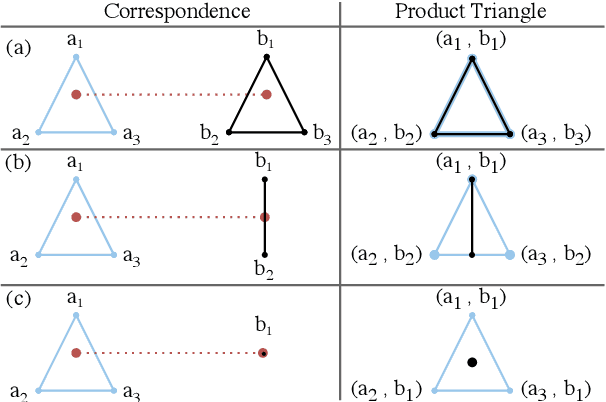
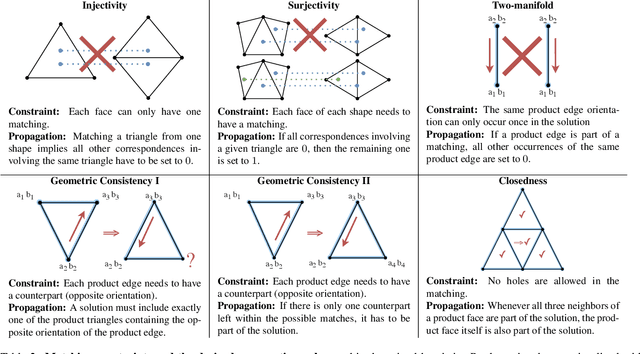
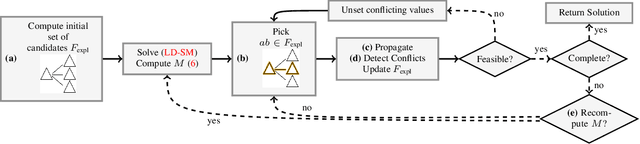
We present a scalable combinatorial algorithm for globally optimizing over the space of geometrically consistent mappings between 3D shapes. We use the mathematically elegant formalism proposed by Windheuser et al. (ICCV 2011) where 3D shape matching was formulated as an integer linear program over the space of orientation-preserving diffeomorphisms. Until now, the resulting formulation had limited practical applicability due to its complicated constraint structure and its large size. We propose a novel primal heuristic coupled with a Lagrange dual problem that is several orders of magnitudes faster compared to previous solvers. This allows us to handle shapes with substantially more triangles than previously solvable. We demonstrate compelling results on diverse datasets, and, even showcase that we can address the challenging setting of matching two partial shapes without availability of complete shapes. Our code is publicly available at http://github.com/paul0noah/sm-comb .

Structured Prediction Problem Archive

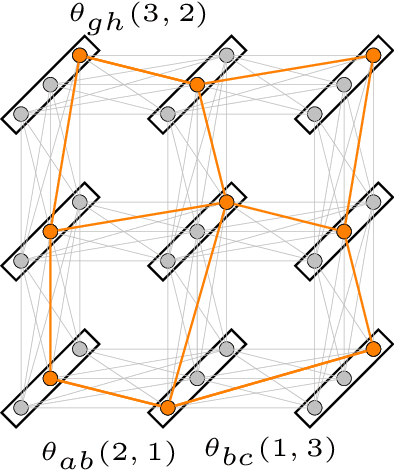
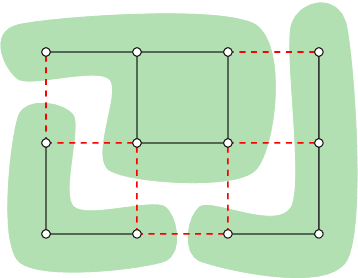
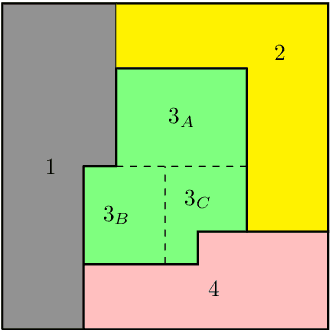
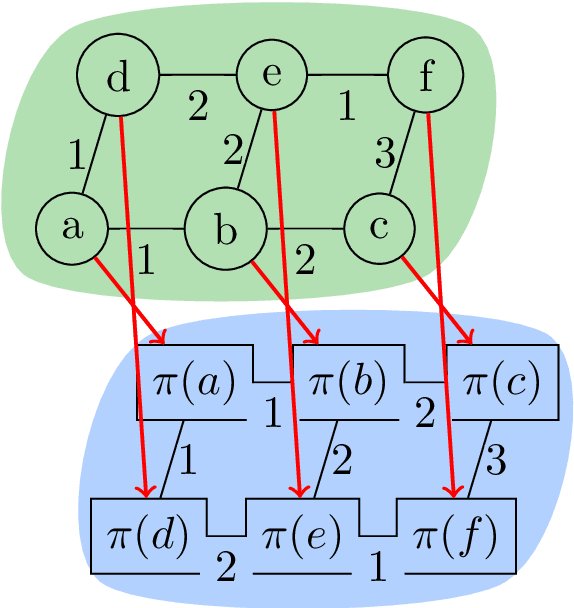
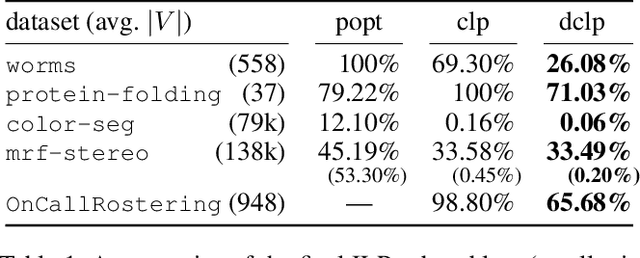
Structured prediction problems are one of the fundamental tools in machine learning. In order to facilitate algorithm development for their numerical solution, we collect in one place a large number of datasets in easy to read formats for a diverse set of problem classes. We provide archival links to datasets, description of the considered problems and problem formats, and a short summary of problem characteristics including size, number of instances etc. For reference we also give a non-exhaustive selection of algorithms proposed in the literature for their solution. We hope that this central repository will make benchmarking and comparison to established works easier. We welcome submission of interesting new datasets and algorithms for inclusion in our archive.

LMGP: Lifted Multicut Meets Geometry Projections for Multi-Camera Multi-Object Tracking

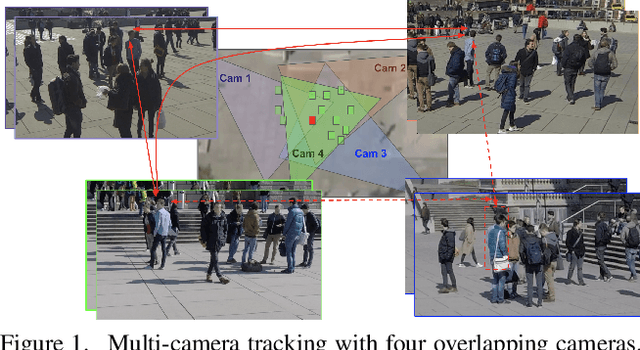
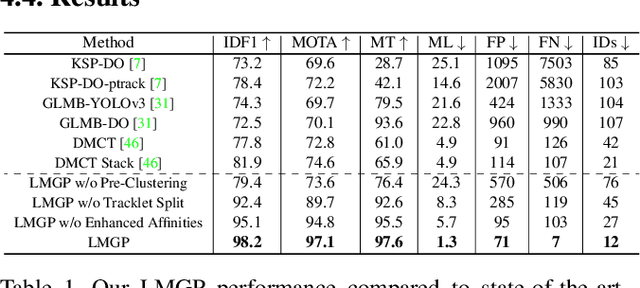
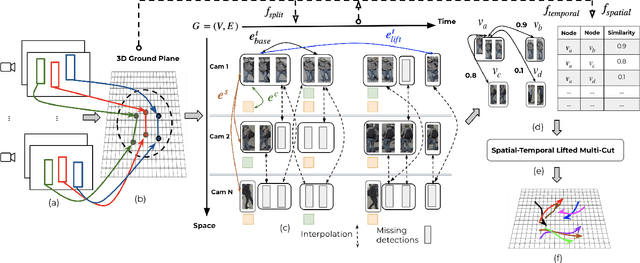
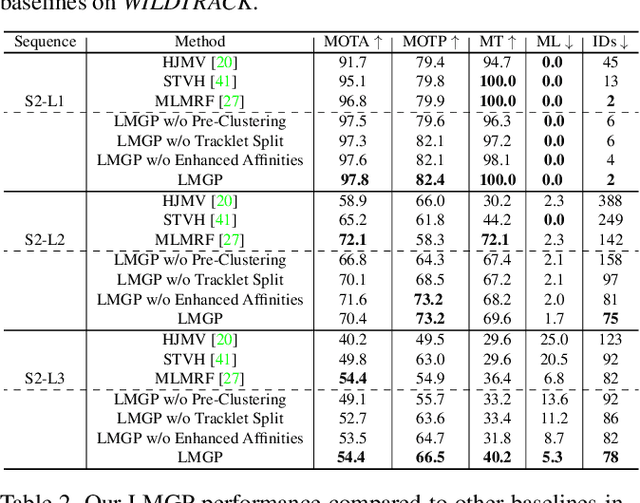
Multi-Camera Multi-Object Tracking is currently drawing attention in the computer vision field due to its superior performance in real-world applications such as video surveillance with crowded scenes or in vast space. In this work, we propose a mathematically elegant multi-camera multiple object tracking approach based on a spatial-temporal lifted multicut formulation. Our model utilizes state-of-the-art tracklets produced by single-camera trackers as proposals. As these tracklets may contain ID-Switch errors, we refine them through a novel pre-clustering obtained from 3D geometry projections. As a result, we derive a better tracking graph without ID switches and more precise affinity costs for the data association phase. Tracklets are then matched to multi-camera trajectories by solving a global lifted multicut formulation that incorporates short and long-range temporal interactions on tracklets located in the same camera as well as inter-camera ones. Experimental results on the WildTrack dataset yield near-perfect result, outperforming state-of-the-art trackers on Campus while being on par on the PETS-09 dataset. We will make our implementations available upon acceptance of the paper.

FastDOG: Fast Discrete Optimization on GPU

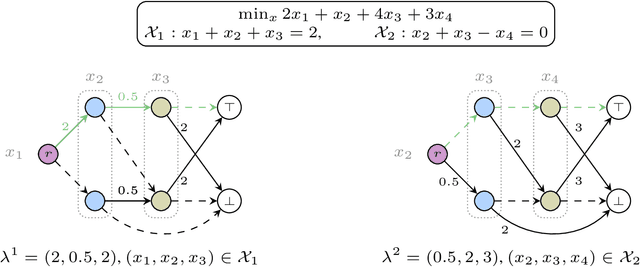
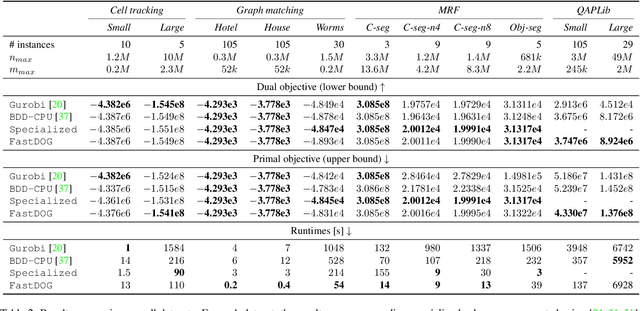
We present a massively parallel Lagrange decomposition method for solving 0-1 integer linear programs occurring in structured prediction. We propose a new iterative update scheme for solving the Lagrangean dual and a perturbation technique for decoding primal solutions. For representing subproblems we follow Lange et al. (2021) and use binary decision diagrams (BDDs). Our primal and dual algorithms require little synchronization between subproblems and optimization over BDDs needs only elementary operations without complicated control flow. This allows us to exploit the parallelism offered by GPUs for all components of our method. We present experimental results on combinatorial problems from MAP inference for Markov Random Fields, quadratic assignment and cell tracking for developmental biology. Our highly parallel GPU implementation improves upon the running times of the algorithms from Lange et al. (2021) by up to an order of magnitude. In particular, we come close to or outperform some state-of-the-art specialized heuristics while being problem agnostic.

RAMA: A Rapid Multicut Algorithm on GPU

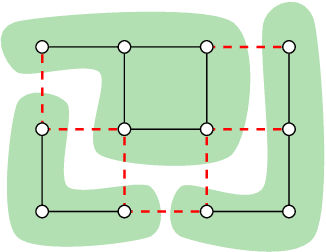
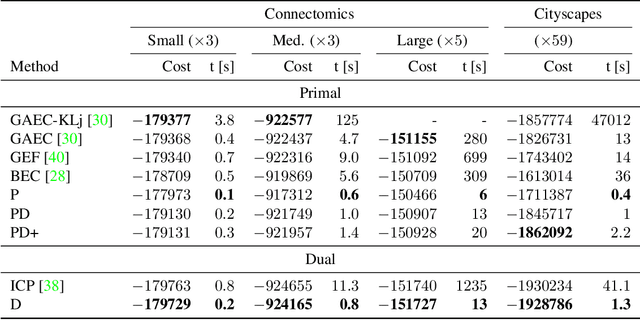
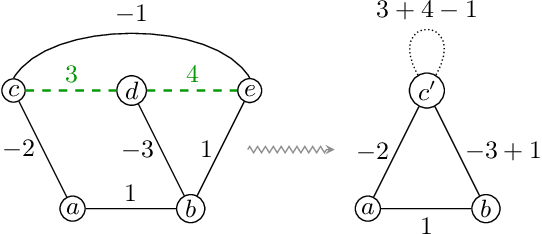
We propose a highly parallel primal-dual algorithm for the multicut (a.k.a. correlation clustering) problem, a classical graph clustering problem widely used in machine learning and computer vision. Our algorithm consists of three steps executed recursively: (1) Finding conflicted cycles that correspond to violated inequalities of the underlying multicut relaxation, (2) Performing message passing between the edges and cycles to optimize the Lagrange relaxation coming from the found violated cycles producing reduced costs and (3) Contracting edges with high reduced costs through matrix-matrix multiplications. Our algorithm produces primal solutions and dual lower bounds that estimate the distance to optimum. We implement our algorithm on GPUs and show resulting one to two order-of-magnitudes improvements in execution speed without sacrificing solution quality compared to traditional serial algorithms that run on CPUs. We can solve very large scale benchmark problems with up to $\mathcal{O}(10^8)$ variables in a few seconds with small primal-dual gaps. We make our code available at https://github.com/pawelswoboda/RAMA.

Making Higher Order MOT Scalable: An Efficient Approximate Solver for Lifted Disjoint Paths

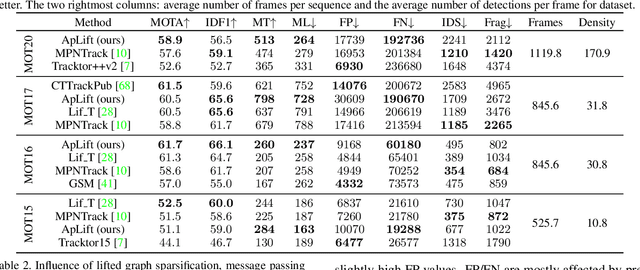
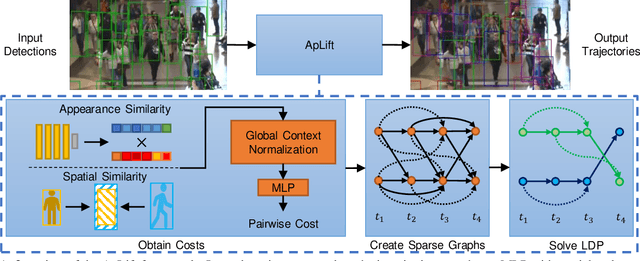
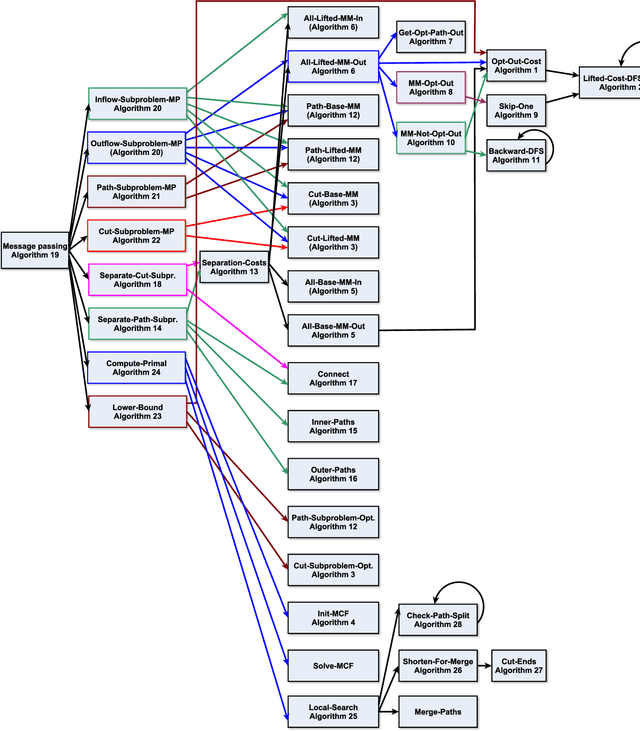
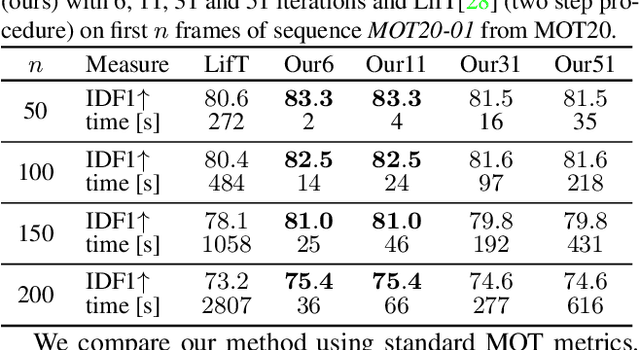
We present an efficient approximate message passing solver for the lifted disjoint paths problem (LDP), a natural but NP-hard model for multiple object tracking (MOT). Our tracker scales to very large instances that come from long and crowded MOT sequences. Our approximate solver enables us to process the MOT15/16/17 benchmarks without sacrificing solution quality and allows for solving MOT20, which has been out of reach up to now for LDP solvers due to its size and complexity. On all these four standard MOT benchmarks we achieve performance comparable or better than current state-of-the-art methods including a tracker based on an optimal LDP solver.

Combinatorial Optimization for Panoptic Segmentation: An End-to-End Trainable Approach

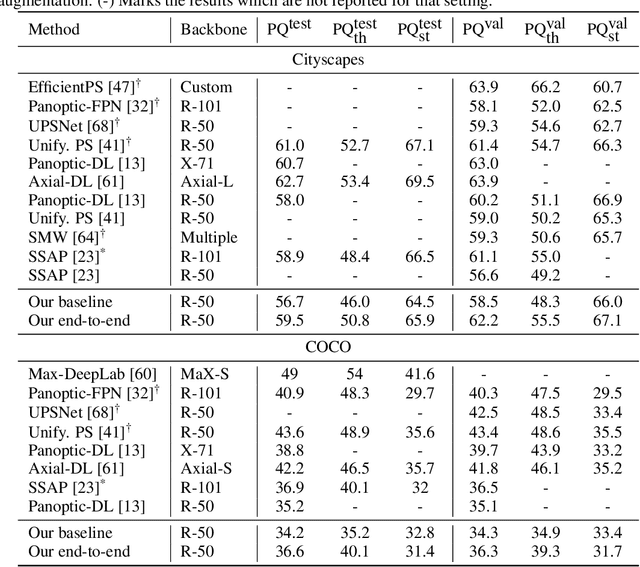
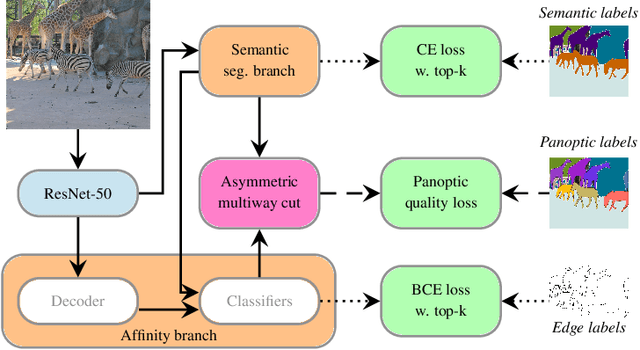
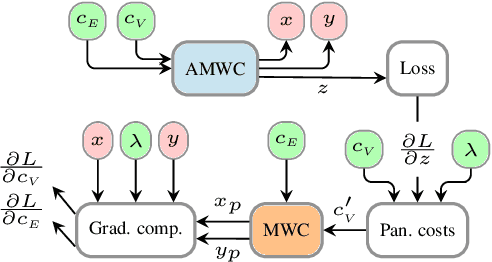
We propose an end-to-end trainable architecture for simultaneous semantic and instance segmentation (a.k.a. panoptic segmentation) consisting of a convolutional neural network and an asymmetric multiway cut problem solver. The latter solves a combinatorial optimization problem that elegantly incorporates semantic and boundary predictions to produce a panoptic labeling. Our formulation allows to directly maximize a smooth surrogate of the panoptic quality metric by backpropagating the gradient through the optimization problem. Experimental evaluation shows improvement of end-to-end learning w.r.t. comparable approaches on Cityscapes and COCO datasets. Overall, our approach shows the utility of using combinatorial optimization in tandem with deep learning in a challenging large scale real-world problem and showcases benefits and insights into training such an architecture end-to-end.

Lifted Disjoint Paths with Application in Multiple Object Tracking

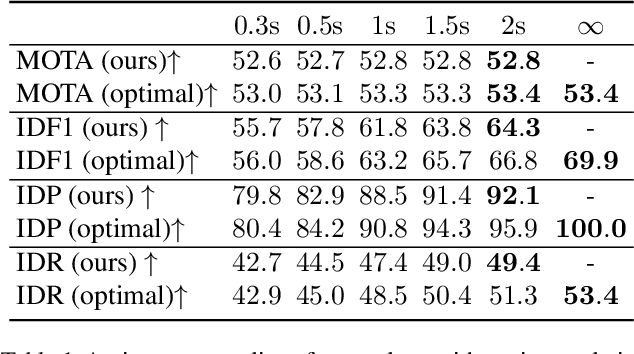
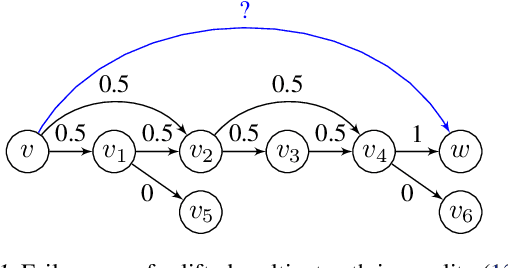
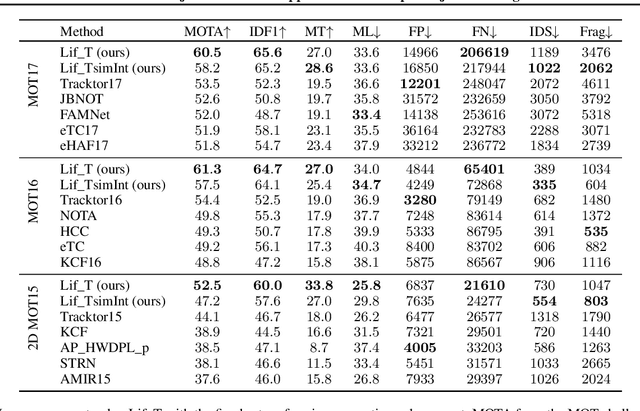
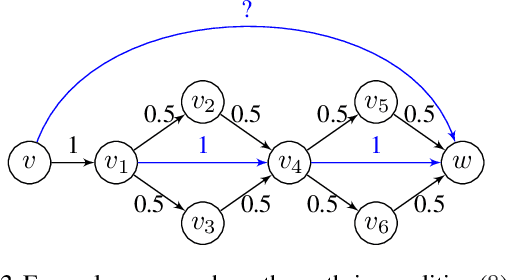
We present an extension to the disjoint paths problem in which additional \emph{lifted} edges are introduced to provide path connectivity priors. We call the resulting optimization problem the lifted disjoint paths problem. We show that this problem is NP-hard by reduction from integer multicommodity flow and 3-SAT. To enable practical global optimization, we propose several classes of linear inequalities that produce a high-quality LP-relaxation. Additionally, we propose efficient cutting plane algorithms for separating the proposed linear inequalities. The lifted disjoint path problem is a natural model for multiple object tracking and allows an elegant mathematical formulation for long range temporal interactions. Lifted edges help to prevent id switches and to re-identify persons. Our lifted disjoint paths tracker achieves nearly optimal assignments with respect to input detections. As a consequence, it leads on all three main benchmarks of the MOT challenge, improving significantly over state-of-the-art.

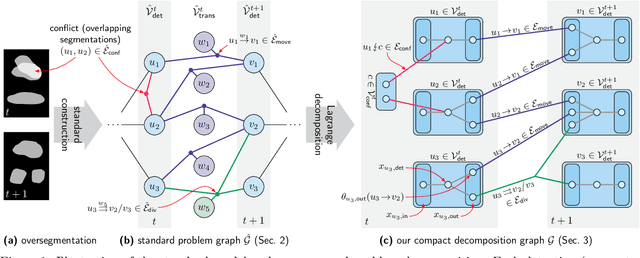
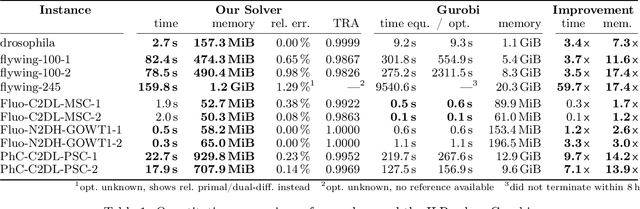
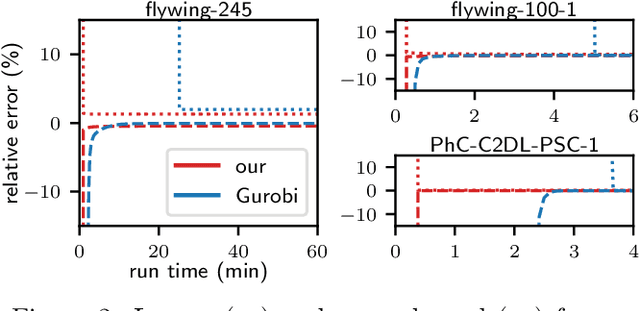
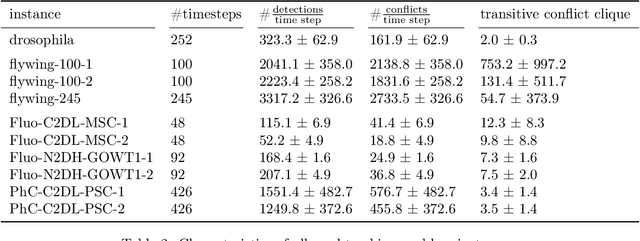
A Primal-Dual Solver for Large-Scale Tracking-by-Assignment

We propose a fast approximate solver for the combinatorial problem known as tracking-by-assignment, which we apply to cell tracking. The latter plays a key role in discovery in many life sciences, especially in cell and developmental biology. So far, in the most general setting this problem was addressed by off-the-shelf solvers like Gurobi, whose run time and memory requirements rapidly grow with the size of the input. In contrast, for our method this growth is nearly linear. Our contribution consists of a new (1) decomposable compact representation of the problem; (2) dual block-coordinate ascent method for optimizing the decomposition-based dual; and (3) primal heuristics that reconstructs a feasible integer solution based on the dual information. Compared to solving the problem with Gurobi, we observe an up to~60~times speed-up, while reducing the memory footprint significantly. We demonstrate the efficacy of our method on real-world tracking problems.

Exact MAP-Inference by Confining Combinatorial Search with LP Relaxation

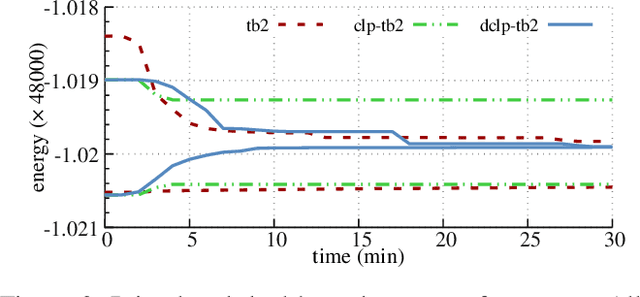
We consider the MAP-inference problem for graphical models, which is a valued constraint satisfaction problem defined on real numbers with a natural summation operation. We propose a family of relaxations (different from the famous Sherali-Adams hierarchy), which naturally define lower bounds for its optimum. This family always contains a tight relaxation and we give an algorithm able to find it and therefore, solve the initial non-relaxed NP-hard problem. The relaxations we consider decompose the original problem into two non-overlapping parts: an easy LP-tight part and a difficult one. For the latter part a combinatorial solver must be used. As we show in our experiments, in a number of applications the second, difficult part constitutes only a small fraction of the whole problem. This property allows to significantly reduce the computational time of the combinatorial solver and therefore solve problems which were out of reach before.