Role of scrambling and noise in temporal information processing with quantum systems

Scrambling quantum systems have been demonstrated as effective substrates for temporal information processing. While their role in providing rich feature maps has been widely studied, a theoretical understanding of their performance in temporal tasks is still lacking. Here we consider a general quantum reservoir processing framework that captures a broad range of physical computing models with quantum systems. We examine the scalability and memory retention of the model with scrambling reservoirs modelled by high-order unitary designs in both noiseless and noisy settings. In the former regime, we show that measurement readouts become exponentially concentrated with increasing reservoir size, yet strikingly do not worsen with the reservoir iterations. Thus, while repeatedly reusing a small scrambling reservoir with quantum data might be viable, scaling up the problem size deteriorates generalization unless one can afford an exponential shot overhead. In contrast, the memory of early inputs and initial states decays exponentially in both reservoir size and reservoir iterations. In the noisy regime, we also prove exponential memory decays with iterations for local noisy channels. Proving these results required us to introduce new proof techniques for bounding concentration in temporal quantum learning models.

A unifying account of warm start guarantees for patches of quantum landscapes

Barren plateaus are fundamentally a statement about quantum loss landscapes on average but there can, and generally will, exist patches of barren plateau landscapes with substantial gradients. Previous work has studied certain classes of parameterized quantum circuits and found example regions where gradients vanish at worst polynomially in system size. Here we present a general bound that unifies all these previous cases and that can tackle physically-motivated ans\"atze that could not be analyzed previously. Concretely, we analytically prove a lower-bound on the variance of the loss that can be used to show that in a non-exponentially narrow region around a point with curvature the loss variance cannot decay exponentially fast. This result is complemented by numerics and an upper-bound that suggest that any loss function with a barren plateau will have exponentially vanishing gradients in any constant radius subregion. Our work thus suggests that while there are hopes to be able to warm-start variational quantum algorithms, any initialization strategy that cannot get increasingly close to the region of attraction with increasing problem size is likely inadequate.

CrystalGRW: Generative Modeling of Crystal Structures with Targeted Properties via Geodesic Random Walks

Determining whether a candidate crystalline material is thermodynamically stable depends on identifying its true ground-state structure, a central challenge in computational materials science. We introduce CrystalGRW, a diffusion-based generative model on Riemannian manifolds that proposes novel crystal configurations and can predict stable phases validated by density functional theory. The crystal properties, such as fractional coordinates, atomic types, and lattice matrices, are represented on suitable Riemannian manifolds, ensuring that new predictions generated through the diffusion process preserve the periodicity of crystal structures. We incorporate an equivariant graph neural network to also account for rotational and translational symmetries during the generation process. CrystalGRW demonstrates the ability to generate realistic crystal structures that are close to their ground states with accuracy comparable to existing models, while also enabling conditional control, such as specifying a desired crystallographic point group. These features help accelerate materials discovery and inverse design by offering stable, symmetry-consistent crystal candidates for experimental validation.

Dissipation alters modes of information encoding in small quantum reservoirs near criticality

Quantum reservoir computing (QRC) has emerged as a promising paradigm for harnessing near-term quantum devices to tackle temporal machine learning tasks. Yet identifying the mechanisms that underlie enhanced performance remains challenging, particularly in many-body open systems where nonlinear interactions and dissipation intertwine in complex ways. Here, we investigate a minimal model of a driven-dissipative quantum reservoir described by two coupled Kerr-nonlinear oscillators, an experimentally realizable platform that features controllable coupling, intrinsic nonlinearity, and tunable photon loss. Using Partial Information Decomposition (PID), we examine how different dynamical regimes encode input drive signals in terms of redundancy (information shared by each oscillator) and synergy (information accessible only through their joint observation). Our key results show that, near a critical point marking a dynamical bifurcation, the system transitions from predominantly redundant to synergistic encoding. We further demonstrate that synergy amplifies short-term responsiveness, thereby enhancing immediate memory retention, whereas strong dissipation leads to more redundant encoding that supports long-term memory retention. These findings elucidate how the interplay of instability and dissipation shapes information processing in small quantum systems, providing a fine-grained, information-theoretic perspective for analyzing and designing QRC platforms.

On fundamental aspects of quantum extreme learning machines

Quantum Extreme Learning Machines (QELMs) have emerged as a promising framework for quantum machine learning. Their appeal lies in the rich feature map induced by the dynamics of a quantum substrate - the quantum reservoir - and the efficient post-measurement training via linear regression. Here we study the expressivity of QELMs by decomposing the prediction of QELMs into a Fourier series. We show that the achievable Fourier frequencies are determined by the data encoding scheme, while Fourier coefficients depend on both the reservoir and the measurement. Notably, the expressivity of QELMs is fundamentally limited by the number of Fourier frequencies and the number of observables, while the complexity of the prediction hinges on the reservoir. As a cautionary note on scalability, we identify four sources that can lead to the exponential concentration of the observables as the system size grows (randomness, hardware noise, entanglement, and global measurements) and show how this can turn QELMs into useless input-agnostic oracles. Our analysis elucidates the potential and fundamental limitations of QELMs, and lays the groundwork for systematically exploring quantum reservoir systems for other machine learning tasks.

Quantum Next Generation Reservoir Computing: An Efficient Quantum Algorithm for Forecasting Quantum Dynamics

Next Generation Reservoir Computing (NG-RC) is a modern class of model-free machine learning that enables an accurate forecasting of time series data generated by dynamical systems. We demonstrate that NG-RC can accurately predict full many-body quantum dynamics, instead of merely concentrating on the dynamics of observables, which is the conventional application of reservoir computing. In addition, we apply a technique which we refer to as skipping ahead to predict far future states accurately without the need to extract information about the intermediate states. However, adopting a classical NG-RC for many-body quantum dynamics prediction is computationally prohibitive due to the large Hilbert space of sample input data. In this work, we propose an end-to-end quantum algorithm for many-body quantum dynamics forecasting with a quantum computational speedup via the block-encoding technique. This proposal presents an efficient model-free quantum scheme to forecast quantum dynamics coherently, bypassing inductive biases incurred in a model-based approach.

Diffusion probabilistic models enhance variational autoencoder for crystal structure generative modeling

The crystal diffusion variational autoencoder (CDVAE) is a machine learning model that leverages score matching to generate realistic crystal structures that preserve crystal symmetry. In this study, we leverage novel diffusion probabilistic (DP) models to denoise atomic coordinates rather than adopting the standard score matching approach in CDVAE. Our proposed DP-CDVAE model can reconstruct and generate crystal structures whose qualities are statistically comparable to those of the original CDVAE. Furthermore, notably, when comparing the carbon structures generated by the DP-CDVAE model with relaxed structures obtained from density functional theory calculations, we find that the DP-CDVAE generated structures are remarkably closer to their respective ground states. The energy differences between these structures and the true ground states are, on average, 68.1 meV/atom lower than those generated by the original CDVAE. This significant improvement in the energy accuracy highlights the effectiveness of the DP-CDVAE model in generating crystal structures that better represent their ground-state configurations.

StrainNet: Predicting crystal structure elastic properties using SE(3)-equivariant graph neural networks

Accurately predicting the elastic properties of crystalline solids is vital for computational materials science. However, traditional atomistic scale ab initio approaches are computationally intensive, especially for studying complex materials with a large number of atoms in a unit cell. We introduce a novel data-driven approach to efficiently predict the elastic properties of crystal structures using SE(3)-equivariant graph neural networks (GNNs). This approach yields important scalar elastic moduli with the accuracy comparable to recent data-driven studies. Importantly, our symmetry-aware GNNs model also enables the prediction of the strain energy density (SED) and the associated elastic constants, the fundamental tensorial quantities that are significantly influenced by a material's crystallographic group. The model consistently distinguishes independent elements of SED tensors, in accordance with the symmetry of the crystal structures. Finally, our deep learning model possesses meaningful latent features, offering an interpretable prediction of the elastic properties.

Explainable Natural Language Processing with Matrix Product States

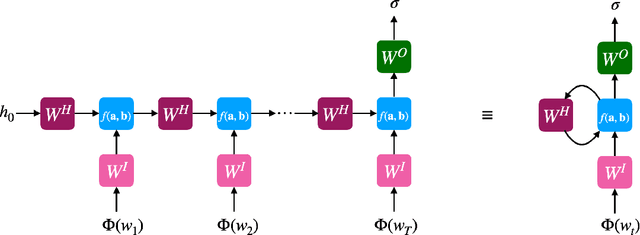
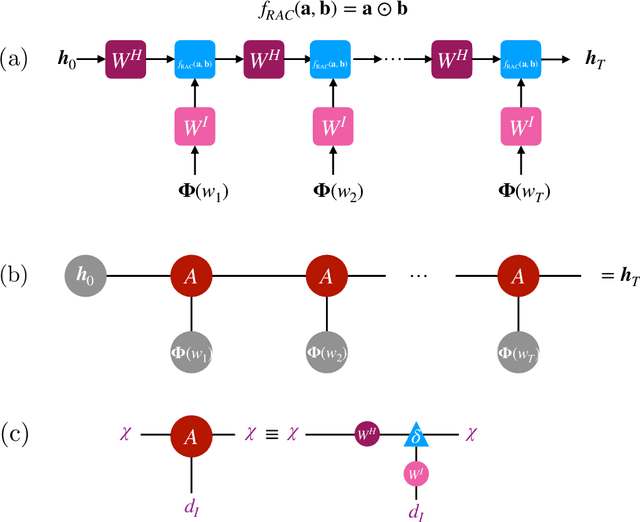
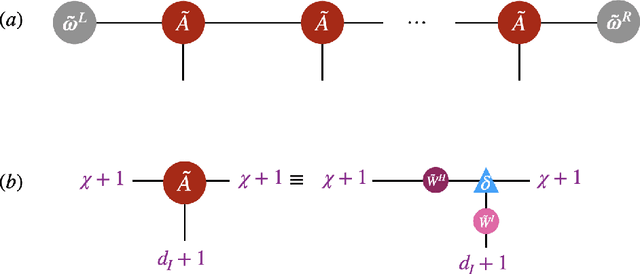
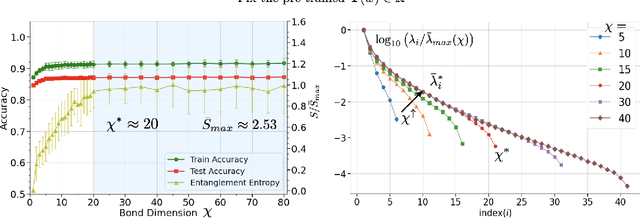
Despite empirical successes of recurrent neural networks (RNNs) in natural language processing (NLP), theoretical understanding of RNNs is still limited due to intrinsically complex computations in RNNs. We perform a systematic analysis of RNNs' behaviors in a ubiquitous NLP task, the sentiment analysis of movie reviews, via the mapping between a class of RNNs called recurrent arithmetic circuits (RACs) and a matrix product state (MPS). Using the von-Neumann entanglement entropy (EE) as a proxy for information propagation, we show that single-layer RACs possess a maximum information propagation capacity, reflected by the saturation of the EE. Enlarging the bond dimension of an MPS beyond the EE saturation threshold does not increase the prediction accuracies, so a minimal model that best estimates the data statistics can be constructed. Although the saturated EE is smaller than the maximum EE achievable by the area law of an MPS, our model achieves ~99% training accuracies in realistic sentiment analysis data sets. Thus, low EE alone is not a warrant against the adoption of single-layer RACs for NLP. Contrary to a common belief that long-range information propagation is the main source of RNNs' expressiveness, we show that single-layer RACs also harness high expressiveness from meaningful word vector embeddings. Our work sheds light on the phenomenology of learning in RACs and more generally on the explainability aspects of RNNs for NLP, using tools from many-body quantum physics.

Quantum diffusion map for nonlinear dimensionality reduction

Inspired by random walk on graphs, diffusion map (DM) is a class of unsupervised machine learning that offers automatic identification of low-dimensional data structure hidden in a high-dimensional dataset. In recent years, among its many applications, DM has been successfully applied to discover relevant order parameters in many-body systems, enabling automatic classification of quantum phases of matter. However, classical DM algorithm is computationally prohibitive for a large dataset, and any reduction of the time complexity would be desirable. With a quantum computational speedup in mind, we propose a quantum algorithm for DM, termed quantum diffusion map (qDM). Our qDM takes as an input N classical data vectors, performs an eigen-decomposition of the Markov transition matrix in time $O(\log^3 N)$, and classically constructs the diffusion map via the readout (tomography) of the eigenvectors, giving a total runtime of $O(N^2 \text{polylog}\, N)$. Lastly, quantum subroutines in qDM for constructing a Markov transition operator, and for analyzing its spectral properties can also be useful for other random walk-based algorithms.