Robust Moment Identification for Nonlinear PDEs via a Neural ODE Approach

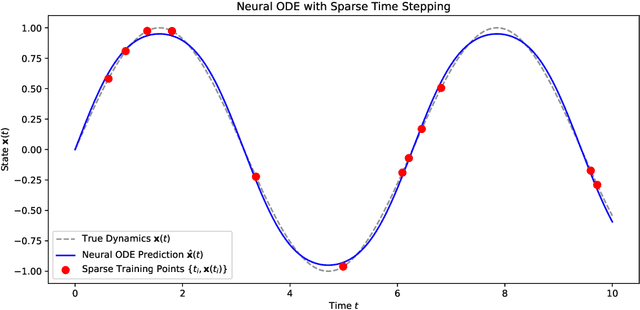
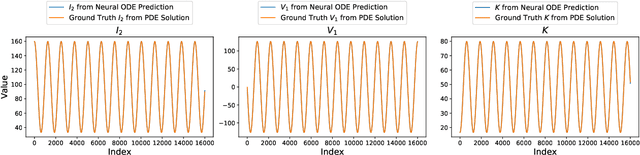
We propose a data-driven framework for learning reduced-order moment dynamics from PDE-governed systems using Neural ODEs. In contrast to derivative-based methods like SINDy, which necessitate densely sampled data and are sensitive to noise, our approach based on Neural ODEs directly models moment trajectories, enabling robust learning from sparse and potentially irregular time series. Using as an application platform the nonlinear Schr\"{o}dinger equation, the framework accurately recovers governing moment dynamics when closure is available, even with limited and irregular observations. For systems without analytical closure, we introduce a data-driven coordinate transformation strategy based on Stiefel manifold optimization, enabling the discovery of low-dimensional representations in which the moment dynamics become closed, facilitating interpretable and reliable modeling. We also explore cases where a closure model is not known, such as a Fisher-KPP reaction-diffusion system. Here we demonstrate that Neural ODEs can still effectively approximate the unclosed moment dynamics and achieve superior extrapolation accuracy compared to physical-expert-derived ODE models. This advantage remains robust even under sparse and irregular sampling, highlighting the method's robustness in data-limited settings. Our results highlight the Neural ODE framework as a powerful and flexible tool for learning interpretable, low-dimensional moment dynamics in complex PDE-governed systems.

Data-Driven Discovery of Conservation Laws from Trajectories via Neural Deflation

In an earlier work by a subset of the present authors, the method of the so-called neural deflation was introduced towards identifying a complete set of functionally independent conservation laws of a nonlinear dynamical system. Here, we extend by a significant step this proposal. Instead of using the explicit knowledge of the underlying equations of motion, we develop the method directly from system trajectories. This is crucial towards enhancing the practical implementation of the method in scenarios where solely data reflecting discrete snapshots of the system are available. We showcase the results of the method and the number of associated conservation laws obtained in a diverse range of examples including 1D and 2D harmonic oscillators, the Toda lattice, the Fermi-Pasta-Ulam-Tsingou lattice and the Calogero-Moser system.

A Modified PINN Approach for Identifiable Compartmental Models in Epidemiology with Applications to COVID-19

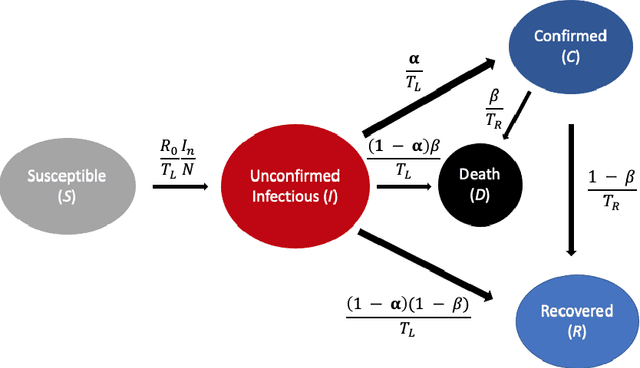
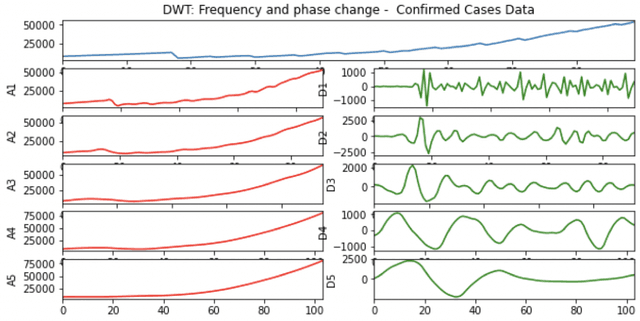
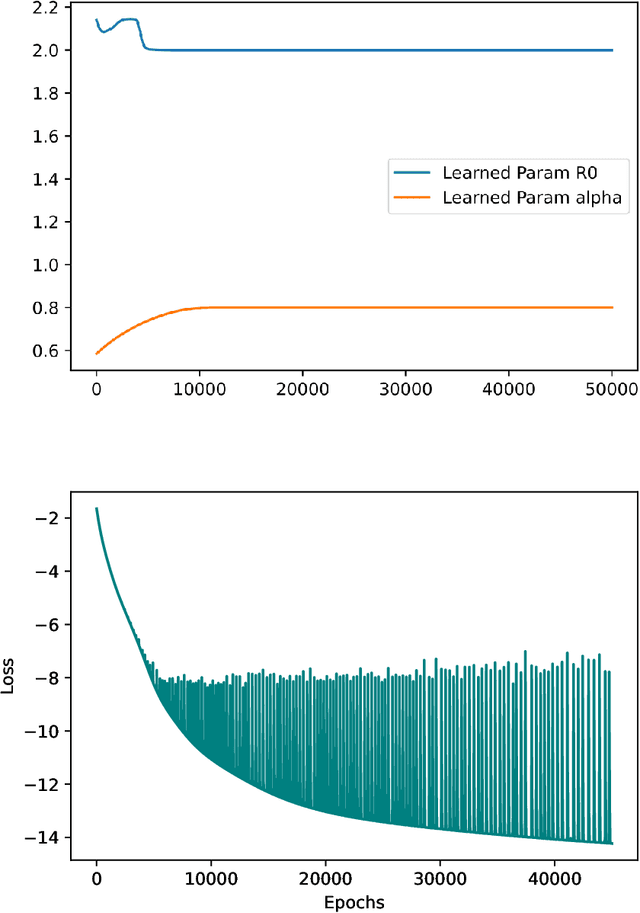
A variety of approaches using compartmental models have been used to study the COVID-19 pandemic and the usage of machine learning methods with these models has had particularly notable success. We present here an approach toward analyzing accessible data on Covid-19's U.S. development using a variation of the "Physics Informed Neural Networks" (PINN) which is capable of using the knowledge of the model to aid learning. We illustrate the challenges of using the standard PINN approach, then how with appropriate and novel modifications to the loss function the network can perform well even in our case of incomplete information. Aspects of identifiability of the model parameters are also assessed, as well as methods of denoising available data using a wavelet transform. Finally, we discuss the capability of the neural network methodology to work with models of varying parameter values, as well as a concrete application in estimating how effectively cases are being tested for in a population, providing a ranking of U.S. states by means of their respective testing.