Ranking by Lifts: A Cost-Benefit Approach to Large-Scale A/B Tests

A/B testers conducting large-scale tests prioritize lifts and want to be able to control false rejections of the null. This work develops a decision-theoretic framework for maximizing profits subject to false discovery rate (FDR) control. We build an empirical Bayes solution for the problem via the greedy knapsack approach. We derive an oracle rule based on ranking the ratio of expected lifts and the cost of wrong rejections using the local false discovery rate (lfdr) statistic. Our oracle decision rule is valid and optimal for large-scale tests. Further, we establish asymptotic validity for the data-driven procedure and demonstrate finite-sample validity in experimental studies. We also demonstrate the merit of the proposed method over other FDR control methods. Finally, we discuss an application to actual Optimizely experiments.

Large-Scale Model Selection with Misspecification

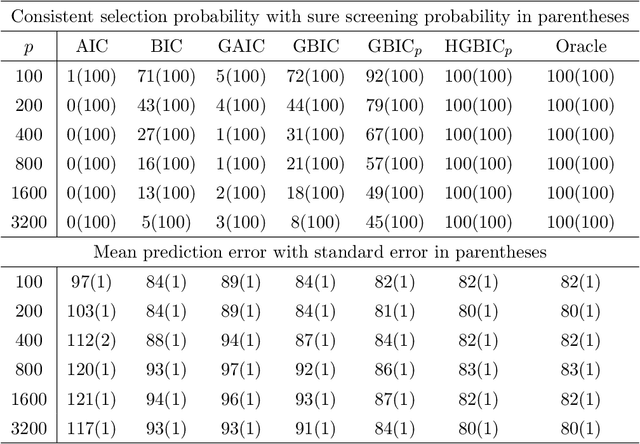
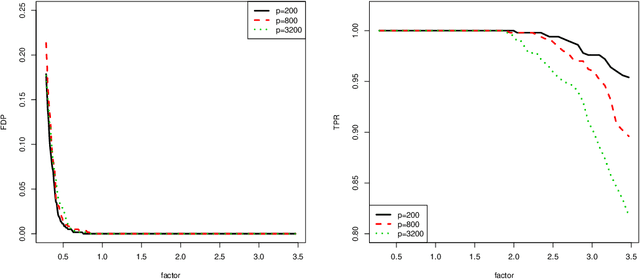
Model selection is crucial to high-dimensional learning and inference for contemporary big data applications in pinpointing the best set of covariates among a sequence of candidate interpretable models. Most existing work assumes implicitly that the models are correctly specified or have fixed dimensionality. Yet both features of model misspecification and high dimensionality are prevalent in practice. In this paper, we exploit the framework of model selection principles in misspecified models originated in Lv and Liu (2014) and investigate the asymptotic expansion of Bayesian principle of model selection in the setting of high-dimensional misspecified models. With a natural choice of prior probabilities that encourages interpretability and incorporates Kullback-Leibler divergence, we suggest the high-dimensional generalized Bayesian information criterion with prior probability (HGBIC_p) for large-scale model selection with misspecification. Our new information criterion characterizes the impacts of both model misspecification and high dimensionality on model selection. We further establish the consistency of covariance contrast matrix estimation and the model selection consistency of HGBIC_p in ultra-high dimensions under some mild regularity conditions. The advantages of our new method are supported by numerical studies.

Model Selection in High-Dimensional Misspecified Models

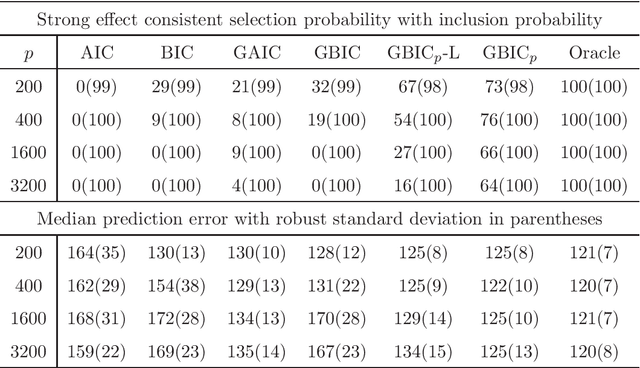
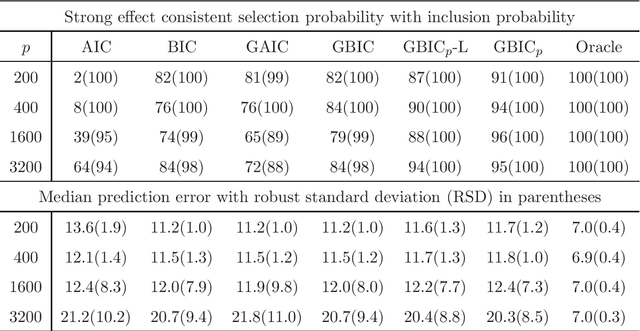
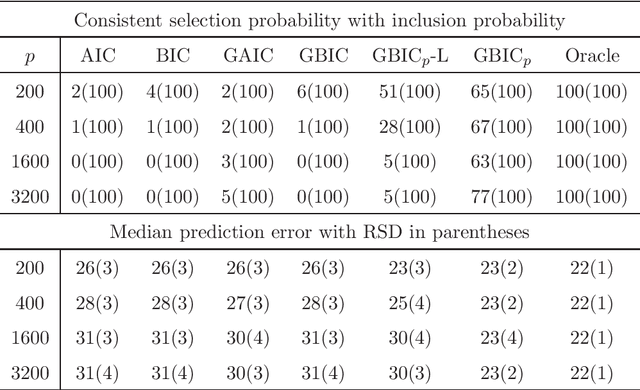
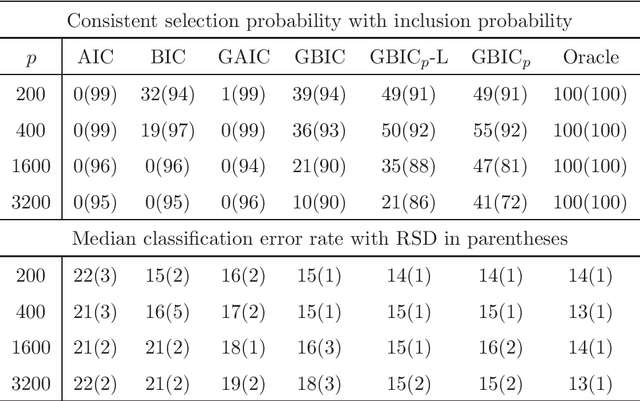
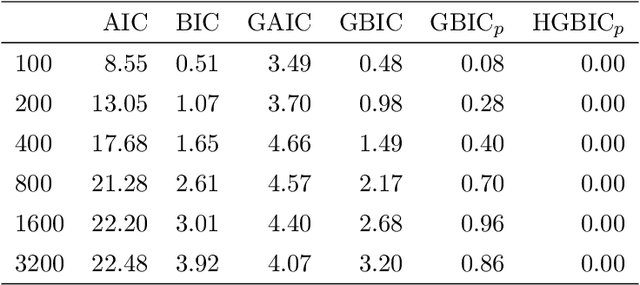
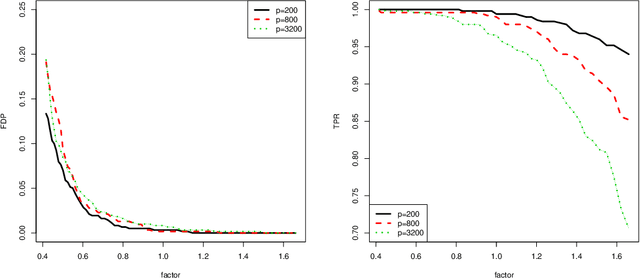
Model selection is indispensable to high-dimensional sparse modeling in selecting the best set of covariates among a sequence of candidate models. Most existing work assumes implicitly that the model is correctly specified or of fixed dimensions. Yet model misspecification and high dimensionality are common in real applications. In this paper, we investigate two classical Kullback-Leibler divergence and Bayesian principles of model selection in the setting of high-dimensional misspecified models. Asymptotic expansions of these principles reveal that the effect of model misspecification is crucial and should be taken into account, leading to the generalized AIC and generalized BIC in high dimensions. With a natural choice of prior probabilities, we suggest the generalized BIC with prior probability which involves a logarithmic factor of the dimensionality in penalizing model complexity. We further establish the consistency of the covariance contrast matrix estimator in a general setting. Our results and new method are supported by numerical studies.