No-Regret Online Prediction with Strategic Experts

We study a generalization of the online binary prediction with expert advice framework where at each round, the learner is allowed to pick $m\geq 1$ experts from a pool of $K$ experts and the overall utility is a modular or submodular function of the chosen experts. We focus on the setting in which experts act strategically and aim to maximize their influence on the algorithm's predictions by potentially misreporting their beliefs about the events. Among others, this setting finds applications in forecasting competitions where the learner seeks not only to make predictions by aggregating different forecasters but also to rank them according to their relative performance. Our goal is to design algorithms that satisfy the following two requirements: 1) $\textit{Incentive-compatible}$: Incentivize the experts to report their beliefs truthfully, and 2) $\textit{No-regret}$: Achieve sublinear regret with respect to the true beliefs of the best fixed set of $m$ experts in hindsight. Prior works have studied this framework when $m=1$ and provided incentive-compatible no-regret algorithms for the problem. We first show that a simple reduction of our problem to the $m=1$ setting is neither efficient nor effective. Then, we provide algorithms that utilize the specific structure of the utility functions to achieve the two desired goals.

Interactive Combinatorial Bandits: Balancing Competitivity and Complementarity

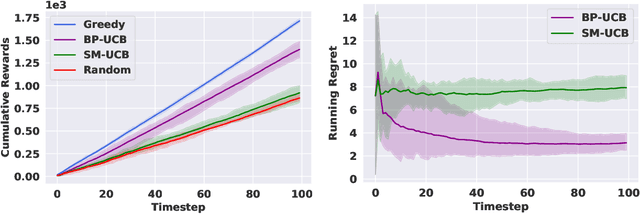
We study non-modular function maximization in the online interactive bandit setting. We are motivated by applications where there is a natural complementarity between certain elements: e.g., in a movie recommendation system, watching the first movie in a series complements the experience of watching a second (and a third, etc.). This is not expressible using only submodular functions which can represent only competitiveness between elements. We extend the purely submodular approach in two ways. First, we assume that the objective can be decomposed into the sum of monotone suBmodular and suPermodular function, known as a BP objective. Here, complementarity is naturally modeled by the supermodular component. We develop a UCB-style algorithm, where at each round a noisy gain is revealed after an action is taken that balances refining beliefs about the unknown objectives (exploration) and choosing actions that appear promising (exploitation). Defining regret in terms of submodular and supermodular curvature with respect to a full-knowledge greedy baseline, we show that this algorithm achieves at most $O(\sqrt{T})$ regret after $T$ rounds of play. Second, for those functions that do not admit a BP structure, we provide analogous regret guarantees in terms of their submodularity ratio; this is applicable for functions that are almost, but not quite, submodular. We numerically study the tasks of movie recommendation on the MovieLens dataset, and selection of training subsets for classification. Through these examples, we demonstrate the algorithm's performance as well as the shortcomings of viewing these problems as being solely submodular.

Faster First-Order Algorithms for Monotone Strongly DR-Submodular Maximization

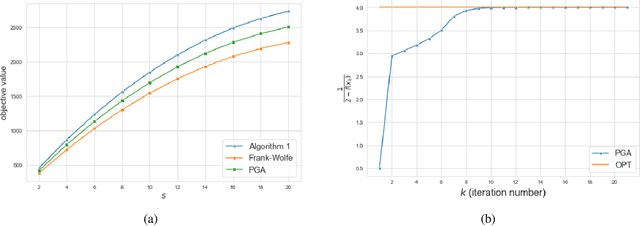
Continuous DR-submodular functions are a class of generally non-convex/non-concave functions that satisfy the Diminishing Returns (DR) property, which implies that they are concave along non-negative directions. Existing work has studied monotone continuous DR-submodular maximization subject to a convex constraint and provided efficient algorithms with approximation guarantees. In many applications, such as computing the stability number of a graph, the monotone DR-submodular objective function has the additional property of being strongly concave along non-negative directions (i.e., strongly DR-submodular). In this paper, we consider a subclass of $L$-smooth monotone DR-submodular functions that are strongly DR-submodular and have a bounded curvature, and we show how to exploit such additional structure to obtain faster algorithms with stronger guarantees for the maximization problem. We propose a new algorithm that matches the provably optimal $1-\frac{c}{e}$ approximation ratio after only $\lceil\frac{L}{\mu}\rceil$ iterations, where $c\in[0,1]$ and $\mu\geq 0$ are the curvature and the strong DR-submodularity parameter. Furthermore, we study the Projected Gradient Ascent (PGA) method for this problem, and provide a refined analysis of the algorithm with an improved $\frac{1}{1+c}$ approximation ratio (compared to $\frac{1}{2}$ in prior works) and a linear convergence rate. Experimental results illustrate and validate the efficiency and effectiveness of our proposed algorithms.

Improved Regret Bounds for Online Submodular Maximization

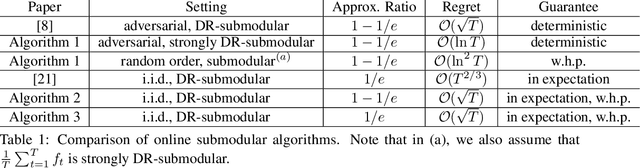
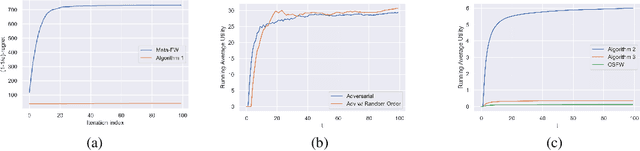
In this paper, we consider an online optimization problem over $T$ rounds where at each step $t\in[T]$, the algorithm chooses an action $x_t$ from the fixed convex and compact domain set $\mathcal{K}$. A utility function $f_t(\cdot)$ is then revealed and the algorithm receives the payoff $f_t(x_t)$. This problem has been previously studied under the assumption that the utilities are adversarially chosen monotone DR-submodular functions and $\mathcal{O}(\sqrt{T})$ regret bounds have been derived. We first characterize the class of strongly DR-submodular functions and then, we derive regret bounds for the following new online settings: $(1)$ $\{f_t\}_{t=1}^T$ are monotone strongly DR-submodular and chosen adversarially, $(2)$ $\{f_t\}_{t=1}^T$ are monotone submodular (while the average $\frac{1}{T}\sum_{t=1}^T f_t$ is strongly DR-submodular) and chosen by an adversary but they arrive in a uniformly random order, $(3)$ $\{f_t\}_{t=1}^T$ are drawn i.i.d. from some unknown distribution $f_t\sim \mathcal{D}$ where the expected function $f(\cdot)=\mathbb{E}_{f_t\sim\mathcal{D}}[f_t(\cdot)]$ is monotone DR-submodular. For $(1)$, we obtain the first logarithmic regret bounds. In terms of the second framework, we show that it is possible to obtain similar logarithmic bounds with high probability. Finally, for the i.i.d. model, we provide algorithms with $\tilde{\mathcal{O}}(\sqrt{T})$ stochastic regret bound, both in expectation and with high probability. Experimental results demonstrate that our algorithms outperform the previous techniques in the aforementioned three settings.

Function Design for Improved Competitive Ratio in Online Resource Allocation with Procurement Costs

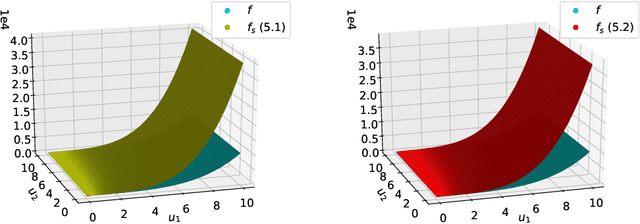
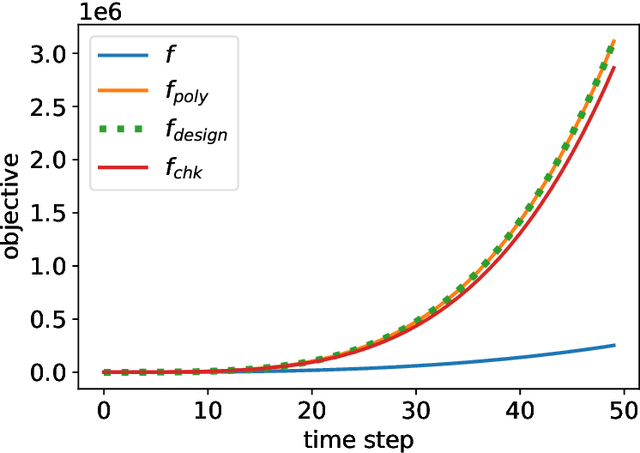
We study the problem of online resource allocation, where multiple customers arrive sequentially and the seller must irrevocably allocate resources to each incoming customer while also facing a procurement cost for the total allocation. Assuming resource procurement follows an a priori known marginally increasing cost function, the objective is to maximize the reward obtained from fulfilling the customers' requests sans the cumulative procurement cost. We analyze the competitive ratio of a primal-dual algorithm in this setting, and develop an optimization framework for synthesizing a surrogate function for the procurement cost function to be used by the algorithm, in order to improve the competitive ratio of the primal-dual algorithm. Our first design method focuses on polynomial procurement cost functions and uses the optimal surrogate function to provide a more refined bound than the state of the art. Our second design method uses quasiconvex optimization to find optimal design parameters for a general class of procurement cost functions. Numerical examples are used to illustrate the design techniques. We conclude by extending the analysis to devise a posted pricing mechanism in which the algorithm does not require the customers' preferences to be revealed.

Online DR-Submodular Maximization with Stochastic Cumulative Constraints

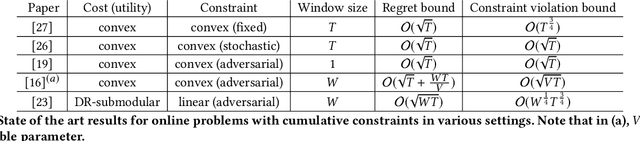
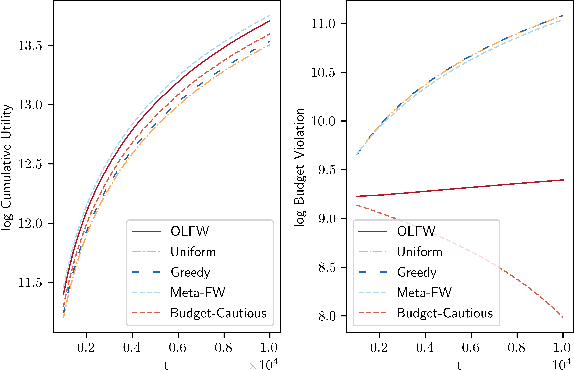
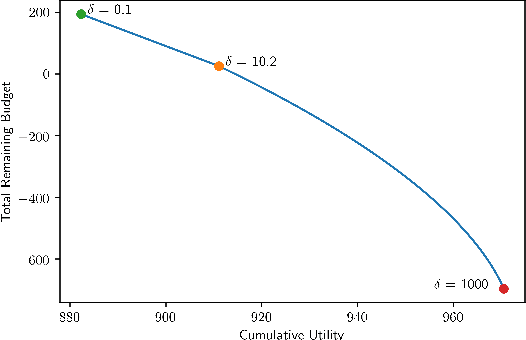
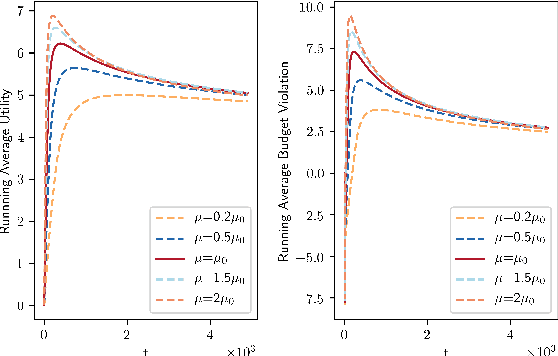
In this paper, we consider online continuous DR-submodular maximization with linear stochastic long-term constraints. Compared to the prior work on online submodular maximization, our setting introduces the extra complication of stochastic linear constraint functions that are i.i.d. generated at each round. To be precise, at step $t\in\{1,\dots,T\}$, a DR-submodular utility function $f_t(\cdot)$ and a constraint vector $p_t$, i.i.d. generated from an unknown distribution with mean $p$, are revealed after committing to an action $x_t$ and we aim to maximize the overall utility while the expected cumulative resource consumption $\sum_{t=1}^T \langle p,x_t\rangle$ is below a fixed budget $B_T$. Stochastic long-term constraints arise naturally in applications where there is a limited budget or resource available and resource consumption at each step is governed by stochastically time-varying environments. We propose the Online Lagrangian Frank-Wolfe (OLFW) algorithm to solve this class of online problems. We analyze the performance of the OLFW algorithm and we obtain sub-linear regret bounds as well as sub-linear cumulative constraint violation bounds, both in expectation and with high probability.

Online Continuous DR-Submodular Maximization with Long-Term Budget Constraints

In this paper, we study a class of online optimization problems with long-term budget constraints where the objective functions are not necessarily concave (nor convex) but they instead satisfy the Diminishing Returns (DR) property. Specifically, a sequence of monotone DR-submodular objective functions $\{f_t(x)\}_{t=1}^T$ and monotone linear budget functions $\{\langle p_t,x \rangle \}_{t=1}^T$ arrive over time and assuming a total targeted budget $B_T$, the goal is to choose points $x_t$ at each time $t\in\{1,\dots,T\}$, without knowing $f_t$ and $p_t$ on that step, to achieve sub-linear regret bound while the total budget violation $\sum_{t=1}^T \langle p_t,x_t \rangle -B_T$ is sub-linear as well. Prior work has shown that achieving sub-linear regret is impossible if the budget functions are chosen adversarially. Therefore, we modify the notion of regret by comparing the agent against a $(1-\frac{1}{e})$-approximation to the best fixed decision in hindsight which satisfies the budget constraint proportionally over any window of length $W$. We propose the Online Saddle Point Hybrid Gradient (OSPHG) algorithm to solve this class of online problems. For $W=T$, we recover the aforementioned impossibility result. However, when $W=o(T)$, we show that it is possible to obtain sub-linear bounds for both the $(1-\frac{1}{e})$-regret and the total budget violation.

Competitive Algorithms for Online Budget-Constrained Continuous DR-Submodular Problems

In this paper, we study a certain class of online optimization problems, where the goal is to maximize a function that is not necessarily concave and satisfies the Diminishing Returns (DR) property under budget constraints. We analyze a primal-dual algorithm, called the Generalized Sequential algorithm, and we obtain the first bound on the competitive ratio of online monotone DR-submodular function maximization subject to linear packing constraints which matches the known tight bound in the special case of linear objective function.