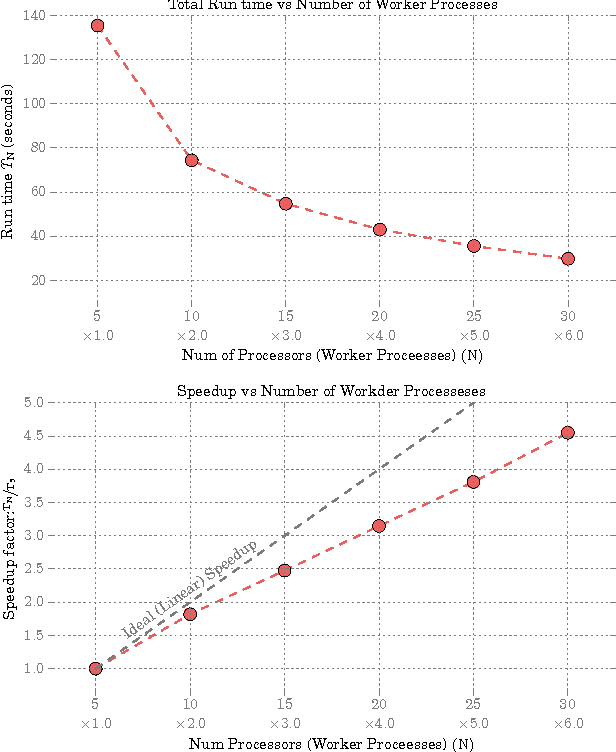
Generalized Byzantine-tolerant SGD

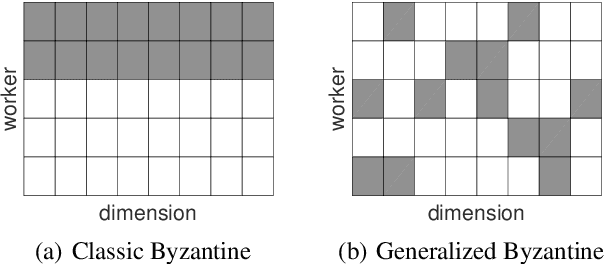
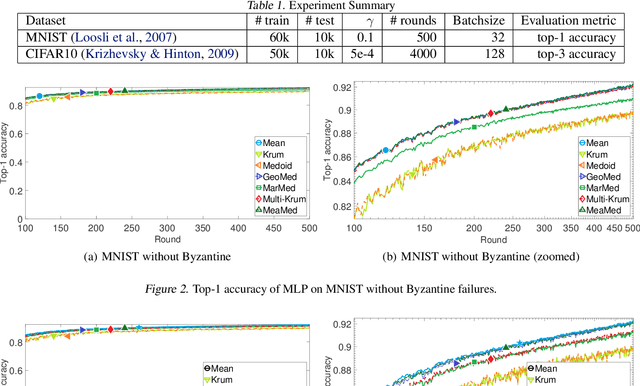
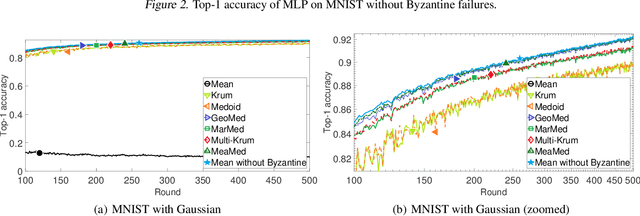
We propose three new robust aggregation rules for distributed synchronous Stochastic Gradient Descent~(SGD) under a general Byzantine failure model. The attackers can arbitrarily manipulate the data transferred between the servers and the workers in the parameter server~(PS) architecture. We prove the Byzantine resilience properties of these aggregation rules. Empirical analysis shows that the proposed techniques outperform current approaches for realistic use cases and Byzantine attack scenarios.

Learning the Base Distribution in Implicit Generative Models

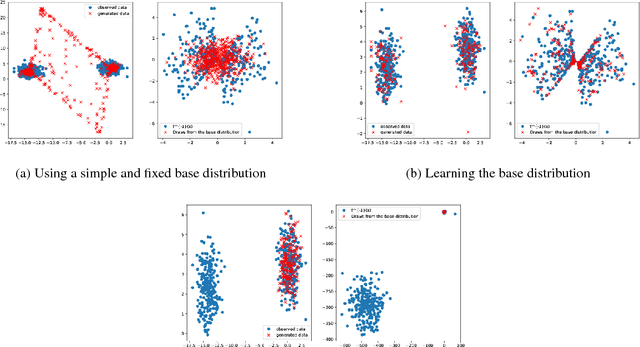
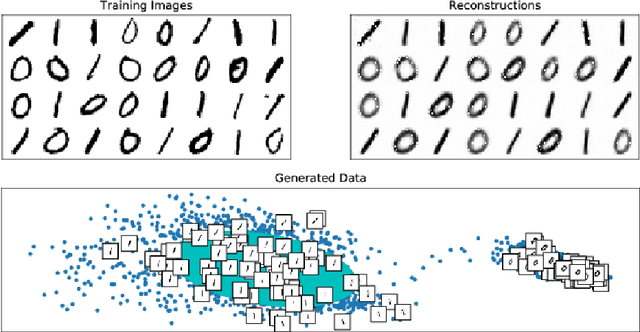
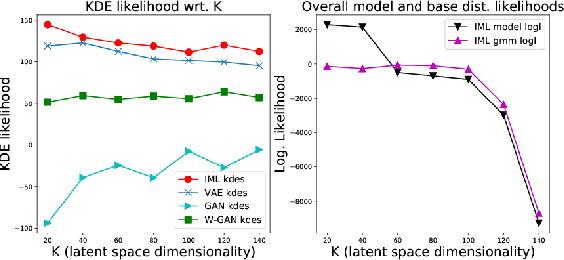
Popular generative model learning methods such as Generative Adversarial Networks (GANs), and Variational Autoencoders (VAE) enforce the latent representation to follow simple distributions such as isotropic Gaussian. In this paper, we argue that learning a complicated distribution over the latent space of an auto-encoder enables more accurate modeling of complicated data distributions. Based on this observation, we propose a two stage optimization procedure which maximizes an approximate implicit density model. We experimentally verify that our method outperforms GANs and VAEs on two image datasets (MNIST, CELEB-A). We also show that our approach is amenable to learning generative model for sequential data, by learning to generate speech and music.

Online Classification with Complex Metrics

We present a framework and analysis of consistent binary classification for complex and non-decomposable performance metrics such as the F-measure and the Jaccard measure. The proposed framework is general, as it applies to both batch and online learning, and to both linear and non-linear models. Our work follows recent results showing that the Bayes optimal classifier for many complex metrics is given by a thresholding of the conditional probability of the positive class. This manuscript extends this thresholding characterization -- showing that the utility is strictly locally quasi-concave with respect to the threshold for a wide range of models and performance metrics. This, in turn, motivates simple normalized gradient ascent updates for threshold estimation. We present a finite-sample regret analysis for the resulting procedure. In particular, the risk for the batch case converges to the Bayes risk at the same rate as that of the underlying conditional probability estimation, and the risk of proposed online algorithm converges at a rate that depends on the conditional probability estimation risk. For instance, in the special case where the conditional probability model is logistic regression, our procedure achieves $O(\frac{1}{\sqrt{n}})$ sample complexity, both for batch and online training. Empirical evaluation shows that the proposed algorithms out-perform alternatives in practice, with comparable or better prediction performance and reduced run time for various metrics and datasets.

Dependent relevance determination for smooth and structured sparse regression

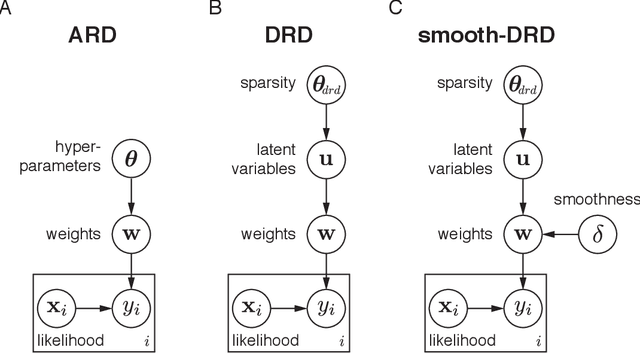
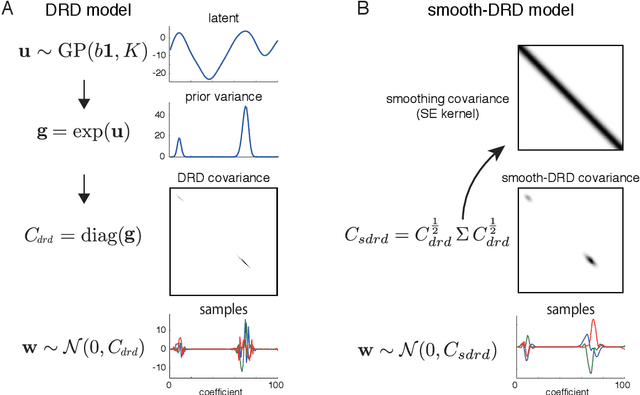
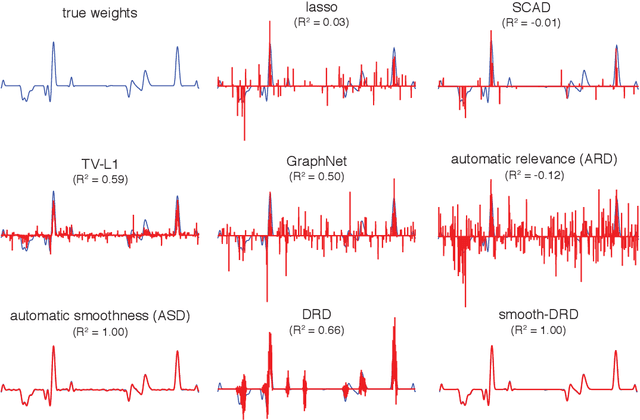
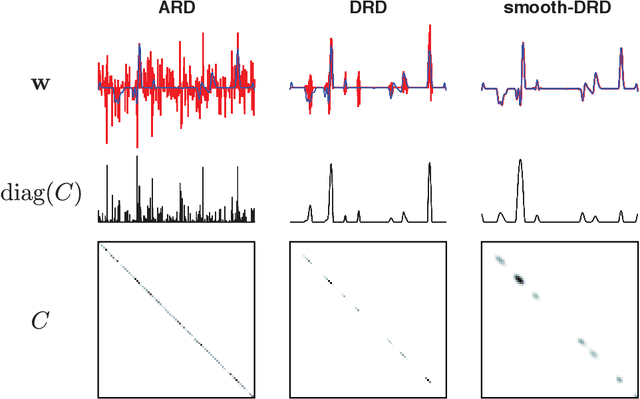
In many problem settings, parameter vectors are not merely sparse, but dependent in such a way that non-zero coefficients tend to cluster together. We refer to this form of dependency as "region sparsity". Classical sparse regression methods, such as the lasso and automatic relevance determination (ARD), which model parameters as independent a priori, and therefore do not exploit such dependencies. Here we introduce a hierarchical model for smooth, region-sparse weight vectors and tensors in a linear regression setting. Our approach represents a hierarchical extension of the relevance determination framework, where we add a transformed Gaussian process to model the dependencies between the prior variances of regression weights. We combine this with a structured model of the prior variances of Fourier coefficients, which eliminates unnecessary high frequencies. The resulting prior encourages weights to be region-sparse in two different bases simultaneously. We develop Laplace approximation and Monte Carlo Markov Chain (MCMC) sampling to provide efficient inference for the posterior. Furthermore, a two-stage convex relaxation of the Laplace approximation approach is also provided to relax the inevitable non-convexity during the optimization. We finally show substantial improvements over comparable methods for both simulated and real datasets from brain imaging.

Preference Completion from Partial Rankings

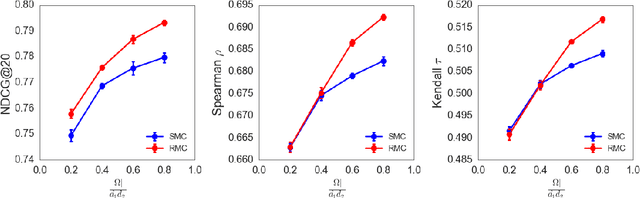
We propose a novel and efficient algorithm for the collaborative preference completion problem, which involves jointly estimating individualized rankings for a set of entities over a shared set of items, based on a limited number of observed affinity values. Our approach exploits the observation that while preferences are often recorded as numerical scores, the predictive quantity of interest is the underlying rankings. Thus, attempts to closely match the recorded scores may lead to overfitting and impair generalization performance. Instead, we propose an estimator that directly fits the underlying preference order, combined with nuclear norm constraints to encourage low--rank parameters. Besides (approximate) correctness of the ranking order, the proposed estimator makes no generative assumption on the numerical scores of the observations. One consequence is that the proposed estimator can fit any consistent partial ranking over a subset of the items represented as a directed acyclic graph (DAG), generalizing standard techniques that can only fit preference scores. Despite this generality, for supervision representing total or blockwise total orders, the computational complexity of our algorithm is within a $\log$ factor of the standard algorithms for nuclear norm regularization based estimates for matrix completion. We further show promising empirical results for a novel and challenging application of collaboratively ranking of the associations between brain--regions and cognitive neuroscience terms.

Information Projection and Approximate Inference for Structured Sparse Variables

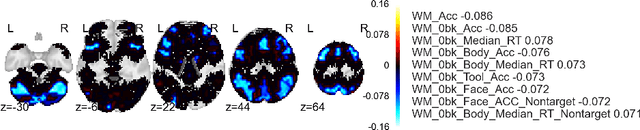
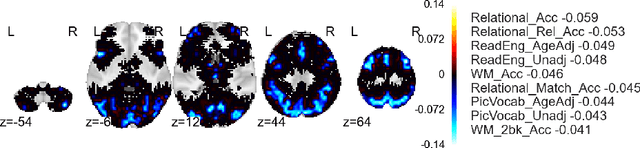
Approximate inference via information projection has been recently introduced as a general-purpose approach for efficient probabilistic inference given sparse variables. This manuscript goes beyond classical sparsity by proposing efficient algorithms for approximate inference via information projection that are applicable to any structure on the set of variables that admits enumeration using a \emph{matroid}. We show that the resulting information projection can be reduced to combinatorial submodular optimization subject to matroid constraints. Further, leveraging recent advances in submodular optimization, we provide an efficient greedy algorithm with strong optimization-theoretic guarantees. The class of probabilistic models that can be expressed in this way is quite broad and, as we show, includes group sparse regression, group sparse principal components analysis and sparse canonical correlation analysis, among others. Moreover, empirical results on simulated data and high dimensional neuroimaging data highlight the superior performance of the information projection approach as compared to established baselines for a range of probabilistic models.

A simple and provable algorithm for sparse diagonal CCA

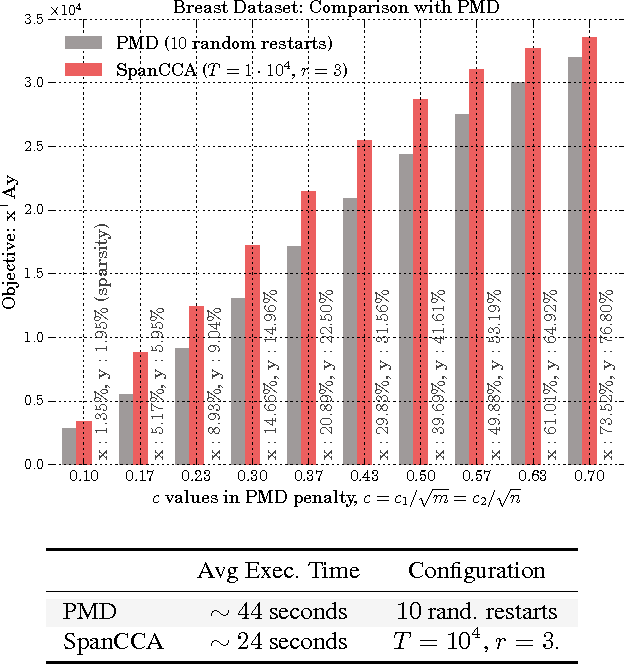
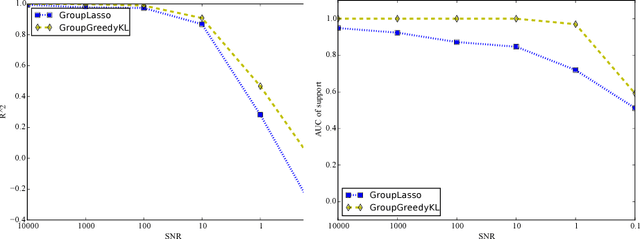
Given two sets of variables, derived from a common set of samples, sparse Canonical Correlation Analysis (CCA) seeks linear combinations of a small number of variables in each set, such that the induced canonical variables are maximally correlated. Sparse CCA is NP-hard. We propose a novel combinatorial algorithm for sparse diagonal CCA, i.e., sparse CCA under the additional assumption that variables within each set are standardized and uncorrelated. Our algorithm operates on a low rank approximation of the input data and its computational complexity scales linearly with the number of input variables. It is simple to implement, and parallelizable. In contrast to most existing approaches, our algorithm administers precise control on the sparsity of the extracted canonical vectors, and comes with theoretical data-dependent global approximation guarantees, that hinge on the spectrum of the input data. Finally, it can be straightforwardly adapted to other constrained variants of CCA enforcing structure beyond sparsity. We empirically evaluate the proposed scheme and apply it on a real neuroimaging dataset to investigate associations between brain activity and behavior measurements.

Generalized Linear Models for Aggregated Data

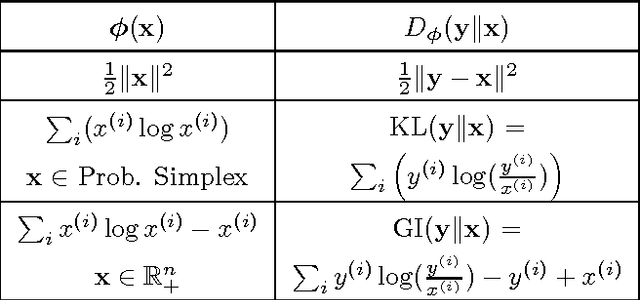
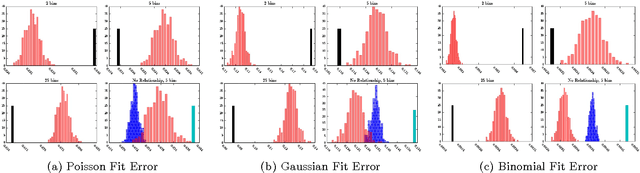
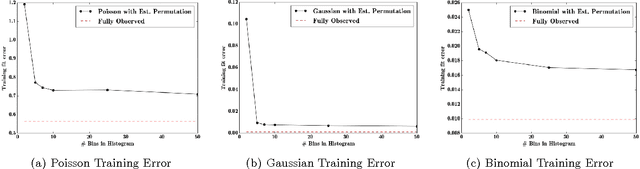
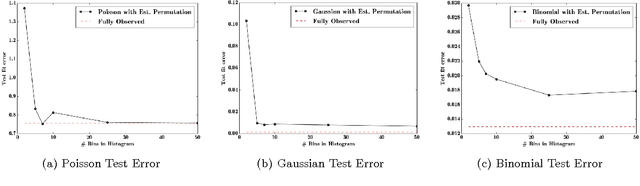
Databases in domains such as healthcare are routinely released to the public in aggregated form. Unfortunately, naive modeling with aggregated data may significantly diminish the accuracy of inferences at the individual level. This paper addresses the scenario where features are provided at the individual level, but the target variables are only available as histogram aggregates or order statistics. We consider a limiting case of generalized linear modeling when the target variables are only known up to permutation, and explore how this relates to permutation testing; a standard technique for assessing statistical dependency. Based on this relationship, we propose a simple algorithm to estimate the model parameters and individual level inferences via alternating imputation and standard generalized linear model fitting. Our results suggest the effectiveness of the proposed approach when, in the original data, permutation testing accurately ascertains the veracity of the linear relationship. The framework is extended to general histogram data with larger bins - with order statistics such as the median as a limiting case. Our experimental results on simulated data and aggregated healthcare data suggest a diminishing returns property with respect to the granularity of the histogram - when a linear relationship holds in the original data, the targets can be predicted accurately given relatively coarse histograms.

Optimal Decision-Theoretic Classification Using Non-Decomposable Performance Metrics

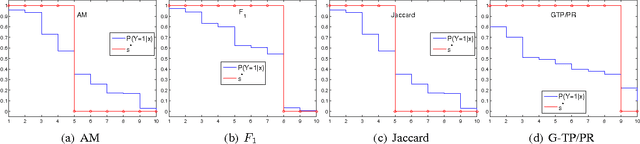
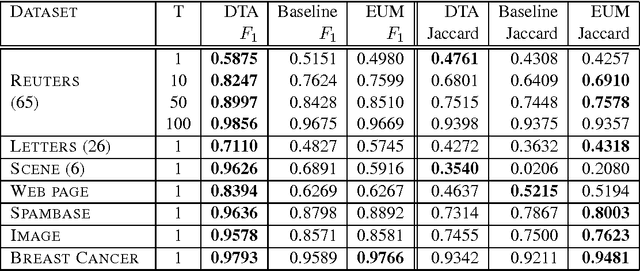
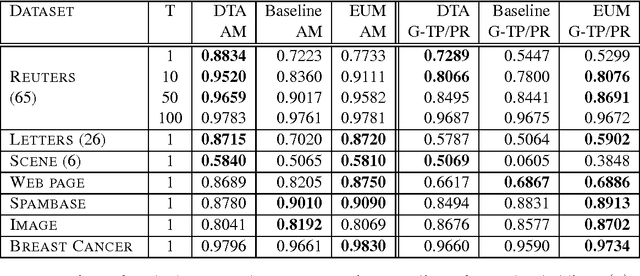
We provide a general theoretical analysis of expected out-of-sample utility, also referred to as decision-theoretic classification, for non-decomposable binary classification metrics such as F-measure and Jaccard coefficient. Our key result is that the expected out-of-sample utility for many performance metrics is provably optimized by a classifier which is equivalent to a signed thresholding of the conditional probability of the positive class. Our analysis bridges a gap in the literature on binary classification, revealed in light of recent results for non-decomposable metrics in population utility maximization style classification. Our results identify checkable properties of a performance metric which are sufficient to guarantee a probability ranking principle. We propose consistent estimators for optimal expected out-of-sample classification. As a consequence of the probability ranking principle, computational requirements can be reduced from exponential to cubic complexity in the general case, and further reduced to quadratic complexity in special cases. We provide empirical results on simulated and benchmark datasets evaluating the performance of the proposed algorithms for decision-theoretic classification and comparing them to baseline and state-of-the-art methods in population utility maximization for non-decomposable metrics.

A Constrained Matrix-Variate Gaussian Process for Transposable Data

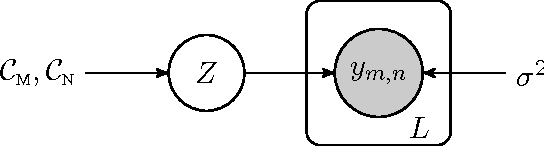
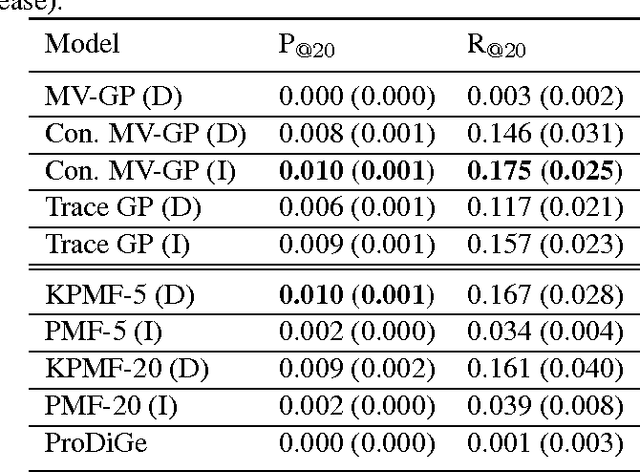
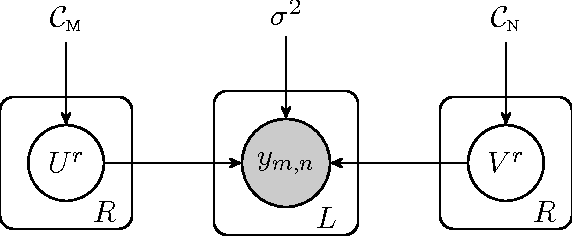
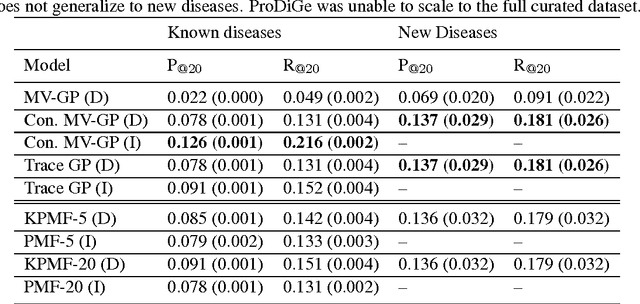
Transposable data represents interactions among two sets of entities, and are typically represented as a matrix containing the known interaction values. Additional side information may consist of feature vectors specific to entities corresponding to the rows and/or columns of such a matrix. Further information may also be available in the form of interactions or hierarchies among entities along the same mode (axis). We propose a novel approach for modeling transposable data with missing interactions given additional side information. The interactions are modeled as noisy observations from a latent noise free matrix generated from a matrix-variate Gaussian process. The construction of row and column covariances using side information provides a flexible mechanism for specifying a-priori knowledge of the row and column correlations in the data. Further, the use of such a prior combined with the side information enables predictions for new rows and columns not observed in the training data. In this work, we combine the matrix-variate Gaussian process model with low rank constraints. The constrained Gaussian process approach is applied to the prediction of hidden associations between genes and diseases using a small set of observed associations as well as prior covariances induced by gene-gene interaction networks and disease ontologies. The proposed approach is also applied to recommender systems data which involves predicting the item ratings of users using known associations as well as prior covariances induced by social networks. We present experimental results that highlight the performance of constrained matrix-variate Gaussian process as compared to state of the art approaches in each domain.