Cheng Lee
A Constrained Matrix-Variate Gaussian Process for Transposable Data
Apr 27, 2014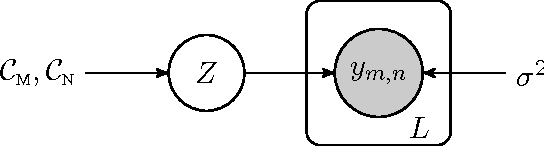
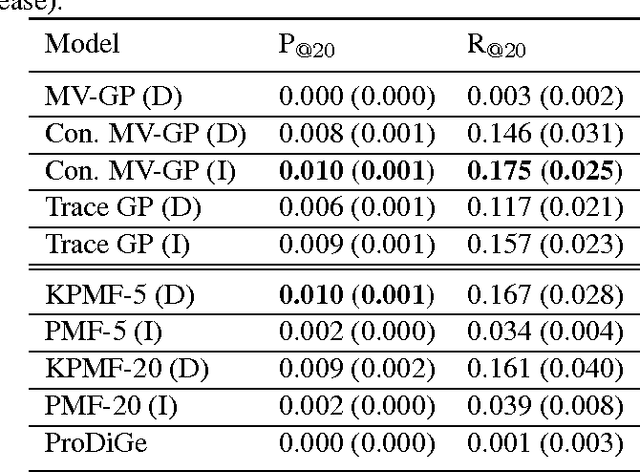
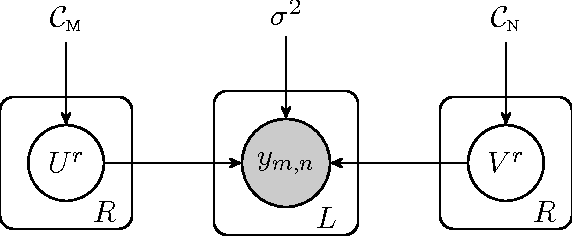
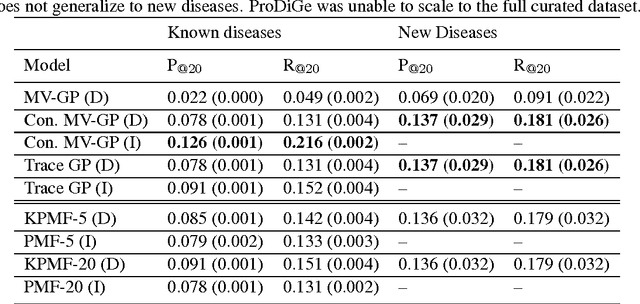
Abstract:Transposable data represents interactions among two sets of entities, and are typically represented as a matrix containing the known interaction values. Additional side information may consist of feature vectors specific to entities corresponding to the rows and/or columns of such a matrix. Further information may also be available in the form of interactions or hierarchies among entities along the same mode (axis). We propose a novel approach for modeling transposable data with missing interactions given additional side information. The interactions are modeled as noisy observations from a latent noise free matrix generated from a matrix-variate Gaussian process. The construction of row and column covariances using side information provides a flexible mechanism for specifying a-priori knowledge of the row and column correlations in the data. Further, the use of such a prior combined with the side information enables predictions for new rows and columns not observed in the training data. In this work, we combine the matrix-variate Gaussian process model with low rank constraints. The constrained Gaussian process approach is applied to the prediction of hidden associations between genes and diseases using a small set of observed associations as well as prior covariances induced by gene-gene interaction networks and disease ontologies. The proposed approach is also applied to recommender systems data which involves predicting the item ratings of users using known associations as well as prior covariances induced by social networks. We present experimental results that highlight the performance of constrained matrix-variate Gaussian process as compared to state of the art approaches in each domain.
The trace norm constrained matrix-variate Gaussian process for multitask bipartite ranking
Feb 11, 2013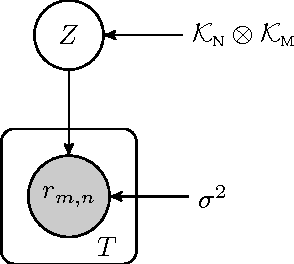
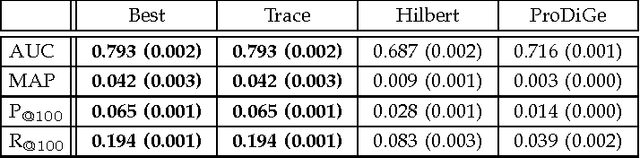
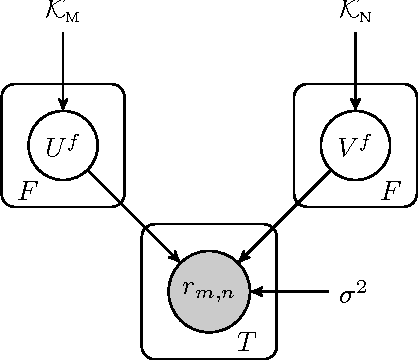
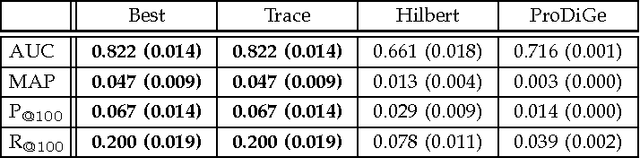
Abstract:We propose a novel hierarchical model for multitask bipartite ranking. The proposed approach combines a matrix-variate Gaussian process with a generative model for task-wise bipartite ranking. In addition, we employ a novel trace constrained variational inference approach to impose low rank structure on the posterior matrix-variate Gaussian process. The resulting posterior covariance function is derived in closed form, and the posterior mean function is the solution to a matrix-variate regression with a novel spectral elastic net regularizer. Further, we show that variational inference for the trace constrained matrix-variate Gaussian process combined with maximum likelihood parameter estimation for the bipartite ranking model is jointly convex. Our motivating application is the prioritization of candidate disease genes. The goal of this task is to aid the identification of unobserved associations between human genes and diseases using a small set of observed associations as well as kernels induced by gene-gene interaction networks and disease ontologies. Our experimental results illustrate the performance of the proposed model on real world datasets. Moreover, we find that the resulting low rank solution improves the computational scalability of training and testing as compared to baseline models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge