Bowei Yan
Consistent Classification with Generalized Metrics
Aug 24, 2019
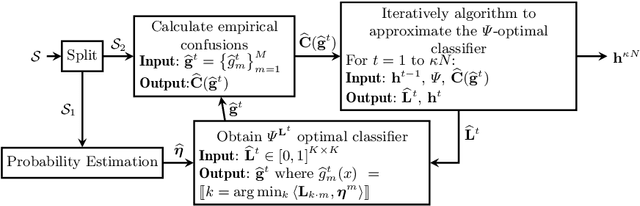
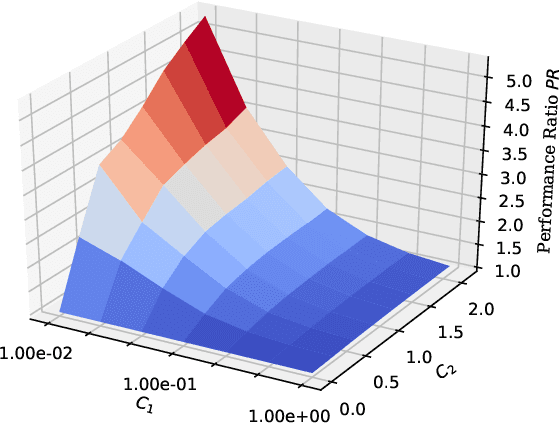
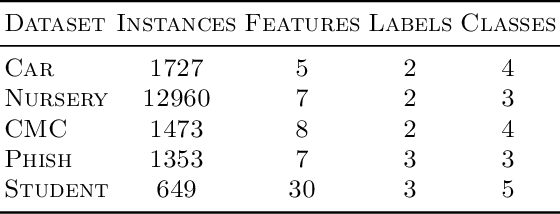
Abstract:We propose a framework for constructing and analyzing multiclass and multioutput classification metrics, i.e., involving multiple, possibly correlated multiclass labels. Our analysis reveals novel insights on the geometry of feasible confusion tensors -- including necessary and sufficient conditions for the equivalence between optimizing an arbitrary non-decomposable metric and learning a weighted classifier. Further, we analyze averaging methodologies commonly used to compute multioutput metrics and characterize the corresponding Bayes optimal classifiers. We show that the plug-in estimator based on this characterization is consistent and is easily implemented as a post-processing rule. Empirical results on synthetic and benchmark datasets support the theoretical findings.
Binary Classification with Karmic, Threshold-Quasi-Concave Metrics
Jun 02, 2018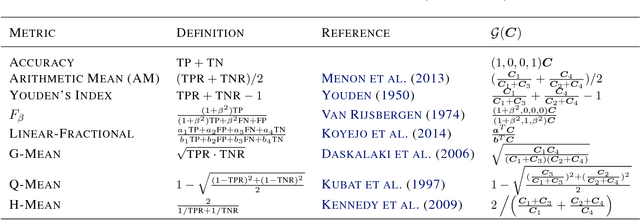
Abstract:Complex performance measures, beyond the popular measure of accuracy, are increasingly being used in the context of binary classification. These complex performance measures are typically not even decomposable, that is, the loss evaluated on a batch of samples cannot typically be expressed as a sum or average of losses evaluated at individual samples, which in turn requires new theoretical and methodological developments beyond standard treatments of supervised learning. In this paper, we advance this understanding of binary classification for complex performance measures by identifying two key properties: a so-called Karmic property, and a more technical threshold-quasi-concavity property, which we show is milder than existing structural assumptions imposed on performance measures. Under these properties, we show that the Bayes optimal classifier is a threshold function of the conditional probability of positive class. We then leverage this result to come up with a computationally practical plug-in classifier, via a novel threshold estimator, and further, provide a novel statistical analysis of classification error with respect to complex performance measures.
Covariate Regularized Community Detection in Sparse Graphs
Apr 25, 2018
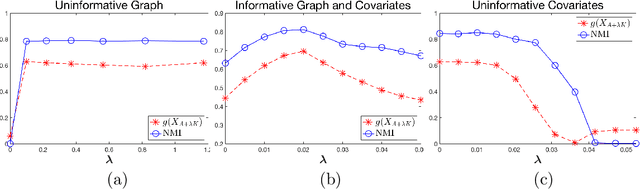

Abstract:In this paper, we investigate community detection in networks in the presence of node covariates. In many instances, covariates and networks individually only give a partial view of the cluster structure. One needs to jointly infer the full cluster structure by considering both. In statistics, an emerging body of work has been focused on combining information from both the edges in the network and the node covariates to infer community memberships. However, so far the theoretical guarantees have been established in the dense regime, where the network can lead to perfect clustering under a broad parameter regime, and hence the role of covariates is often not clear. In this paper, we examine sparse networks in conjunction with finite dimensional sub-gaussian mixtures as covariates under moderate separation conditions. In this setting each individual source can only cluster a non-vanishing fraction of nodes correctly. We propose a simple optimization framework which provably improves clustering accuracy when the two sources carry partial information about the cluster memberships, and hence perform poorly on their own. Our optimization problem can be solved using scalable convex optimization algorithms. Using a variety of simulated and real data examples, we show that the proposed method outperforms other existing methodology.
Provable Estimation of the Number of Blocks in Block Models
Mar 18, 2018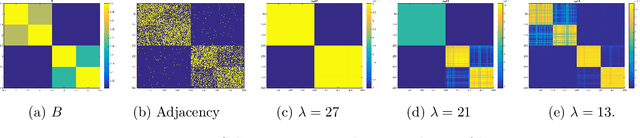
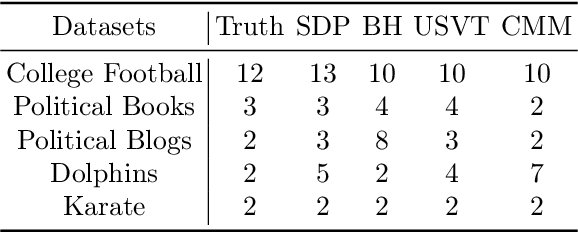
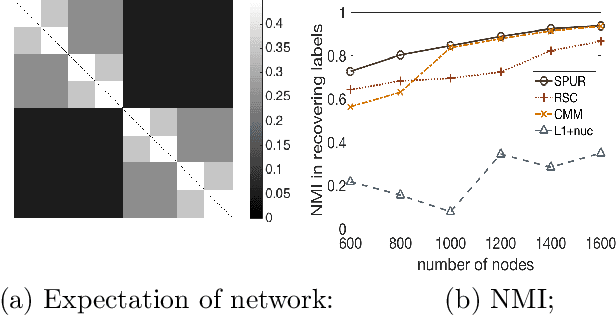
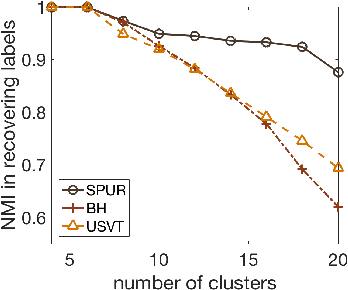
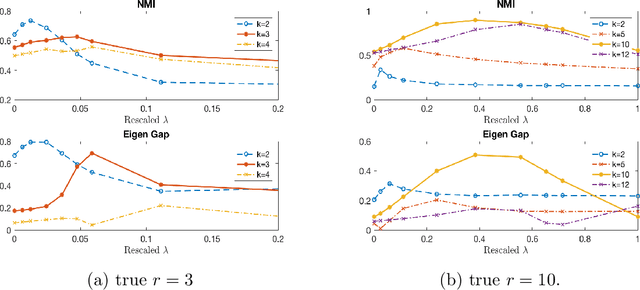
Abstract:Community detection is a fundamental unsupervised learning problem for unlabeled networks which has a broad range of applications. Many community detection algorithms assume that the number of clusters $r$ is known apriori. In this paper, we propose an approach based on semi-definite relaxations, which does not require prior knowledge of model parameters like many existing convex relaxation methods and recovers the number of clusters and the clustering matrix exactly under a broad parameter regime, with probability tending to one. On a variety of simulated and real data experiments, we show that the proposed method often outperforms state-of-the-art techniques for estimating the number of clusters.
Online Classification with Complex Metrics
Feb 10, 2018Abstract:We present a framework and analysis of consistent binary classification for complex and non-decomposable performance metrics such as the F-measure and the Jaccard measure. The proposed framework is general, as it applies to both batch and online learning, and to both linear and non-linear models. Our work follows recent results showing that the Bayes optimal classifier for many complex metrics is given by a thresholding of the conditional probability of the positive class. This manuscript extends this thresholding characterization -- showing that the utility is strictly locally quasi-concave with respect to the threshold for a wide range of models and performance metrics. This, in turn, motivates simple normalized gradient ascent updates for threshold estimation. We present a finite-sample regret analysis for the resulting procedure. In particular, the risk for the batch case converges to the Bayes risk at the same rate as that of the underlying conditional probability estimation, and the risk of proposed online algorithm converges at a rate that depends on the conditional probability estimation risk. For instance, in the special case where the conditional probability model is logistic regression, our procedure achieves $O(\frac{1}{\sqrt{n}})$ sample complexity, both for batch and online training. Empirical evaluation shows that the proposed algorithms out-perform alternatives in practice, with comparable or better prediction performance and reduced run time for various metrics and datasets.
Convergence Analysis of Gradient EM for Multi-component Gaussian Mixture
Dec 04, 2017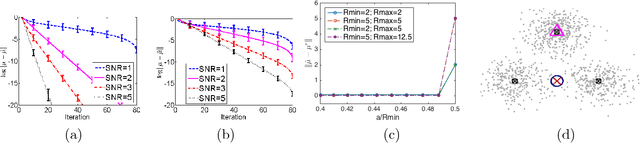
Abstract:In this paper, we study convergence properties of the gradient Expectation-Maximization algorithm \cite{lange1995gradient} for Gaussian Mixture Models for general number of clusters and mixing coefficients. We derive the convergence rate depending on the mixing coefficients, minimum and maximum pairwise distances between the true centers and dimensionality and number of components; and obtain a near-optimal local contraction radius. While there have been some recent notable works that derive local convergence rates for EM in the two equal mixture symmetric GMM, in the more general case, the derivations need structurally different and non-trivial arguments. We use recent tools from learning theory and empirical processes to achieve our theoretical results.
On Robustness of Kernel Clustering
Dec 02, 2016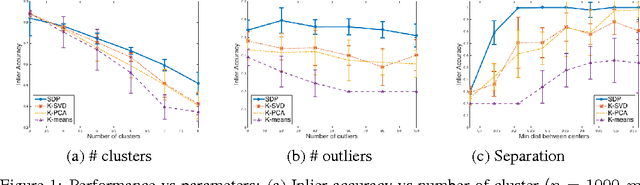
Abstract:Clustering is one of the most important unsupervised problems in machine learning and statistics. Among many existing algorithms, kernel k-means has drawn much research attention due to its ability to find non-linear cluster boundaries and its inherent simplicity. There are two main approaches for kernel k-means: SVD of the kernel matrix and convex relaxations. Despite the attention kernel clustering has received both from theoretical and applied quarters, not much is known about robustness of the methods. In this paper we first introduce a semidefinite programming relaxation for the kernel clustering problem, then prove that under a suitable model specification, both the K-SVD and SDP approaches are consistent in the limit, albeit SDP is strongly consistent, i.e. achieves exact recovery, whereas K-SVD is weakly consistent, i.e. the fraction of misclassified nodes vanish.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge