Partially adaptive filtering using randomized projections
Paper and Code
Mar 21, 2022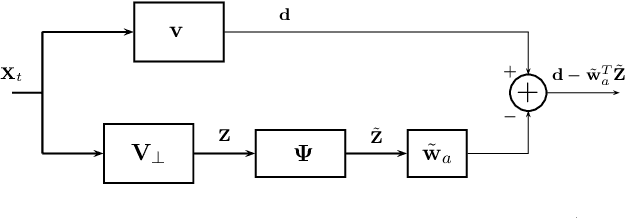
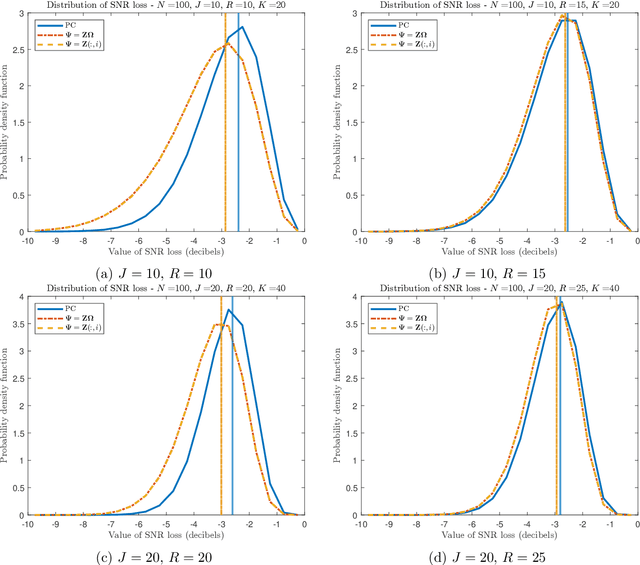
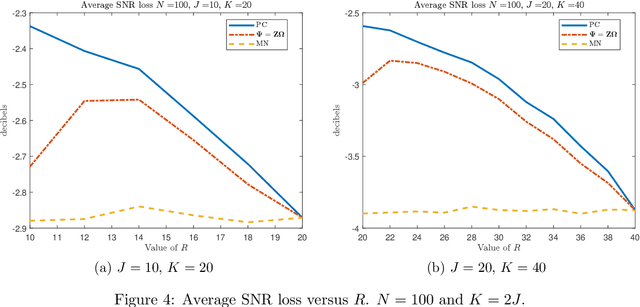
This short note addresses the design of a partially adaptive filter to retrieve a signal of interest in the presence of strong low-rank interference and thermal noise. We consider a generalized sidelobe canceler implementation where the dimension-reducing transformation is build resorting to ideas borrowed from randomized matrix approximations. More precisely, the main subspace of the auxiliary data $Z$ is approximated by $Z\Omega$ where $\Omega$ is a random matrix or a matrix that picks at random columns of $Z$. These transformations do not require eigenvalue decomposition, yet they provide performance similar to those of a principal component filter.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge