A short overview of adaptive multichannel filters SNR loss analysis
Paper and Code
Mar 03, 2021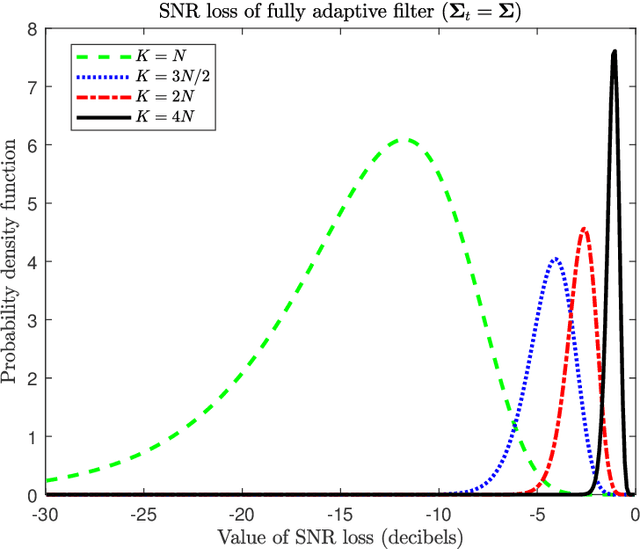
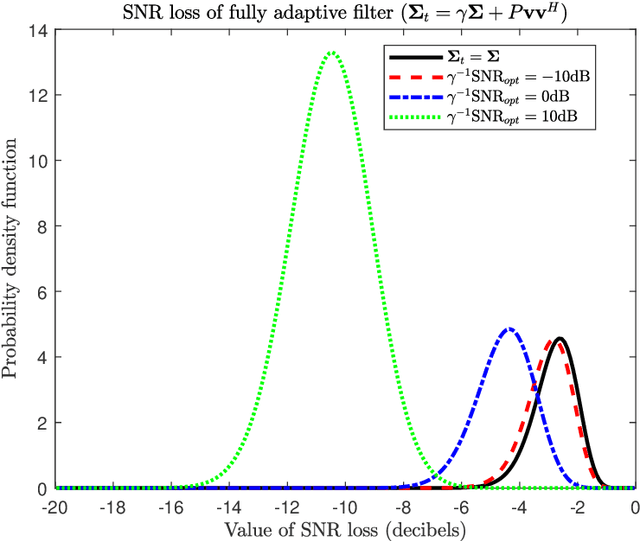
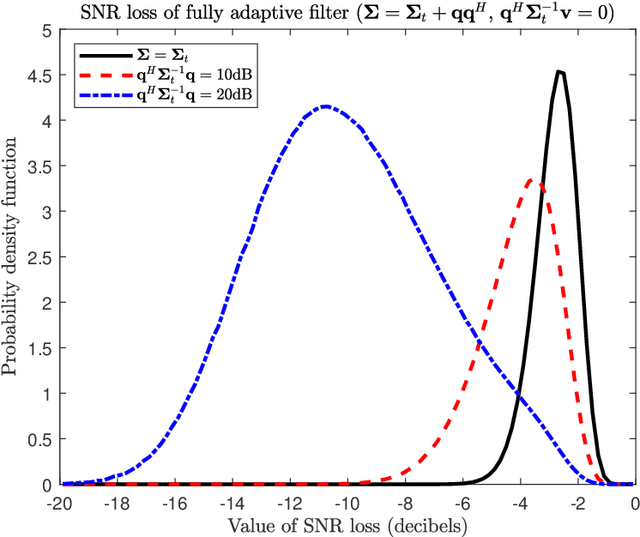
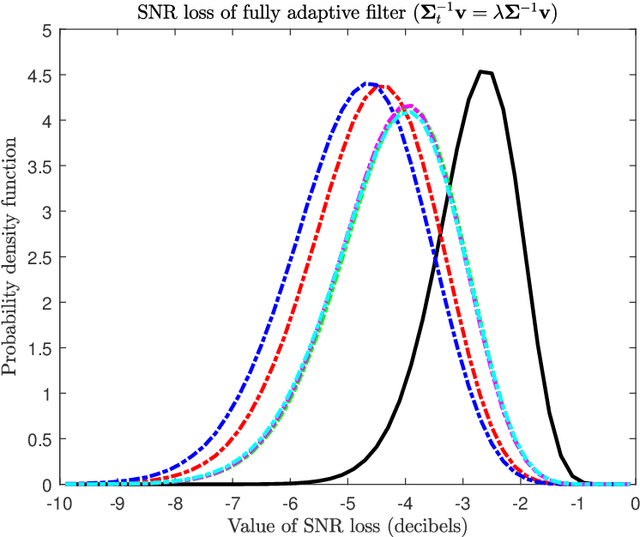
Many multichannel systems use a linear filter to retrieve a signal of interest corrupted by noise whose statistics are partly unknown. The optimal filter in Gaussian noise requires knowledge of the noise covariance matrix $\Sigma$ and in practice the latter is estimated from a set of training samples. An important issue concerns the characterization of the performance of such adaptive filters. This is generally achieved using as figure of merit the ratio of the signal to noise ratio (SNR) at the output of the adaptive filter to the SNR obtained with the clairvoyant -- known $\Sigma$ -- filter. This problem has been studied extensively since the seventies and this document presents a concise overview of results published in the literature. We consider various cases about the training samples covariance matrix and we investigate fully adaptive, partially adaptive and regularized filters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge