On the distributions of some statistics related to adaptive filters trained with $t$-distributed samples

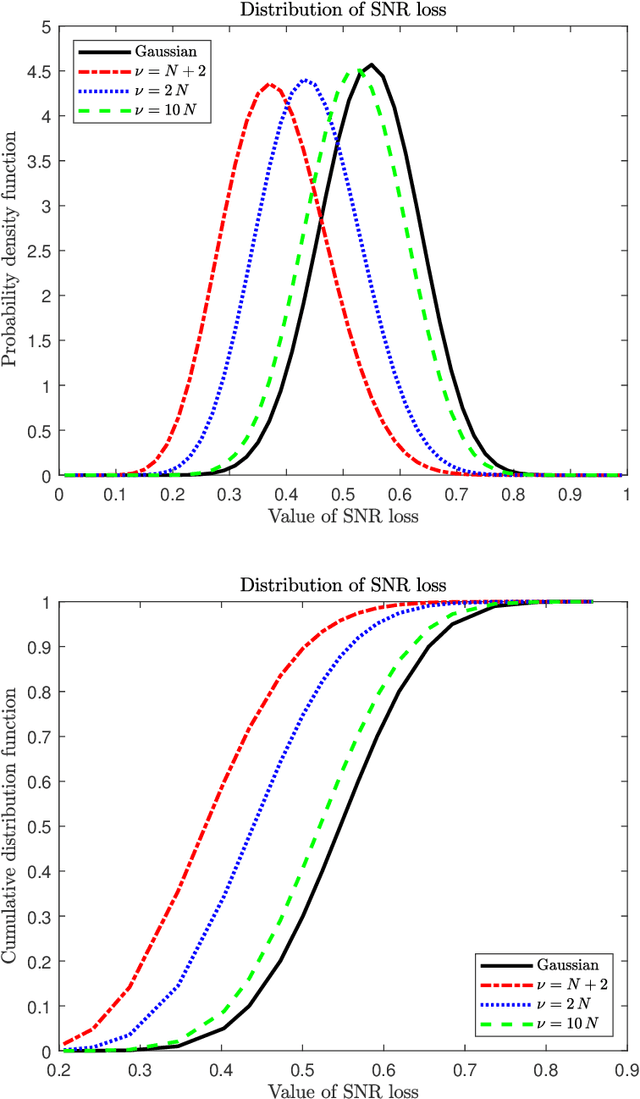
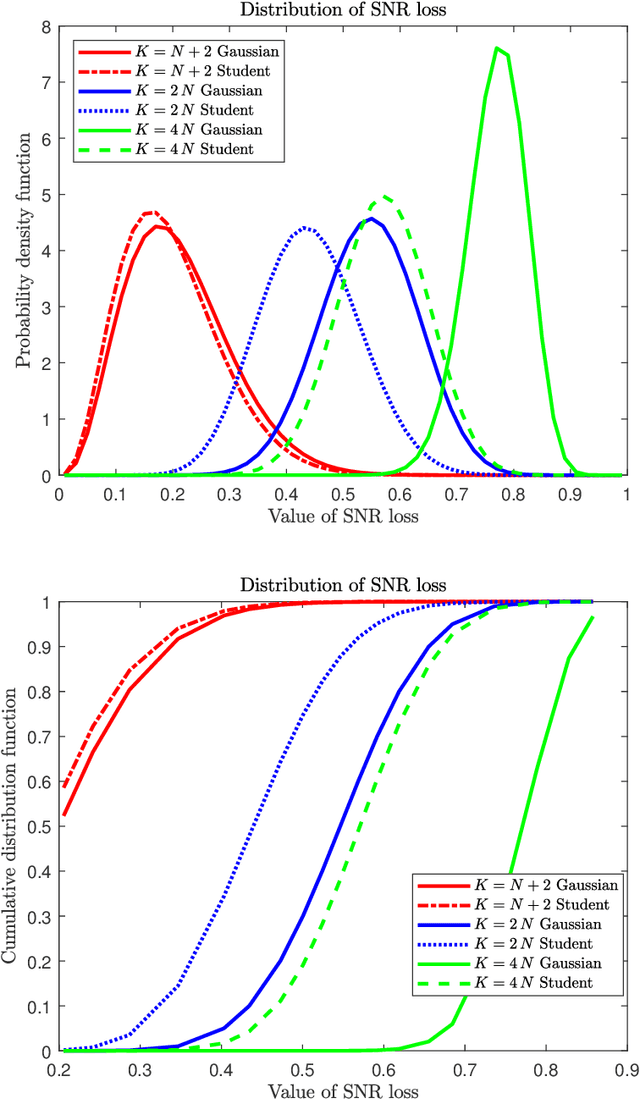
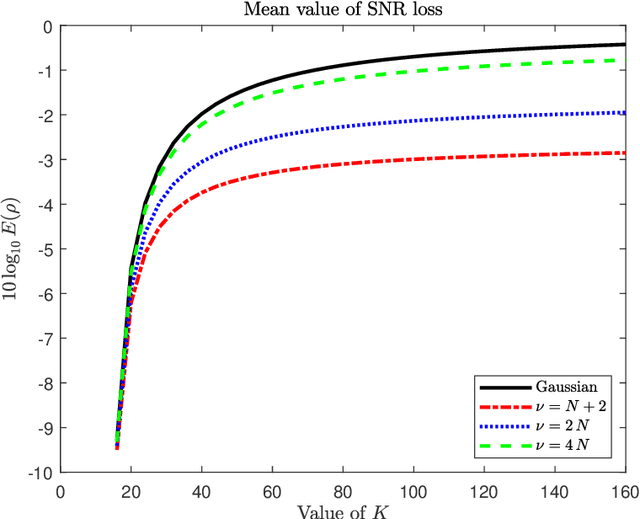
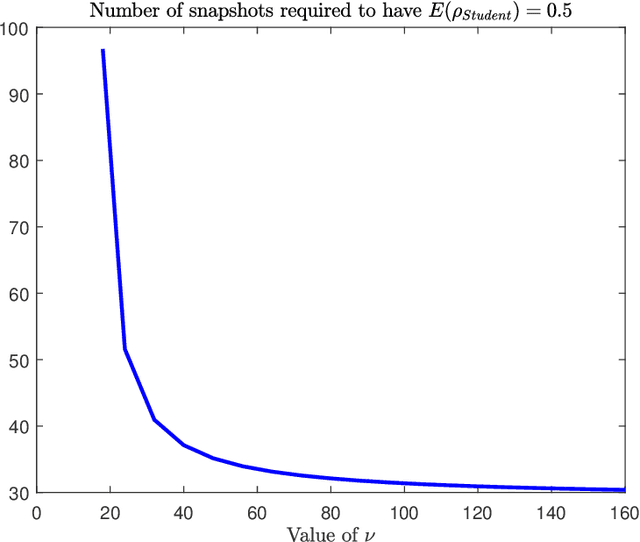
In this paper we analyze the behavior of adaptive filters or detectors when they are trained with $t$-distributed samples rather than Gaussian distributed samples. More precisely we investigate the impact on the distribution of some relevant statistics including the signal to noise ratio loss and the Gaussian generalized likelihood ratio test. Some properties of partitioned complex $F$ distributed matrices are derived which enable to obtain statistical representations in terms of independent chi-square distributed random variables. These representations are compared with their Gaussian counterparts and numerical simulations illustrate and quantify the induced degradation.