Sequential Neural Models with Stochastic Layers

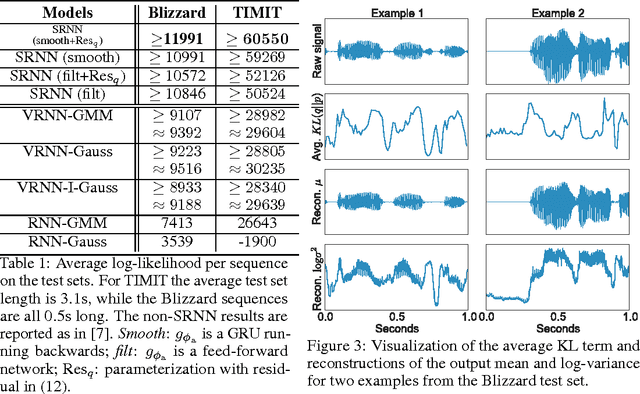
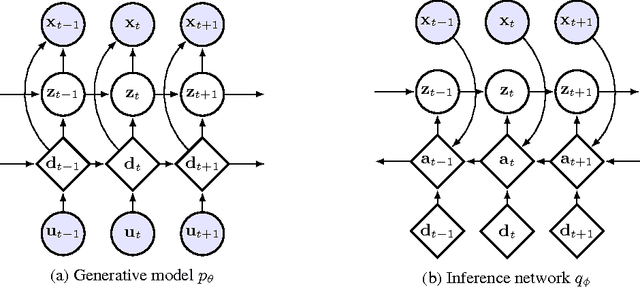
How can we efficiently propagate uncertainty in a latent state representation with recurrent neural networks? This paper introduces stochastic recurrent neural networks which glue a deterministic recurrent neural network and a state space model together to form a stochastic and sequential neural generative model. The clear separation of deterministic and stochastic layers allows a structured variational inference network to track the factorization of the model's posterior distribution. By retaining both the nonlinear recursive structure of a recurrent neural network and averaging over the uncertainty in a latent path, like a state space model, we improve the state of the art results on the Blizzard and TIMIT speech modeling data sets by a large margin, while achieving comparable performances to competing methods on polyphonic music modeling.

Neural Machine Translation with Characters and Hierarchical Encoding

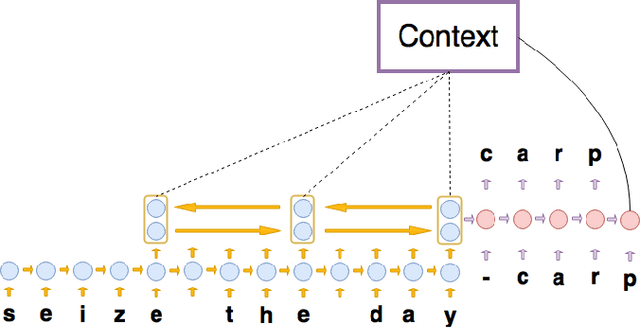
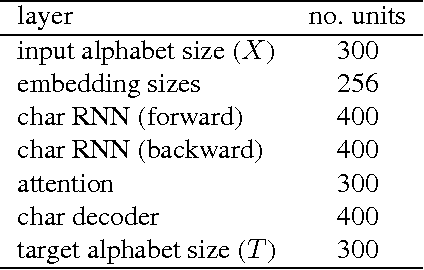
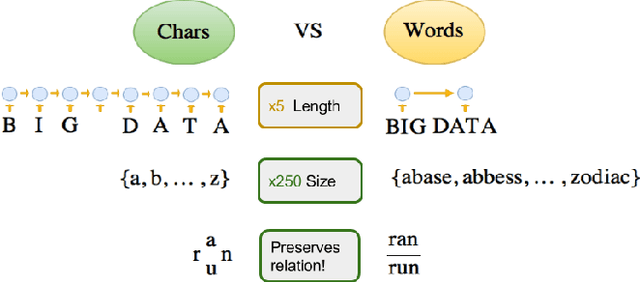
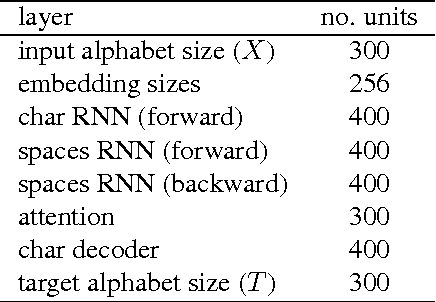
Most existing Neural Machine Translation models use groups of characters or whole words as their unit of input and output. We propose a model with a hierarchical char2word encoder, that takes individual characters both as input and output. We first argue that this hierarchical representation of the character encoder reduces computational complexity, and show that it improves translation performance. Secondly, by qualitatively studying attention plots from the decoder we find that the model learns to compress common words into a single embedding whereas rare words, such as names and places, are represented character by character.

Self-Averaging Expectation Propagation

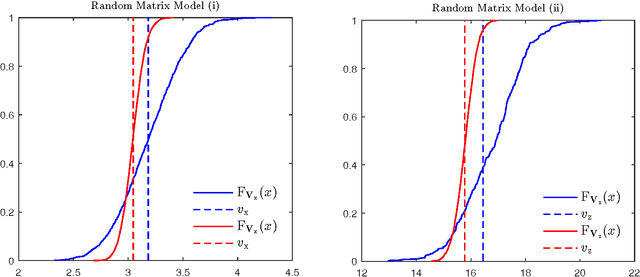
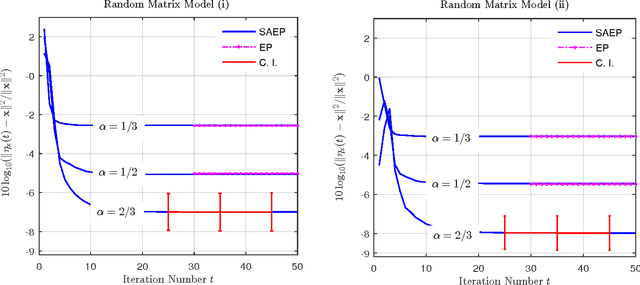
We investigate the problem of approximate Bayesian inference for a general class of observation models by means of the expectation propagation (EP) framework for large systems under some statistical assumptions. Our approach tries to overcome the numerical bottleneck of EP caused by the inversion of large matrices. Assuming that the measurement matrices are realizations of specific types of ensembles we use the concept of freeness from random matrix theory to show that the EP cavity variances exhibit an asymptotic self-averaging property. They can be pre-computed using specific generating functions, i.e. the R- and/or S-transforms in free probability, which do not require matrix inversions. Our approach extends the framework of (generalized) approximate message passing -- assumes zero-mean iid entries of the measurement matrix -- to a general class of random matrix ensembles. The generalization is via a simple formulation of the R- and/or S-transforms of the limiting eigenvalue distribution of the Gramian of the measurement matrix. We demonstrate the performance of our approach on a signal recovery problem of nonlinear compressed sensing and compare it with that of EP.

An Adaptive Resample-Move Algorithm for Estimating Normalizing Constants

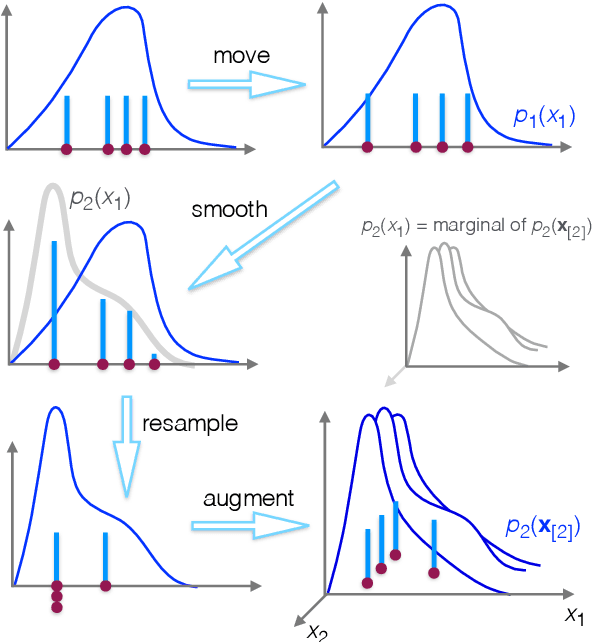
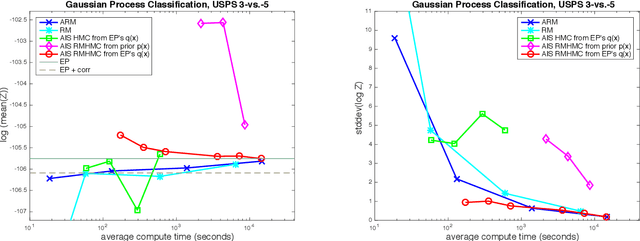
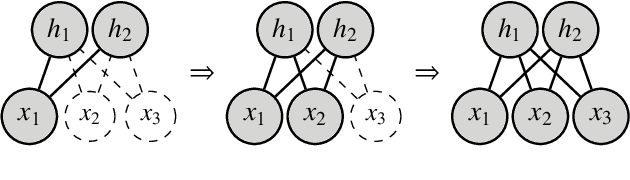
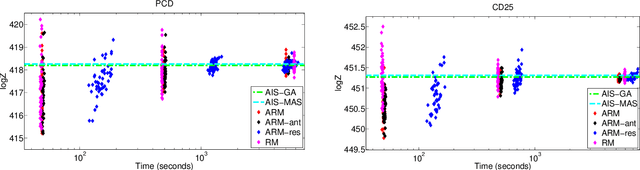
The estimation of normalizing constants is a fundamental step in probabilistic model comparison. Sequential Monte Carlo methods may be used for this task and have the advantage of being inherently parallelizable. However, the standard choice of using a fixed number of particles at each iteration is suboptimal because some steps will contribute disproportionately to the variance of the estimate. We introduce an adaptive version of the Resample-Move algorithm, in which the particle set is adaptively expanded whenever a better approximation of an intermediate distribution is needed. The algorithm builds on the expression for the optimal number of particles and the corresponding minimum variance found under ideal conditions. Benchmark results on challenging Gaussian Process Classification and Restricted Boltzmann Machine applications show that Adaptive Resample-Move (ARM) estimates the normalizing constant with a smaller variance, using less computational resources, than either Resample-Move with a fixed number of particles or Annealed Importance Sampling. A further advantage over Annealed Importance Sampling is that ARM is easier to tune.

Auxiliary Deep Generative Models

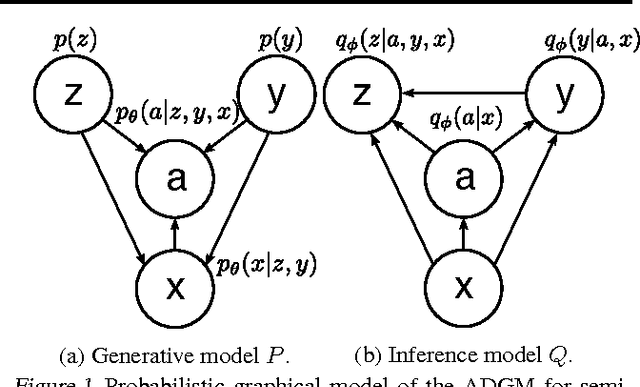
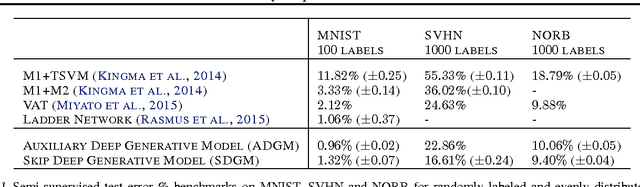
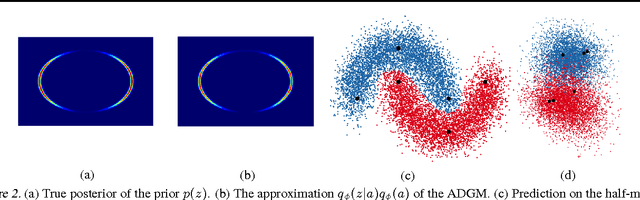
Deep generative models parameterized by neural networks have recently achieved state-of-the-art performance in unsupervised and semi-supervised learning. We extend deep generative models with auxiliary variables which improves the variational approximation. The auxiliary variables leave the generative model unchanged but make the variational distribution more expressive. Inspired by the structure of the auxiliary variable we also propose a model with two stochastic layers and skip connections. Our findings suggest that more expressive and properly specified deep generative models converge faster with better results. We show state-of-the-art performance within semi-supervised learning on MNIST, SVHN and NORB datasets.

Ladder Variational Autoencoders

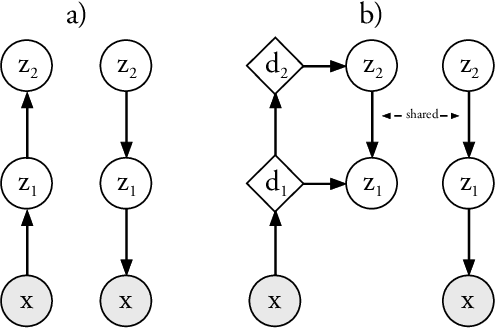
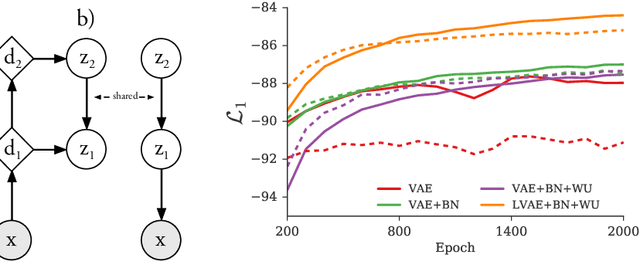
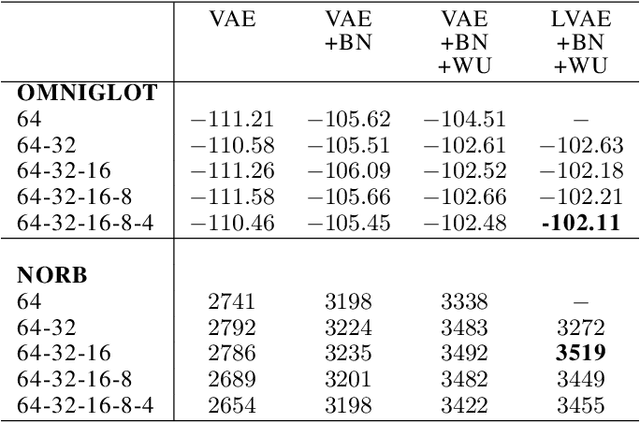
Variational Autoencoders are powerful models for unsupervised learning. However deep models with several layers of dependent stochastic variables are difficult to train which limits the improvements obtained using these highly expressive models. We propose a new inference model, the Ladder Variational Autoencoder, that recursively corrects the generative distribution by a data dependent approximate likelihood in a process resembling the recently proposed Ladder Network. We show that this model provides state of the art predictive log-likelihood and tighter log-likelihood lower bound compared to the purely bottom-up inference in layered Variational Autoencoders and other generative models. We provide a detailed analysis of the learned hierarchical latent representation and show that our new inference model is qualitatively different and utilizes a deeper more distributed hierarchy of latent variables. Finally, we observe that batch normalization and deterministic warm-up (gradually turning on the KL-term) are crucial for training variational models with many stochastic layers.

Bayesian leave-one-out cross-validation approximations for Gaussian latent variable models

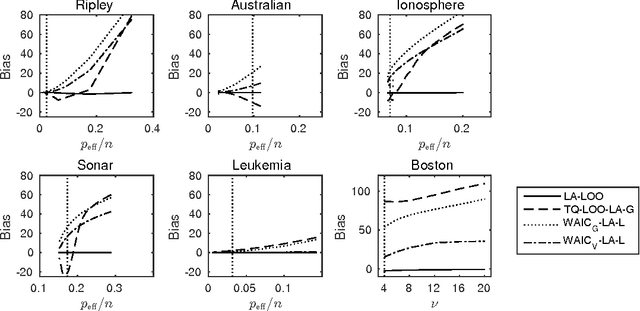
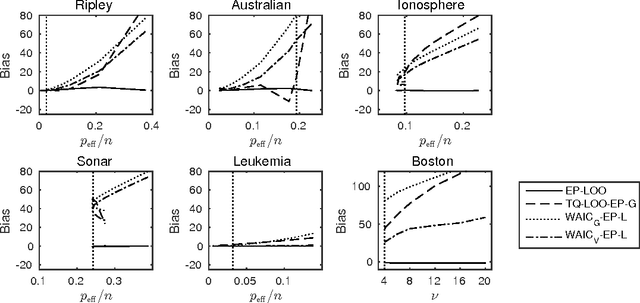
The future predictive performance of a Bayesian model can be estimated using Bayesian cross-validation. In this article, we consider Gaussian latent variable models where the integration over the latent values is approximated using the Laplace method or expectation propagation (EP). We study the properties of several Bayesian leave-one-out (LOO) cross-validation approximations that in most cases can be computed with a small additional cost after forming the posterior approximation given the full data. Our main objective is to assess the accuracy of the approximative LOO cross-validation estimators. That is, for each method (Laplace and EP) we compare the approximate fast computation with the exact brute force LOO computation. Secondarily, we evaluate the accuracy of the Laplace and EP approximations themselves against a ground truth established through extensive Markov chain Monte Carlo simulation. Our empirical results show that the approach based upon a Gaussian approximation to the LOO marginal distribution (the so-called cavity distribution) gives the most accurate and reliable results among the fast methods.

Autoencoding beyond pixels using a learned similarity metric

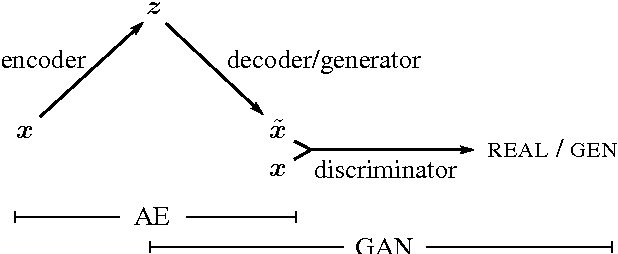
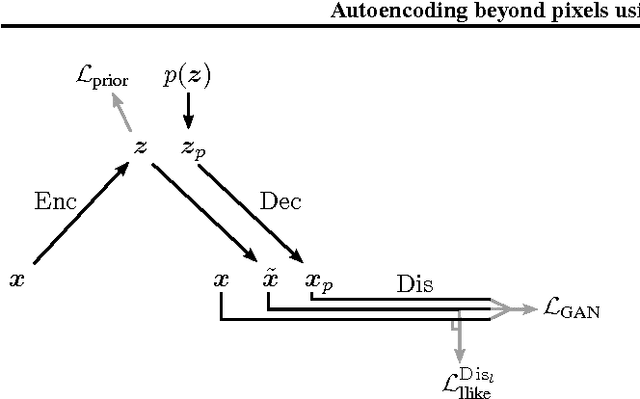
We present an autoencoder that leverages learned representations to better measure similarities in data space. By combining a variational autoencoder with a generative adversarial network we can use learned feature representations in the GAN discriminator as basis for the VAE reconstruction objective. Thereby, we replace element-wise errors with feature-wise errors to better capture the data distribution while offering invariance towards e.g. translation. We apply our method to images of faces and show that it outperforms VAEs with element-wise similarity measures in terms of visual fidelity. Moreover, we show that the method learns an embedding in which high-level abstract visual features (e.g. wearing glasses) can be modified using simple arithmetic.

Recurrent Spatial Transformer Networks

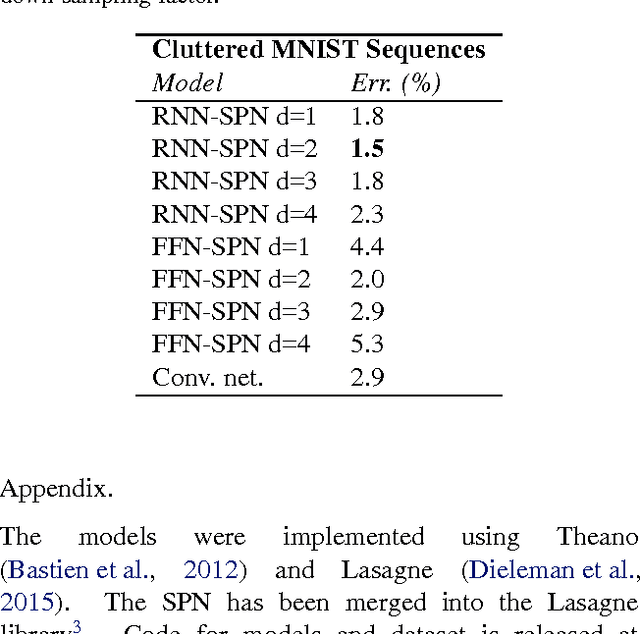
We integrate the recently proposed spatial transformer network (SPN) [Jaderberg et. al 2015] into a recurrent neural network (RNN) to form an RNN-SPN model. We use the RNN-SPN to classify digits in cluttered MNIST sequences. The proposed model achieves a single digit error of 1.5% compared to 2.9% for a convolutional networks and 2.0% for convolutional networks with SPN layers. The SPN outputs a zoomed, rotated and skewed version of the input image. We investigate different down-sampling factors (ratio of pixel in input and output) for the SPN and show that the RNN-SPN model is able to down-sample the input images without deteriorating performance. The down-sampling in RNN-SPN can be thought of as adaptive down-sampling that minimizes the information loss in the regions of interest. We attribute the superior performance of the RNN-SPN to the fact that it can attend to a sequence of regions of interest.

Spatio-temporal Spike and Slab Priors for Multiple Measurement Vector Problems

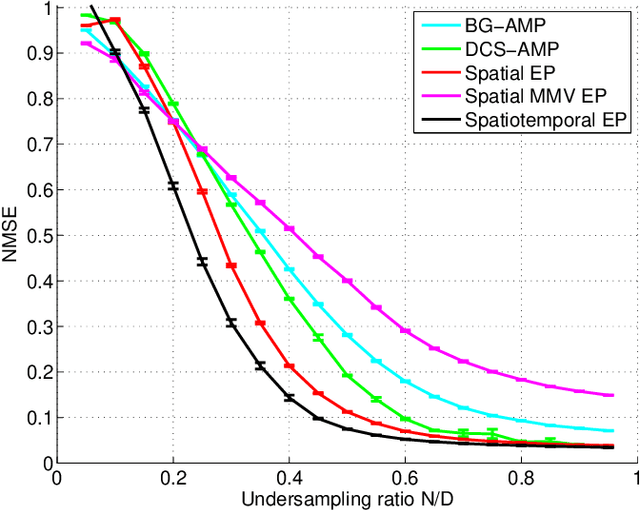
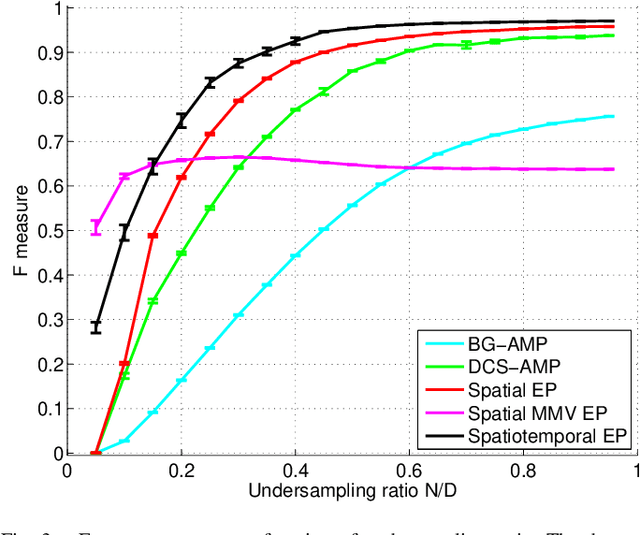
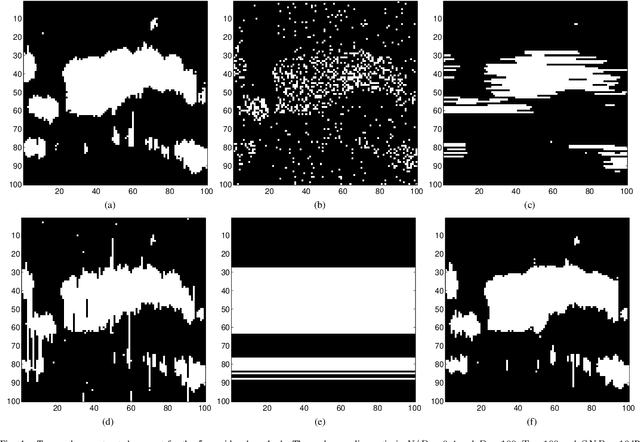
We are interested in solving the multiple measurement vector (MMV) problem for instances, where the underlying sparsity pattern exhibit spatio-temporal structure motivated by the electroencephalogram (EEG) source localization problem. We propose a probabilistic model that takes this structure into account by generalizing the structured spike and slab prior and the associated Expectation Propagation inference scheme. Based on numerical experiments, we demonstrate the viability of the model and the approximate inference scheme.