BIVA: A Very Deep Hierarchy of Latent Variables for Generative Modeling

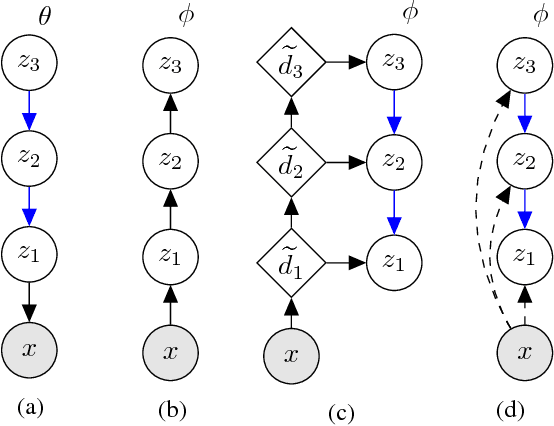
With the introduction of the variational autoencoder (VAE), probabilistic latent variable models have received renewed attention as powerful generative models. However, their performance in terms of test likelihood and quality of generated samples has been surpassed by autoregressive models without stochastic units. Furthermore, flow-based models have recently been shown to be an attractive alternative that scales well to high-dimensional data. In this paper we close the performance gap by constructing VAE models that can effectively utilize a deep hierarchy of stochastic variables and model complex covariance structures. We introduce the Bidirectional-Inference Variational Autoencoder (BIVA), characterized by a skip-connected generative model and an inference network formed by a bidirectional stochastic inference path. We show that BIVA reaches state-of-the-art test likelihoods, generates sharp and coherent natural images, and uses the hierarchy of latent variables to capture different aspects of the data distribution. We observe that BIVA, in contrast to recent results, can be used for anomaly detection. We attribute this to the hierarchy of latent variables which is able to extract high-level semantic features. Finally, we extend BIVA to semi-supervised classification tasks and show that it performs comparably to state-of-the-art results by generative adversarial networks.

An Efficient Implementation of Riemannian Manifold Hamiltonian Monte Carlo for Gaussian Process Models

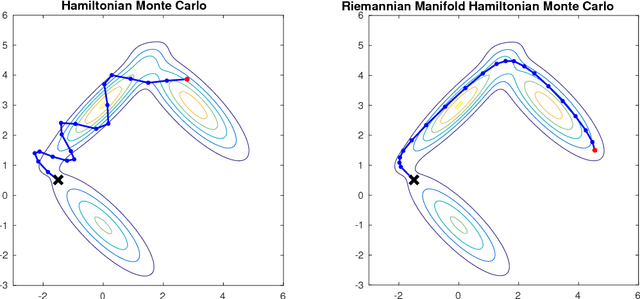
This technical report presents pseudo-code for a Riemannian manifold Hamiltonian Monte Carlo (RMHMC) method to efficiently simulate samples from $N$-dimensional posterior distributions $p(x|y)$, where $x \in R^N$ is drawn from a Gaussian Process (GP) prior, and observations $y_n$ are independent given $x_n$. Sufficient technical and algorithmic details are provided for the implementation of RMHMC for distributions arising from GP priors.

Generative Temporal Models with Spatial Memory for Partially Observed Environments

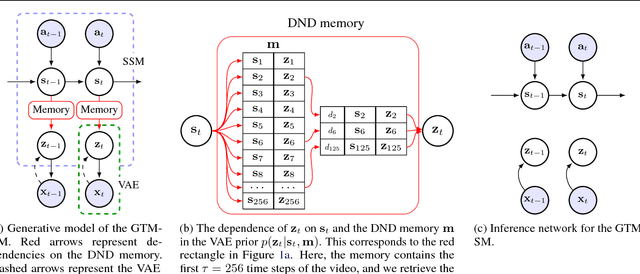
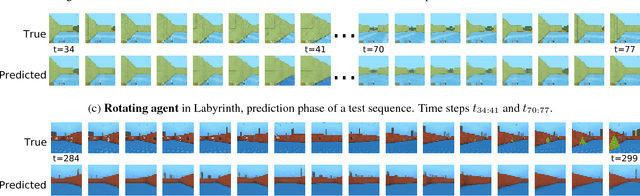
In model-based reinforcement learning, generative and temporal models of environments can be leveraged to boost agent performance, either by tuning the agent's representations during training or via use as part of an explicit planning mechanism. However, their application in practice has been limited to simplistic environments, due to the difficulty of training such models in larger, potentially partially-observed and 3D environments. In this work we introduce a novel action-conditioned generative model of such challenging environments. The model features a non-parametric spatial memory system in which we store learned, disentangled representations of the environment. Low-dimensional spatial updates are computed using a state-space model that makes use of knowledge on the prior dynamics of the moving agent, and high-dimensional visual observations are modelled with a Variational Auto-Encoder. The result is a scalable architecture capable of performing coherent predictions over hundreds of time steps across a range of partially observed 2D and 3D environments.

A Disentangled Recognition and Nonlinear Dynamics Model for Unsupervised Learning

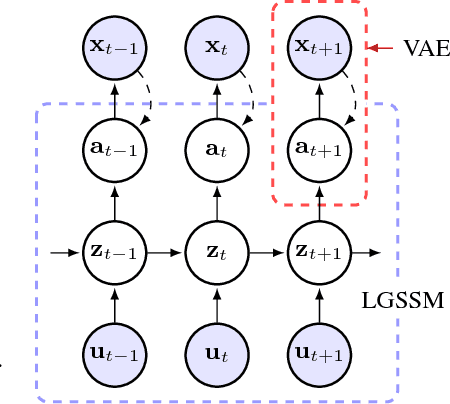
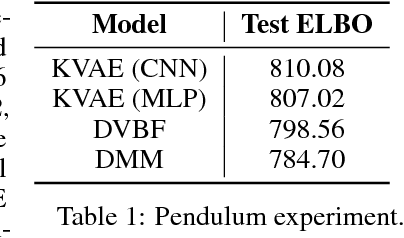
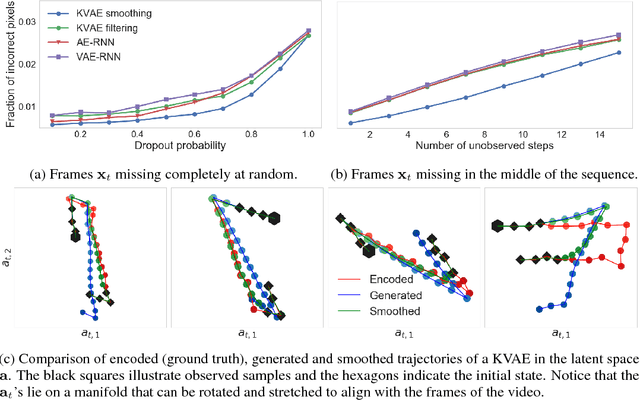
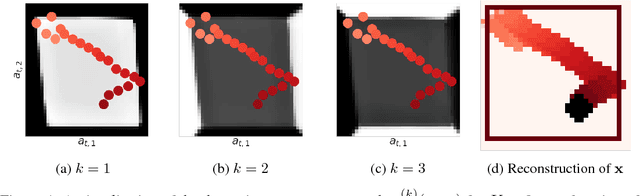
This paper takes a step towards temporal reasoning in a dynamically changing video, not in the pixel space that constitutes its frames, but in a latent space that describes the non-linear dynamics of the objects in its world. We introduce the Kalman variational auto-encoder, a framework for unsupervised learning of sequential data that disentangles two latent representations: an object's representation, coming from a recognition model, and a latent state describing its dynamics. As a result, the evolution of the world can be imagined and missing data imputed, both without the need to generate high dimensional frames at each time step. The model is trained end-to-end on videos of a variety of simulated physical systems, and outperforms competing methods in generative and missing data imputation tasks.

Semi-Supervised Generation with Cluster-aware Generative Models

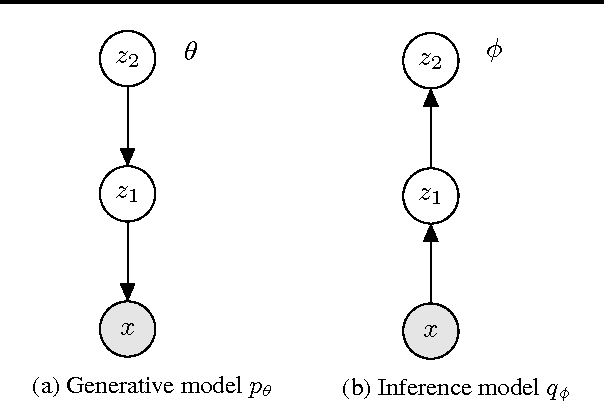
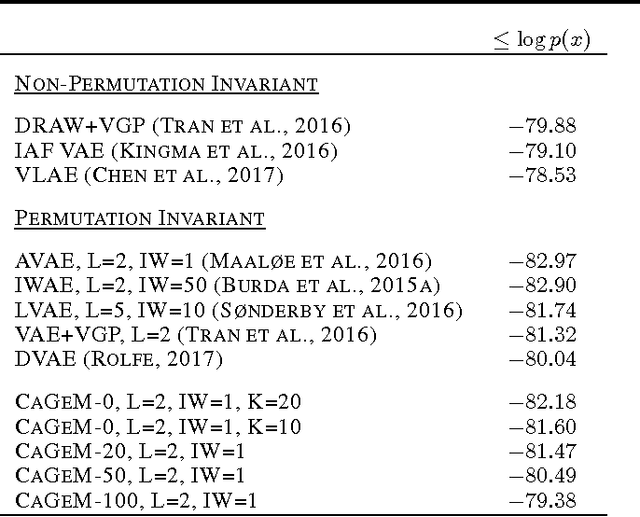
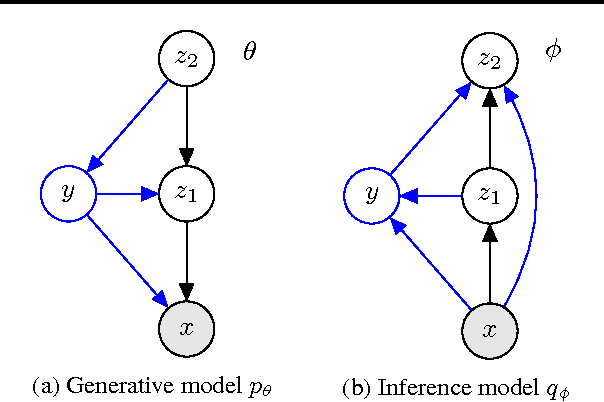
Deep generative models trained with large amounts of unlabelled data have proven to be powerful within the domain of unsupervised learning. Many real life data sets contain a small amount of labelled data points, that are typically disregarded when training generative models. We propose the Cluster-aware Generative Model, that uses unlabelled information to infer a latent representation that models the natural clustering of the data, and additional labelled data points to refine this clustering. The generative performances of the model significantly improve when labelled information is exploited, obtaining a log-likelihood of -79.38 nats on permutation invariant MNIST, while also achieving competitive semi-supervised classification accuracies. The model can also be trained fully unsupervised, and still improve the log-likelihood performance with respect to related methods.

Sequential Neural Models with Stochastic Layers

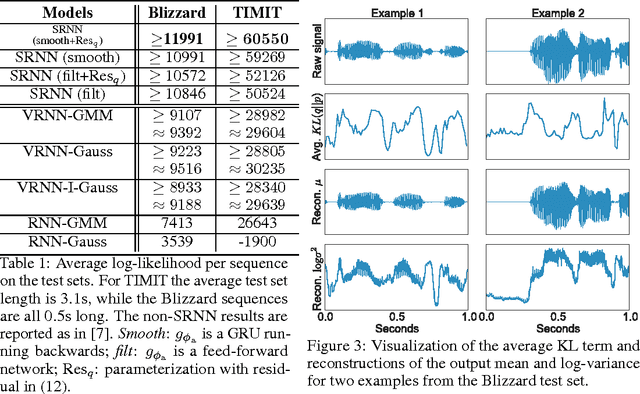
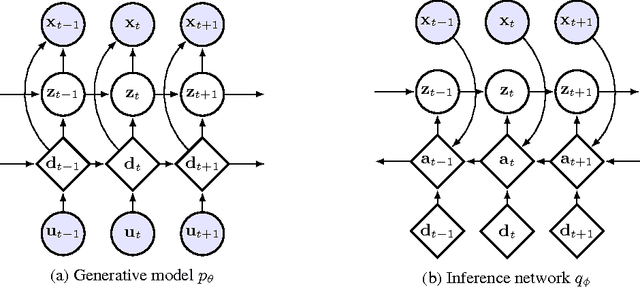
How can we efficiently propagate uncertainty in a latent state representation with recurrent neural networks? This paper introduces stochastic recurrent neural networks which glue a deterministic recurrent neural network and a state space model together to form a stochastic and sequential neural generative model. The clear separation of deterministic and stochastic layers allows a structured variational inference network to track the factorization of the model's posterior distribution. By retaining both the nonlinear recursive structure of a recurrent neural network and averaging over the uncertainty in a latent path, like a state space model, we improve the state of the art results on the Blizzard and TIMIT speech modeling data sets by a large margin, while achieving comparable performances to competing methods on polyphonic music modeling.

An Adaptive Resample-Move Algorithm for Estimating Normalizing Constants

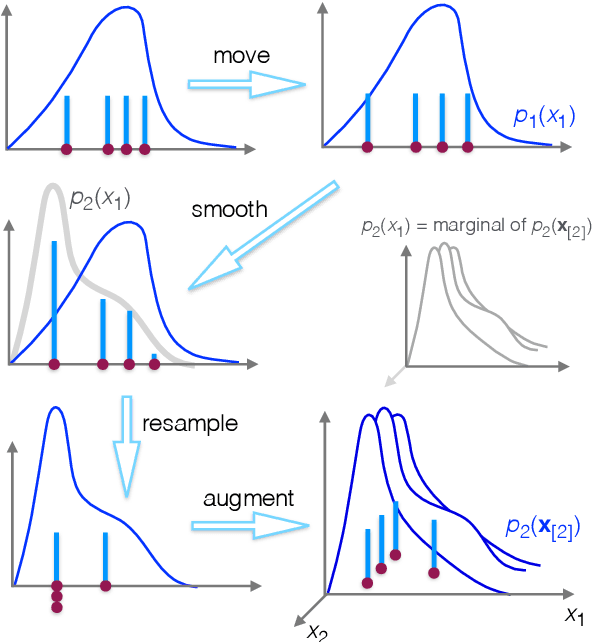
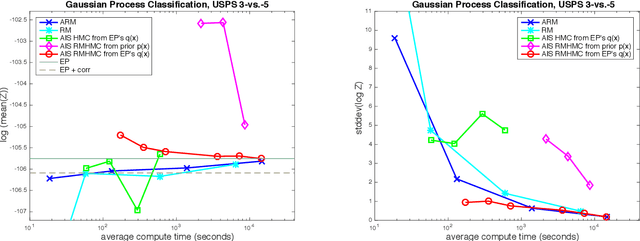
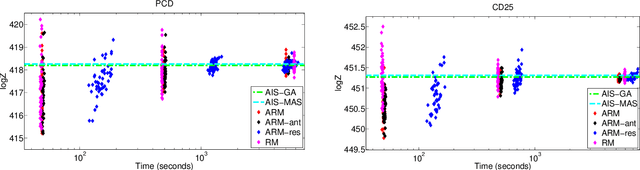
The estimation of normalizing constants is a fundamental step in probabilistic model comparison. Sequential Monte Carlo methods may be used for this task and have the advantage of being inherently parallelizable. However, the standard choice of using a fixed number of particles at each iteration is suboptimal because some steps will contribute disproportionately to the variance of the estimate. We introduce an adaptive version of the Resample-Move algorithm, in which the particle set is adaptively expanded whenever a better approximation of an intermediate distribution is needed. The algorithm builds on the expression for the optimal number of particles and the corresponding minimum variance found under ideal conditions. Benchmark results on challenging Gaussian Process Classification and Restricted Boltzmann Machine applications show that Adaptive Resample-Move (ARM) estimates the normalizing constant with a smaller variance, using less computational resources, than either Resample-Move with a fixed number of particles or Annealed Importance Sampling. A further advantage over Annealed Importance Sampling is that ARM is easier to tune.