The Sample Complexity of Learning Linear Predictors with the Squared Loss

In this short note, we provide tight sample complexity bounds for learning linear predictors with respect to the squared loss. Our focus is on an agnostic setting, where no assumptions are made on the data distribution. This contrasts with standard results in the literature, which either make distributional assumptions, refer to specific parameter settings, or use other performance measures.

Graph Approximation and Clustering on a Budget

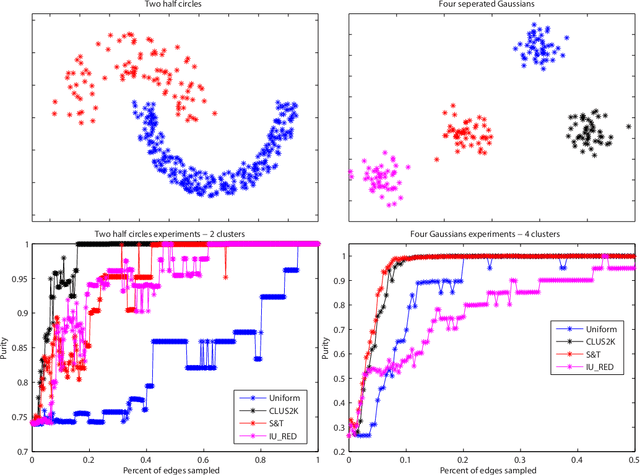
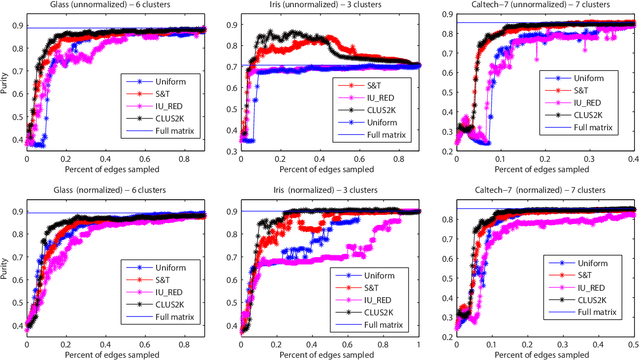
We consider the problem of learning from a similarity matrix (such as spectral clustering and lowd imensional embedding), when computing pairwise similarities are costly, and only a limited number of entries can be observed. We provide a theoretical analysis using standard notions of graph approximation, significantly generalizing previous results (which focused on spectral clustering with two clusters). We also propose a new algorithmic approach based on adaptive sampling, which experimentally matches or improves on previous methods, while being considerably more general and computationally cheaper.

Communication Efficient Distributed Optimization using an Approximate Newton-type Method

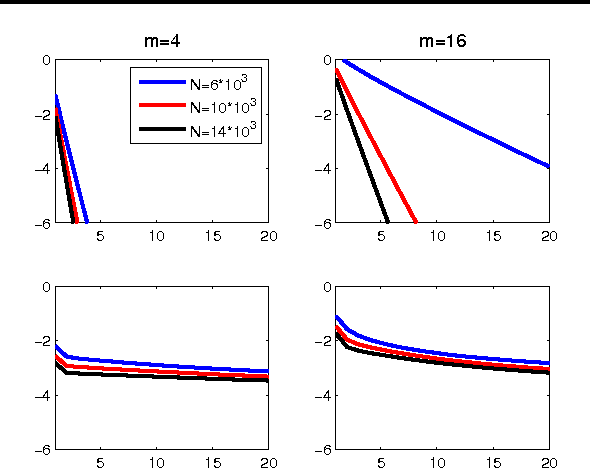
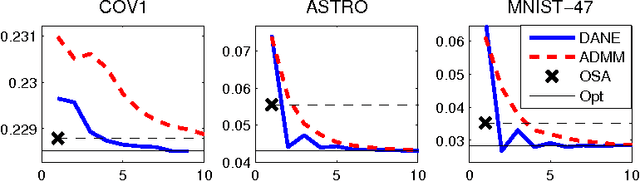
We present a novel Newton-type method for distributed optimization, which is particularly well suited for stochastic optimization and learning problems. For quadratic objectives, the method enjoys a linear rate of convergence which provably \emph{improves} with the data size, requiring an essentially constant number of iterations under reasonable assumptions. We provide theoretical and empirical evidence of the advantages of our method compared to other approaches, such as one-shot parameter averaging and ADMM.

An Algorithm for Training Polynomial Networks

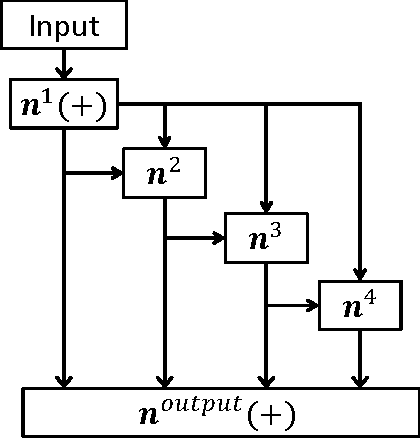
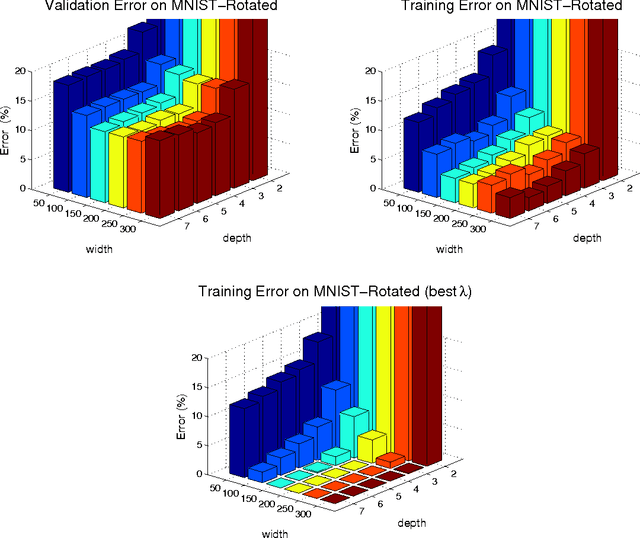
We consider deep neural networks, in which the output of each node is a quadratic function of its inputs. Similar to other deep architectures, these networks can compactly represent any function on a finite training set. The main goal of this paper is the derivation of an efficient layer-by-layer algorithm for training such networks, which we denote as the \emph{Basis Learner}. The algorithm is a universal learner in the sense that the training error is guaranteed to decrease at every iteration, and can eventually reach zero under mild conditions. We present practical implementations of this algorithm, as well as preliminary experimental results. We also compare our deep architecture to other shallow architectures for learning polynomials, in particular kernel learning.

Efficient Transductive Online Learning via Randomized Rounding

Most traditional online learning algorithms are based on variants of mirror descent or follow-the-leader. In this paper, we present an online algorithm based on a completely different approach, tailored for transductive settings, which combines "random playout" and randomized rounding of loss subgradients. As an application of our approach, we present the first computationally efficient online algorithm for collaborative filtering with trace-norm constrained matrices. As a second application, we solve an open question linking batch learning and transductive online learning

Online Learning with Switching Costs and Other Adaptive Adversaries

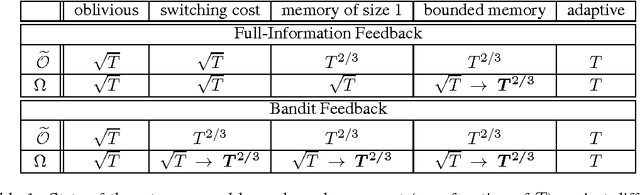
We study the power of different types of adaptive (nonoblivious) adversaries in the setting of prediction with expert advice, under both full-information and bandit feedback. We measure the player's performance using a new notion of regret, also known as policy regret, which better captures the adversary's adaptiveness to the player's behavior. In a setting where losses are allowed to drift, we characterize ---in a nearly complete manner--- the power of adaptive adversaries with bounded memories and switching costs. In particular, we show that with switching costs, the attainable rate with bandit feedback is $\widetilde{\Theta}(T^{2/3})$. Interestingly, this rate is significantly worse than the $\Theta(\sqrt{T})$ rate attainable with switching costs in the full-information case. Via a novel reduction from experts to bandits, we also show that a bounded memory adversary can force $\widetilde{\Theta}(T^{2/3})$ regret even in the full information case, proving that switching costs are easier to control than bounded memory adversaries. Our lower bounds rely on a new stochastic adversary strategy that generates loss processes with strong dependencies.

On the Complexity of Bandit and Derivative-Free Stochastic Convex Optimization

The problem of stochastic convex optimization with bandit feedback (in the learning community) or without knowledge of gradients (in the optimization community) has received much attention in recent years, in the form of algorithms and performance upper bounds. However, much less is known about the inherent complexity of these problems, and there are few lower bounds in the literature, especially for nonlinear functions. In this paper, we investigate the attainable error/regret in the bandit and derivative-free settings, as a function of the dimension d and the available number of queries T. We provide a precise characterization of the attainable performance for strongly-convex and smooth functions, which also imply a non-trivial lower bound for more general problems. Moreover, we prove that in both the bandit and derivative-free setting, the required number of queries must scale at least quadratically with the dimension. Finally, we show that on the natural class of quadratic functions, it is possible to obtain a "fast" O(1/T) error rate in terms of T, under mild assumptions, even without having access to gradients. To the best of our knowledge, this is the first such rate in a derivative-free stochastic setting, and holds despite previous results which seem to imply the contrary.

Online Learning for Time Series Prediction

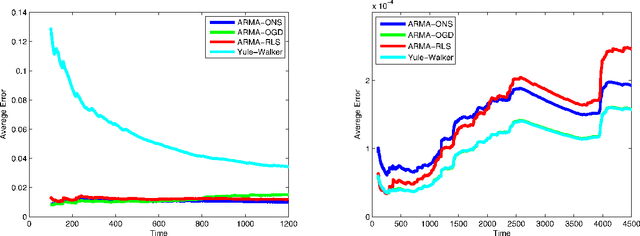
In this paper we address the problem of predicting a time series using the ARMA (autoregressive moving average) model, under minimal assumptions on the noise terms. Using regret minimization techniques, we develop effective online learning algorithms for the prediction problem, without assuming that the noise terms are Gaussian, identically distributed or even independent. Furthermore, we show that our algorithm's performances asymptotically approaches the performance of the best ARMA model in hindsight.

Stochastic Gradient Descent for Non-smooth Optimization: Convergence Results and Optimal Averaging Schemes

Stochastic Gradient Descent (SGD) is one of the simplest and most popular stochastic optimization methods. While it has already been theoretically studied for decades, the classical analysis usually required non-trivial smoothness assumptions, which do not apply to many modern applications of SGD with non-smooth objective functions such as support vector machines. In this paper, we investigate the performance of SGD without such smoothness assumptions, as well as a running average scheme to convert the SGD iterates to a solution with optimal optimization accuracy. In this framework, we prove that after T rounds, the suboptimality of the last SGD iterate scales as O(log(T)/\sqrt{T}) for non-smooth convex objective functions, and O(log(T)/T) in the non-smooth strongly convex case. To the best of our knowledge, these are the first bounds of this kind, and almost match the minimax-optimal rates obtainable by appropriate averaging schemes. We also propose a new and simple averaging scheme, which not only attains optimal rates, but can also be easily computed on-the-fly (in contrast, the suffix averaging scheme proposed in Rakhlin et al. (2011) is not as simple to implement). Finally, we provide some experimental illustrations.

Making Gradient Descent Optimal for Strongly Convex Stochastic Optimization

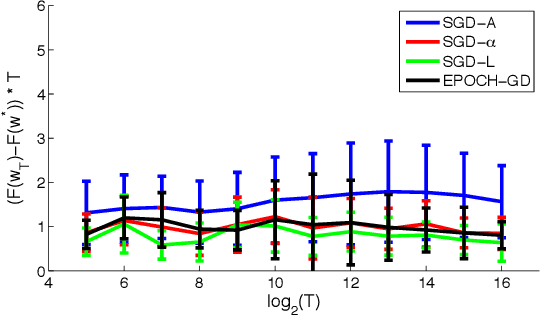
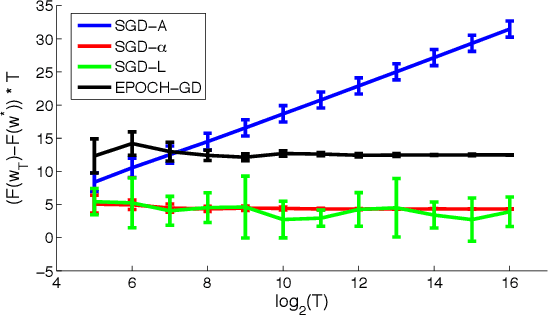
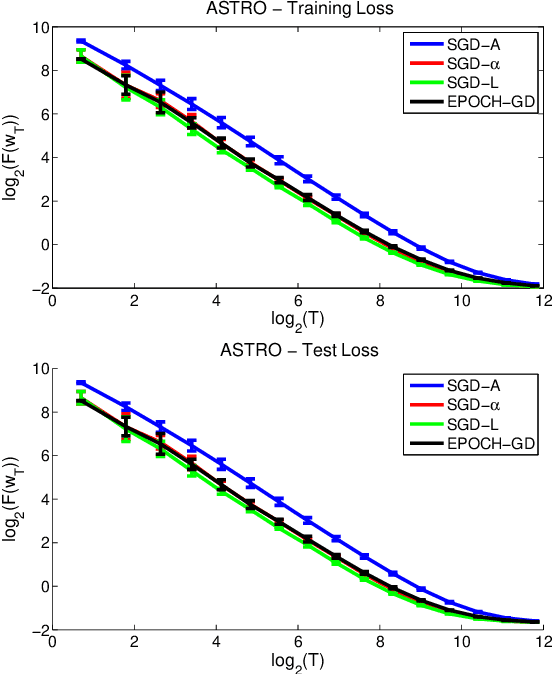
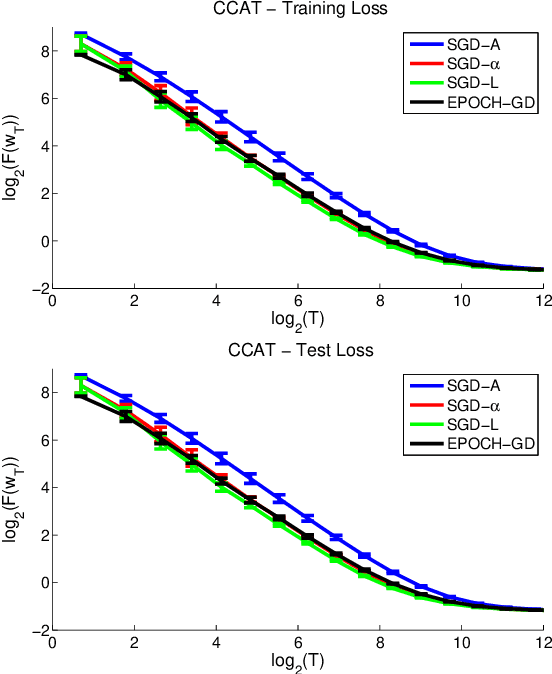
Stochastic gradient descent (SGD) is a simple and popular method to solve stochastic optimization problems which arise in machine learning. For strongly convex problems, its convergence rate was known to be O(\log(T)/T), by running SGD for T iterations and returning the average point. However, recent results showed that using a different algorithm, one can get an optimal O(1/T) rate. This might lead one to believe that standard SGD is suboptimal, and maybe should even be replaced as a method of choice. In this paper, we investigate the optimality of SGD in a stochastic setting. We show that for smooth problems, the algorithm attains the optimal O(1/T) rate. However, for non-smooth problems, the convergence rate with averaging might really be \Omega(\log(T)/T), and this is not just an artifact of the analysis. On the flip side, we show that a simple modification of the averaging step suffices to recover the O(1/T) rate, and no other change of the algorithm is necessary. We also present experimental results which support our findings, and point out open problems.