Ohad Shamir
Exponential Convergence Time of Gradient Descent for One-Dimensional Deep Linear Neural Networks
Sep 27, 2018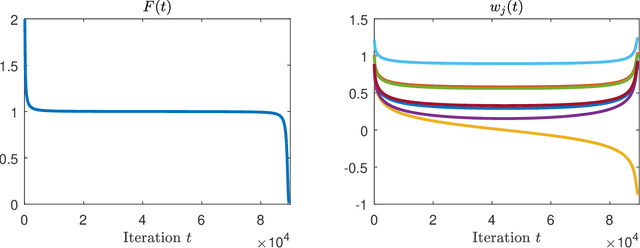
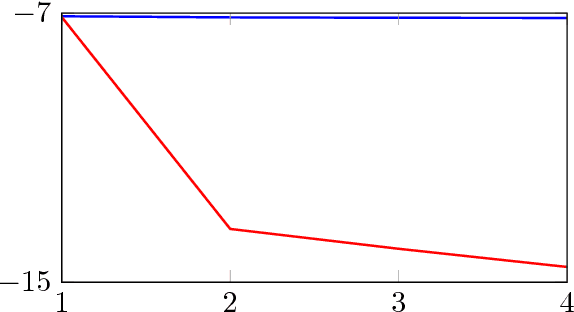
Abstract:In this note, we study the dynamics of gradient descent on objective functions of the form $f(\prod_{i=1}^{k} w_i)$ (with respect to scalar parameters $w_1,\ldots,w_k$), which arise in the context of training depth-$k$ linear neural networks. We prove that for standard random initializations, and under mild assumptions on $f$, the number of iterations required for convergence scales exponentially with the depth $k$. This highlights a potential obstacle in understanding the convergence of gradient-based methods for deep linear neural networks, where $k$ is large.
Spurious Local Minima are Common in Two-Layer ReLU Neural Networks
Aug 09, 2018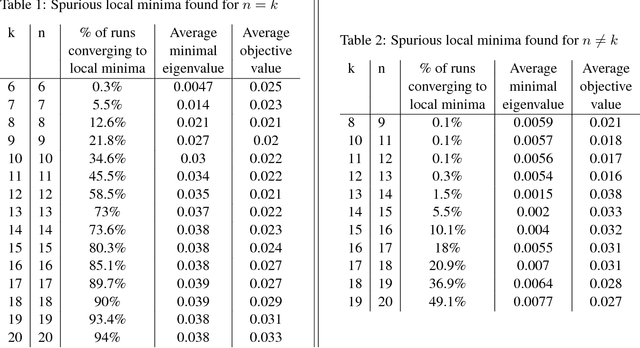
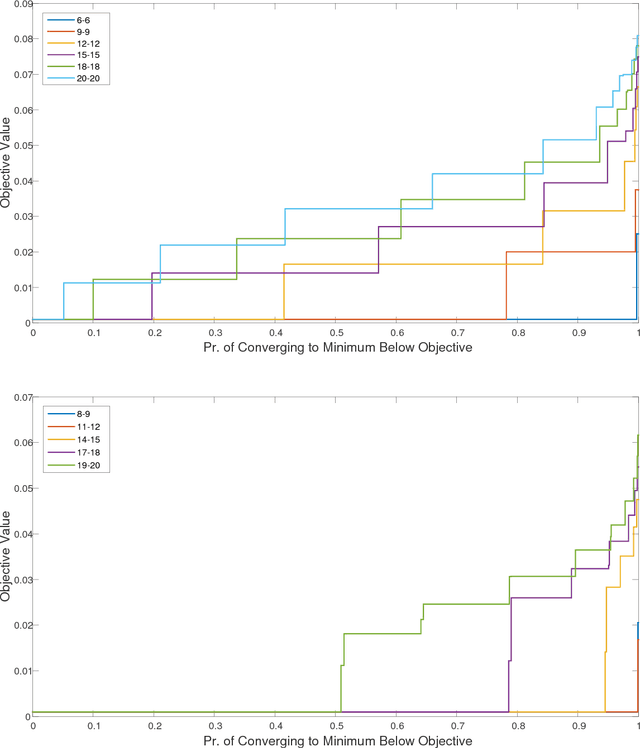
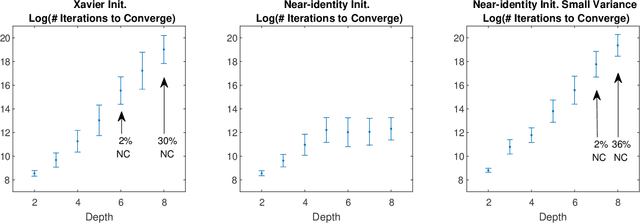
Abstract:We consider the optimization problem associated with training simple ReLU neural networks of the form $\mathbf{x}\mapsto \sum_{i=1}^{k}\max\{0,\mathbf{w}_i^\top \mathbf{x}\}$ with respect to the squared loss. We provide a computer-assisted proof that even if the input distribution is standard Gaussian, even if the dimension is arbitrarily large, and even if the target values are generated by such a network, with orthonormal parameter vectors, the problem can still have spurious local minima once $6\le k\le 20$. By a concentration of measure argument, this implies that in high input dimensions, \emph{nearly all} target networks of the relevant sizes lead to spurious local minima. Moreover, we conduct experiments which show that the probability of hitting such local minima is quite high, and increasing with the network size. On the positive side, mild over-parameterization appears to drastically reduce such local minima, indicating that an over-parameterization assumption is necessary to get a positive result in this setting.
A Tight Convergence Analysis for Stochastic Gradient Descent with Delayed Updates
Jun 26, 2018Abstract:We provide tight finite-time convergence bounds for gradient descent and stochastic gradient descent on quadratic functions, when the gradients are delayed and reflect iterates from $\tau$ rounds ago. First, we show that without stochastic noise, delays strongly affect the attainable optimization error: In fact, the error can be as bad as non-delayed gradient descent ran on only $1/\tau$ of the gradients. In sharp contrast, we quantify how stochastic noise makes the effect of delays negligible, improving on previous work which only showed this phenomenon asymptotically or for much smaller delays. Also, in the context of distributed optimization, the results indicate that the performance of gradient descent with delays is competitive with synchronous approaches such as mini-batching. Our results are based on a novel technique for analyzing convergence of optimization algorithms using generating functions.
Detecting Correlations with Little Memory and Communication
Jun 06, 2018Abstract:We study the problem of identifying correlations in multivariate data, under information constraints: Either on the amount of memory that can be used by the algorithm, or the amount of communication when the data is distributed across several machines. We prove a tight trade-off between the memory/communication complexity and the sample complexity, implying (for example) that to detect pairwise correlations with optimal sample complexity, the number of required memory/communication bits is at least quadratic in the dimension. Our results substantially improve those of Shamir [2014], which studied a similar question in a much more restricted setting. To the best of our knowledge, these are the first provable sample/memory/communication trade-offs for a practical estimation problem, using standard distributions, and in the natural regime where the memory/communication budget is larger than the size of a single data point. To derive our theorems, we prove a new information-theoretic result, which may be relevant for studying other information-constrained learning problems.
Size-Independent Sample Complexity of Neural Networks
Jun 06, 2018Abstract:We study the sample complexity of learning neural networks, by providing new bounds on their Rademacher complexity assuming norm constraints on the parameter matrix of each layer. Compared to previous work, these complexity bounds have improved dependence on the network depth, and under some additional assumptions, are fully independent of the network size (both depth and width). These results are derived using some novel techniques, which may be of independent interest.
Weight Sharing is Crucial to Succesful Optimization
Jun 02, 2017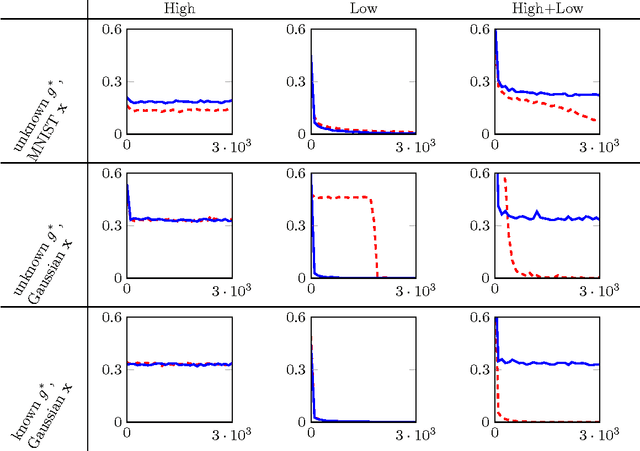
Abstract:Exploiting the great expressive power of Deep Neural Network architectures, relies on the ability to train them. While current theoretical work provides, mostly, results showing the hardness of this task, empirical evidence usually differs from this line, with success stories in abundance. A strong position among empirically successful architectures is captured by networks where extensive weight sharing is used, either by Convolutional or Recurrent layers. Additionally, characterizing specific aspects of different tasks, making them "harder" or "easier", is an interesting direction explored both theoretically and empirically. We consider a family of ConvNet architectures, and prove that weight sharing can be crucial, from an optimization point of view. We explore different notions of the frequency, of the target function, proving necessity of the target function having some low frequency components. This necessity is not sufficient - only with weight sharing can it be exploited, thus theoretically separating architectures using it, from others which do not. Our theoretical results are aligned with empirical experiments in an even more general setting, suggesting viability of examination of the role played by interleaving those aspects in broader families of tasks.
Bandit Regret Scaling with the Effective Loss Range
May 18, 2017Abstract:We study how the regret guarantees of nonstochastic multi-armed bandits can be improved, if the effective range of the losses in each round is small (e.g. the maximal difference between two losses in a given round). Despite a recent impossibility result, we show how this can be made possible under certain mild additional assumptions, such as availability of rough estimates of the losses, or advance knowledge of the loss of a single, possibly unspecified arm. Along the way, we develop a novel technique which might be of independent interest, to convert any multi-armed bandit algorithm with regret depending on the loss range, to an algorithm with regret depending only on the effective range, while avoiding predictably bad arms altogether.
Failures of Gradient-Based Deep Learning
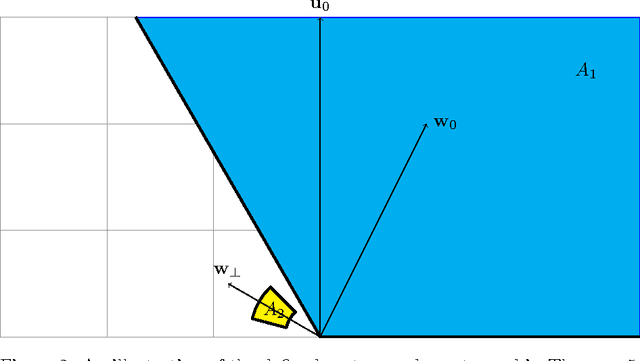
Apr 26, 2017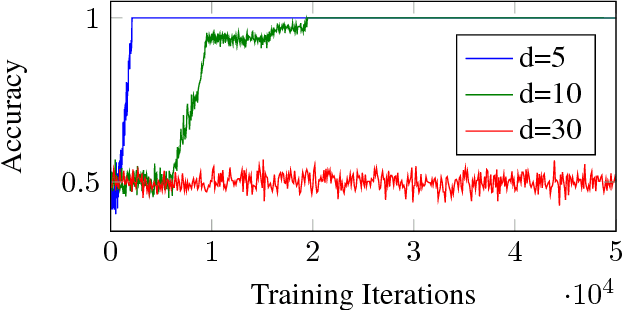

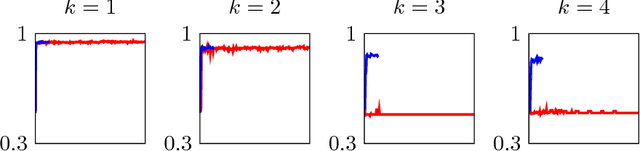
Abstract:In recent years, Deep Learning has become the go-to solution for a broad range of applications, often outperforming state-of-the-art. However, it is important, for both theoreticians and practitioners, to gain a deeper understanding of the difficulties and limitations associated with common approaches and algorithms. We describe four types of simple problems, for which the gradient-based algorithms commonly used in deep learning either fail or suffer from significant difficulties. We illustrate the failures through practical experiments, and provide theoretical insights explaining their source, and how they might be remedied.
Online Learning with Local Permutations and Delayed Feedback
Mar 13, 2017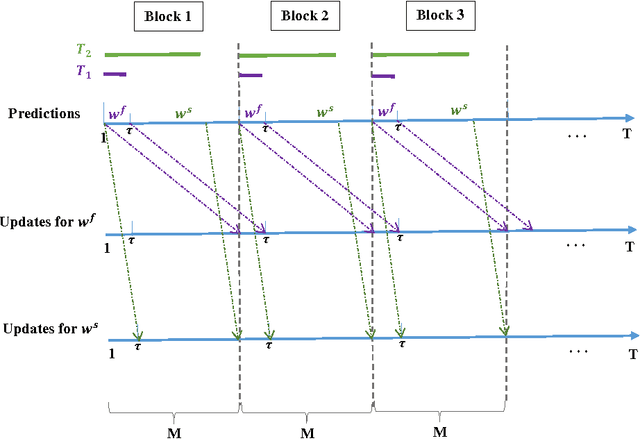
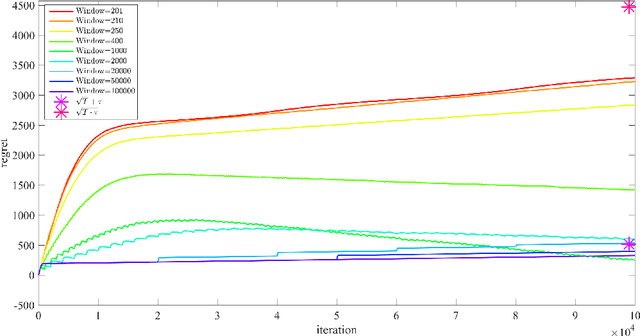
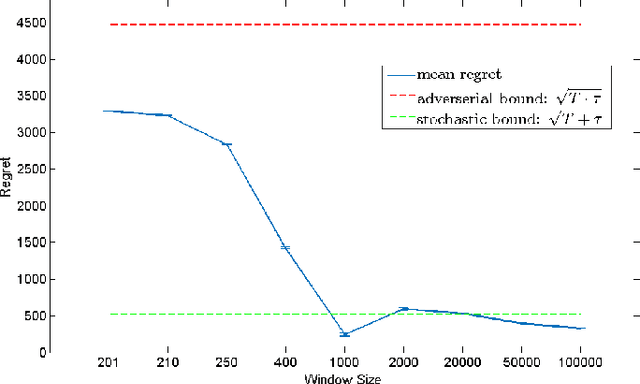
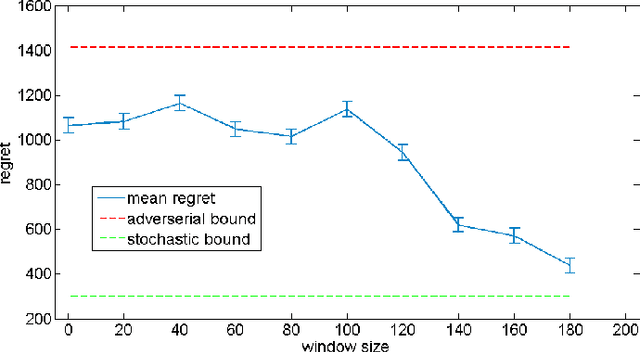
Abstract:We propose an Online Learning with Local Permutations (OLLP) setting, in which the learner is allowed to slightly permute the \emph{order} of the loss functions generated by an adversary. On one hand, this models natural situations where the exact order of the learner's responses is not crucial, and on the other hand, might allow better learning and regret performance, by mitigating highly adversarial loss sequences. Also, with random permutations, this can be seen as a setting interpolating between adversarial and stochastic losses. In this paper, we consider the applicability of this setting to convex online learning with delayed feedback, in which the feedback on the prediction made in round $t$ arrives with some delay $\tau$. With such delayed feedback, the best possible regret bound is well-known to be $O(\sqrt{\tau T})$. We prove that by being able to permute losses by a distance of at most $M$ (for $M\geq \tau$), the regret can be improved to $O(\sqrt{T}(1+\sqrt{\tau^2/M}))$, using a Mirror-Descent based algorithm which can be applied for both Euclidean and non-Euclidean geometries. We also prove a lower bound, showing that for $M<\tau/3$, it is impossible to improve the standard $O(\sqrt{\tau T})$ regret bound by more than constant factors. Finally, we provide some experiments validating the performance of our algorithm.
Depth-Width Tradeoffs in Approximating Natural Functions with Neural Networks
Mar 09, 2017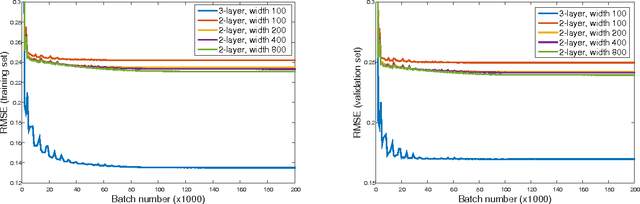
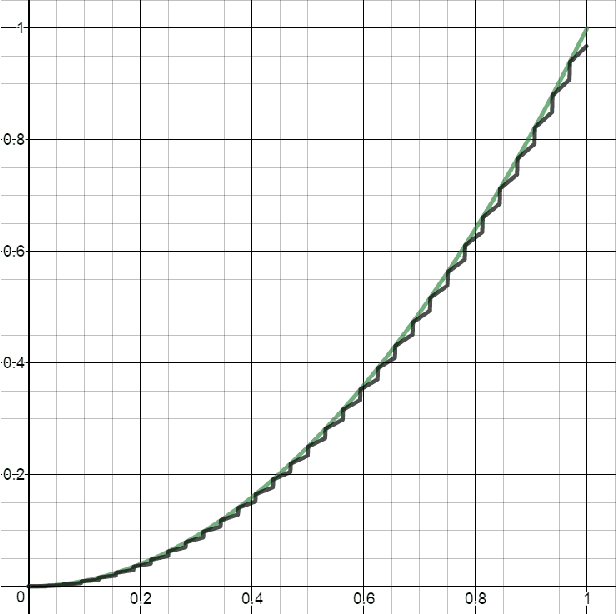
Abstract:We provide several new depth-based separation results for feed-forward neural networks, proving that various types of simple and natural functions can be better approximated using deeper networks than shallower ones, even if the shallower networks are much larger. This includes indicators of balls and ellipses; non-linear functions which are radial with respect to the $L_1$ norm; and smooth non-linear functions. We also show that these gaps can be observed experimentally: Increasing the depth indeed allows better learning than increasing width, when training neural networks to learn an indicator of a unit ball.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge