Prospective Learning: Back to the Future

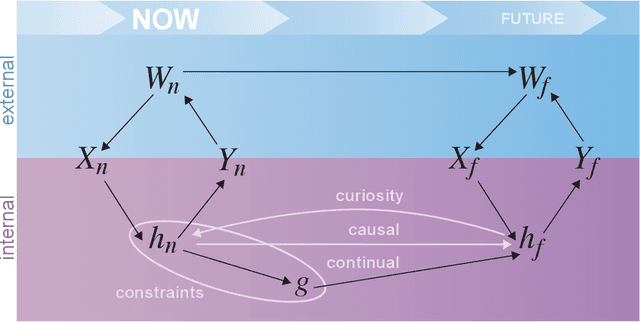
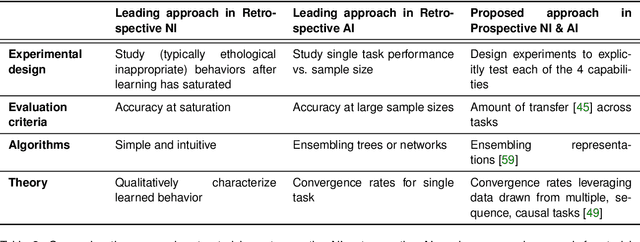
Research on both natural intelligence (NI) and artificial intelligence (AI) generally assumes that the future resembles the past: intelligent agents or systems (what we call 'intelligence') observe and act on the world, then use this experience to act on future experiences of the same kind. We call this 'retrospective learning'. For example, an intelligence may see a set of pictures of objects, along with their names, and learn to name them. A retrospective learning intelligence would merely be able to name more pictures of the same objects. We argue that this is not what true intelligence is about. In many real world problems, both NIs and AIs will have to learn for an uncertain future. Both must update their internal models to be useful for future tasks, such as naming fundamentally new objects and using these objects effectively in a new context or to achieve previously unencountered goals. This ability to learn for the future we call 'prospective learning'. We articulate four relevant factors that jointly define prospective learning. Continual learning enables intelligences to remember those aspects of the past which it believes will be most useful in the future. Prospective constraints (including biases and priors) facilitate the intelligence finding general solutions that will be applicable to future problems. Curiosity motivates taking actions that inform future decision making, including in previously unmet situations. Causal estimation enables learning the structure of relations that guide choosing actions for specific outcomes, even when the specific action-outcome contingencies have never been observed before. We argue that a paradigm shift from retrospective to prospective learning will enable the communities that study intelligence to unite and overcome existing bottlenecks to more effectively explain, augment, and engineer intelligences.

Dimensionality reduction, regularization, and generalization in overparameterized regressions

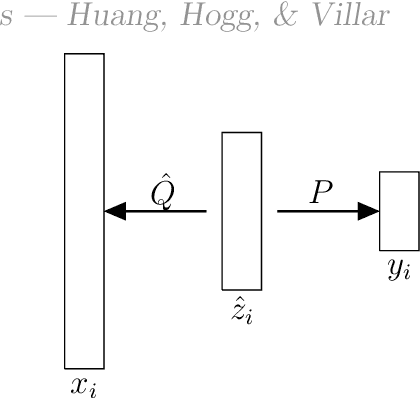
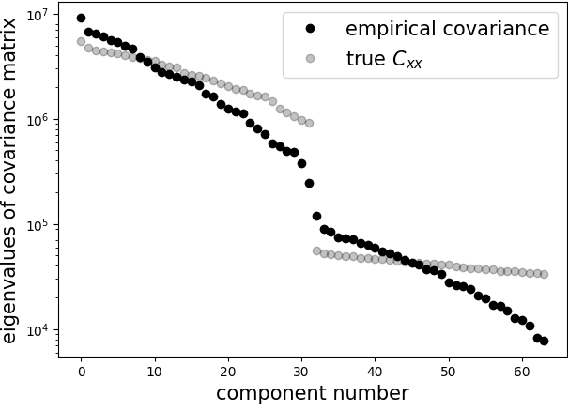
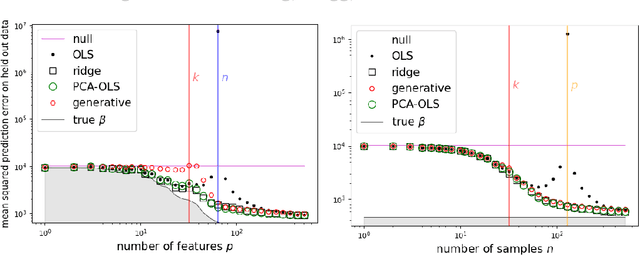
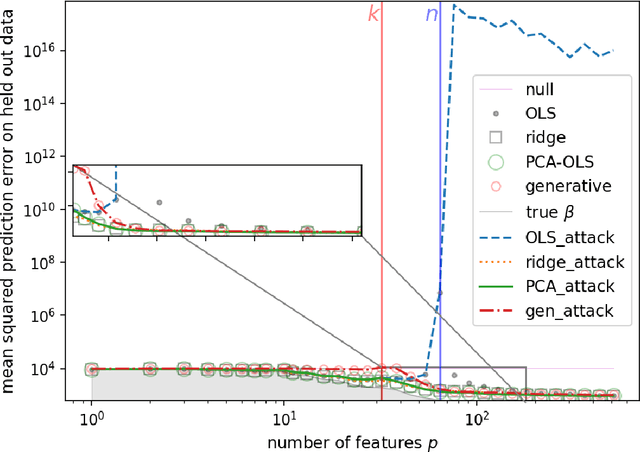
Overparameterization in deep learning is powerful: Very large models fit the training data perfectly and yet generalize well. This realization brought back the study of linear models for regression, including ordinary least squares (OLS), which, like deep learning, shows a "double descent" behavior. This involves two features: (1) The risk (out-of-sample prediction error) can grow arbitrarily when the number of samples $n$ approaches the number of parameters $p$, and (2) the risk decreases with $p$ at $p>n$, sometimes achieving a lower value than the lowest risk at $p<n$. The divergence of the risk for OLS at $p\approx n$ is related to the condition number of the empirical covariance in the feature set. For this reason, it can be avoided with regularization. In this work we show that it can also be avoided with a PCA-based dimensionality reduction. We provide a finite upper bound for the risk of the PCA-based estimator. This result is in contrast to recent work that shows that a different form of dimensionality reduction -- one based on the population covariance instead of the empirical covariance -- does not avoid the divergence. We connect these results to an analysis of adversarial attacks, which become more effective as they raise the condition number of the empirical covariance of the features. We show that OLS is arbitrarily susceptible to data-poisoning attacks in the overparameterized regime -- unlike the underparameterized regime -- and that regularization and dimensionality reduction improve the robustness.