Toroidal Probabilistic Spherical Discriminant Analysis

In speaker recognition, where speech segments are mapped to embeddings on the unit hypersphere, two scoring back-ends are commonly used, namely cosine scoring and PLDA. We have recently proposed PSDA, an analog to PLDA that uses Von Mises-Fisher distributions instead of Gaussians. In this paper, we present toroidal PSDA (T-PSDA). It extends PSDA with the ability to model within and between-speaker variabilities in toroidal submanifolds of the hypersphere. Like PLDA and PSDA, the model allows closed-form scoring and closed-form EM updates for training. On VoxCeleb, we find T-PSDA accuracy on par with cosine scoring, while PLDA accuracy is inferior. On NIST SRE'21 we find that T-PSDA gives large accuracy gains compared to both cosine scoring and PLDA.

Probabilistic Spherical Discriminant Analysis: An Alternative to PLDA for length-normalized embeddings

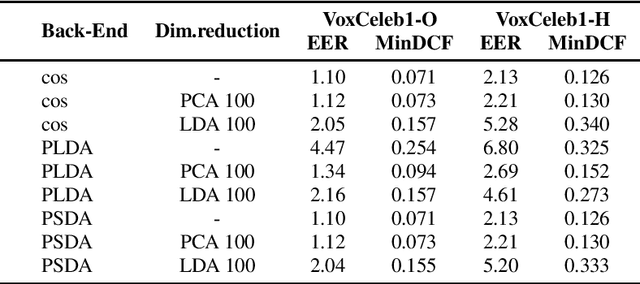
In speaker recognition, where speech segments are mapped to embeddings on the unit hypersphere, two scoring backends are commonly used, namely cosine scoring or PLDA. Both have advantages and disadvantages, depending on the context. Cosine scoring follows naturally from the spherical geometry, but for PLDA the blessing is mixed -- length normalization Gaussianizes the between-speaker distribution, but violates the assumption of a speaker-independent within-speaker distribution. We propose PSDA, an analogue to PLDA that uses Von Mises-Fisher distributions on the hypersphere for both within and between-class distributions. We show how the self-conjugacy of this distribution gives closed-form likelihood-ratio scores, making it a drop-in replacement for PLDA at scoring time. All kinds of trials can be scored, including single-enroll and multi-enroll verification, as well as more complex likelihood-ratios that could be used in clustering and diarization. Learning is done via an EM-algorithm with closed-form updates. We explain the model and present some first experiments.

How to use KL-divergence to construct conjugate priors, with well-defined non-informative limits, for the multivariate Gaussian

The Wishart distribution is the standard conjugate prior for the precision of the multivariate Gaussian likelihood, when the mean is known -- while the normal-Wishart can be used when the mean is also unknown. It is however not so obvious how to assign values to the hyperparameters of these distributions. In particular, when forming non-informative limits of these distributions, the shape (or degrees of freedom) parameter of the Wishart must be handled with care. The intuitive solution of directly interpreting the shape as a pseudocount and letting it go to zero, as proposed by some authors, violates the restrictions on the shape parameter. We show how to use the scaled KL-divergence between multivariate Gaussians as an energy function to construct Wishart and normal-Wishart conjugate priors. When used as informative priors, the salient feature of these distributions is the mode, while the KL scaling factor serves as the pseudocount. The scale factor can be taken down to the limit at zero, to form non-informative priors that do not violate the restrictions on the Wishart shape parameter. This limit is non-informative in the sense that the posterior mode is identical to the maximum likelihood estimate of the parameters of the Gaussian.

The Phonexia VoxCeleb Speaker Recognition Challenge 2021 System Description

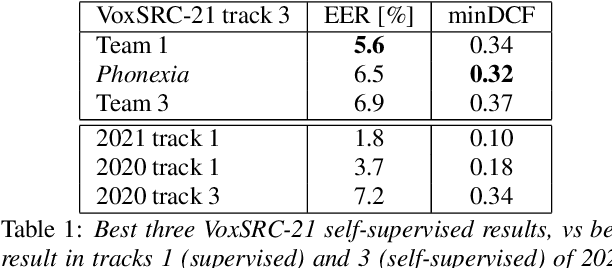
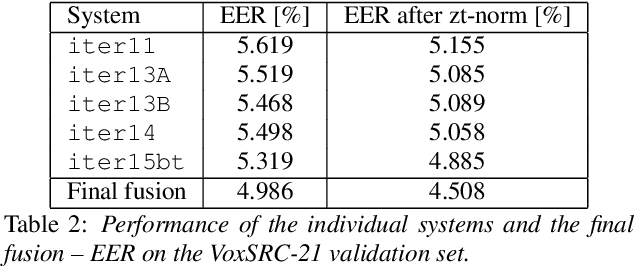
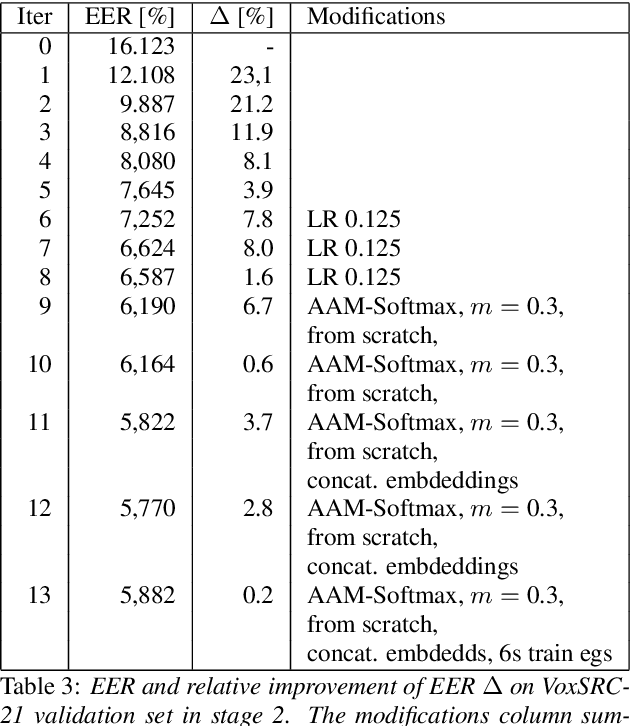
We describe the Phonexia submission for the VoxCeleb Speaker Recognition Challenge 2021 (VoxSRC-21) in the unsupervised speaker verification track. Our solution was very similar to IDLab's winning submission for VoxSRC-20. An embedding extractor was bootstrapped using momentum contrastive learning, with input augmentations as the only source of supervision. This was followed by several iterations of clustering to assign pseudo-speaker labels that were then used for supervised embedding extractor training. Finally, a score fusion was done, by averaging the zt-normalized cosine scores of five different embedding extractors. We briefly also describe unsuccessful solutions involving i-vectors instead of DNN embeddings and PLDA instead of cosine scoring.

Out of a hundred trials, how many errors does your speaker verifier make?

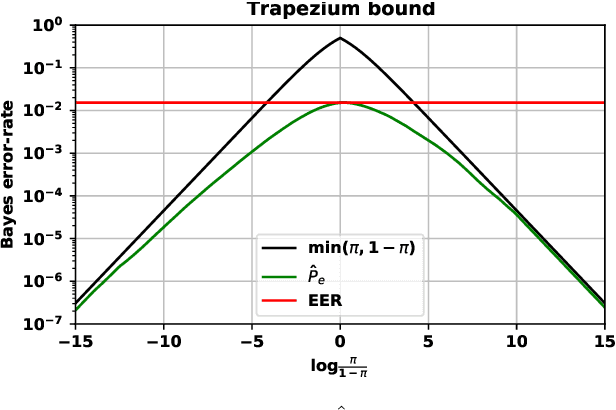
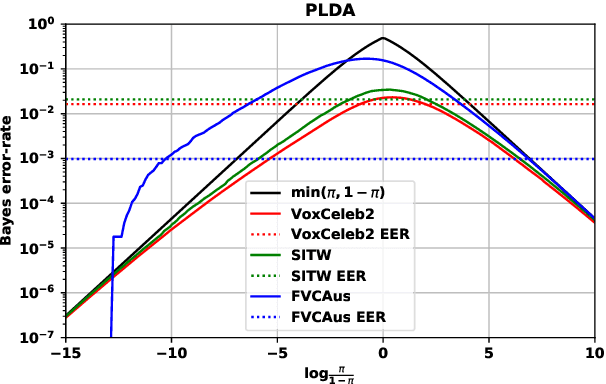
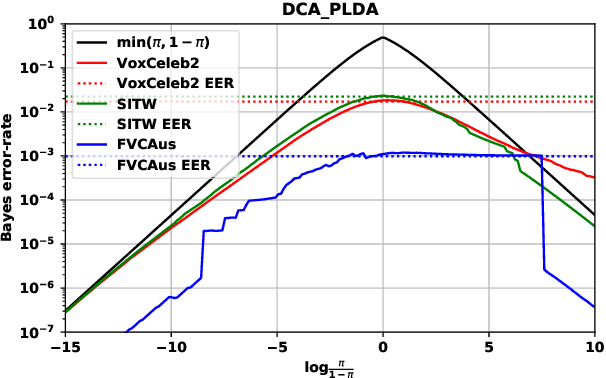
Out of a hundred trials, how many errors does your speaker verifier make? For the user this is an important, practical question, but researchers and vendors typically sidestep it and supply instead the conditional error-rates that are given by the ROC/DET curve. We posit that the user's question is answered by the Bayes error-rate. We present a tutorial to show how to compute the error-rate that results when making Bayes decisions with calibrated likelihood ratios, supplied by the verifier, and an hypothesis prior, supplied by the user. For perfect calibration, the Bayes error-rate is upper bounded by min(EER,P,1-P), where EER is the equal-error-rate and P, 1-P are the prior probabilities of the competing hypotheses. The EER represents the accuracy of the verifier, while min(P,1-P) represents the hardness of the classification problem. We further show how the Bayes error-rate can be computed also for non-perfect calibration and how to generalize from error-rate to expected cost. We offer some criticism of decisions made by direct score thresholding. Finally, we demonstrate by analyzing error-rates of the recently published DCA-PLDA speaker verifier.

Probabilistic embeddings for speaker diarization

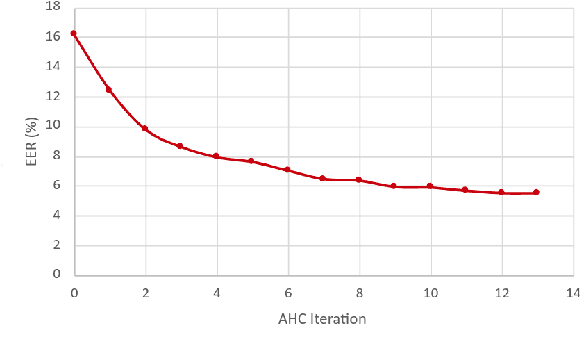
Speaker embeddings (x-vectors) extracted from very short segments of speech have recently been shown to give competitive performance in speaker diarization. We generalize this recipe by extracting from each speech segment, in parallel with the x-vector, also a diagonal precision matrix, thus providing a path for the propagation of information about the quality of the speech segment into a PLDA scoring backend. These precisions quantify the uncertainty about what the values of the embeddings might have been if they had been extracted from high quality speech segments. The proposed probabilistic embeddings (x-vectors with precisions) are interfaced with the PLDA model by treating the x-vectors as hidden variables and marginalizing them out. We apply the proposed probabilistic embeddings as input to an agglomerative hierarchical clustering (AHC) algorithm to do diarization in the DIHARD'19 evaluation set. We compute the full PLDA likelihood 'by the book' for each clustering hypothesis that is considered by AHC. We do joint discriminative training of the PLDA parameters and of the probabilistic x-vector extractor. We demonstrate accuracy gains relative to a baseline AHC algorithm, applied to traditional xvectors (without uncertainty), and which uses averaging of binary log-likelihood-ratios, rather than by-the-book scoring.

Language-depedent I-Vectors for LRE15

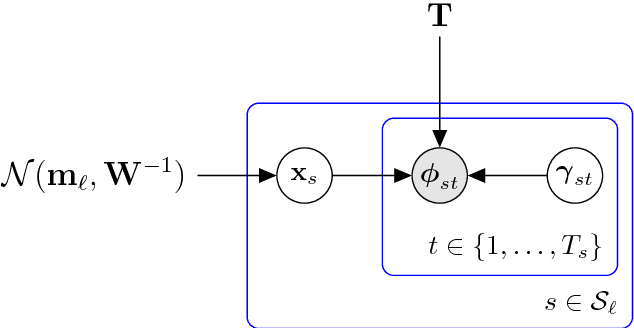
A standard recipe for spoken language recognition is to apply a Gaussian back-end to i-vectors. This ignores the uncertainty in the i-vector extraction, which could be important especially for short utterances. A recent paper by Cumani, Plchot and Fer proposes a solution to propagate that uncertainty into the backend. We propose an alternative method of propagating the uncertainty.

Note on the equivalence of hierarchical variational models and auxiliary deep generative models

This note compares two recently published machine learning methods for constructing flexible, but tractable families of variational hidden-variable posteriors. The first method, called "hierarchical variational models" enriches the inference model with an extra variable, while the other, called "auxiliary deep generative models", enriches the generative model instead. We conclude that the two methods are mathematically equivalent.

VB calibration to improve the interface between phone recognizer and i-vector extractor

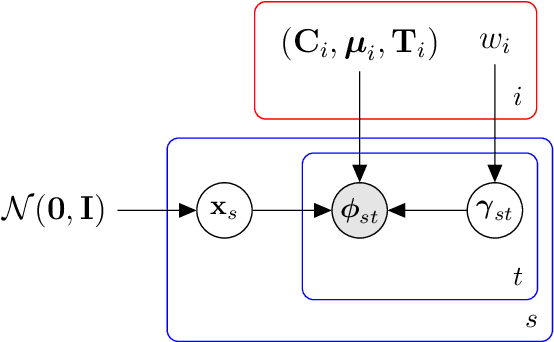
The EM training algorithm of the classical i-vector extractor is often incorrectly described as a maximum-likelihood method. The i-vector model is however intractable: the likelihood itself and the hidden-variable posteriors needed for the EM algorithm cannot be computed in closed form. We show here that the classical i-vector extractor recipe is actually a mean-field variational Bayes (VB) recipe. This theoretical VB interpretation turns out to be of further use, because it also offers an interpretation of the newer phonetic i-vector extractor recipe, thereby unifying the two flavours of extractor. More importantly, the VB interpretation is also practically useful: it suggests ways of modifying existing i-vector extractors to make them more accurate. In particular, in existing methods, the approximate VB posterior for the GMM states is fixed, while only the parameters of the generative model are adapted. Here we explore the possibility of also mildly adjusting (calibrating) those posteriors, so that they better fit the generative model.

Bayesian calibration for forensic evidence reporting

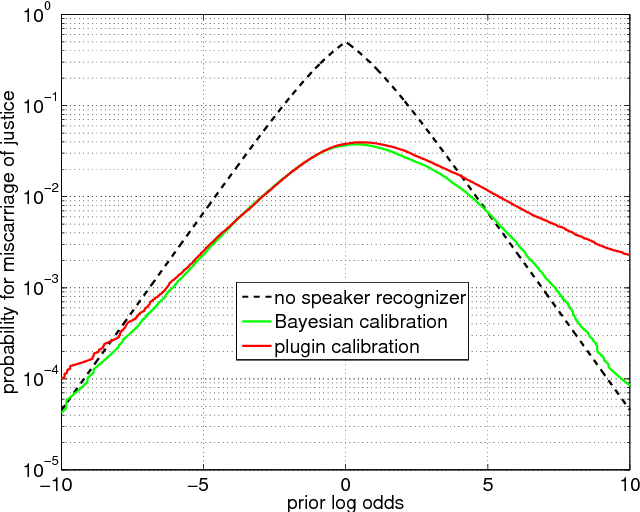
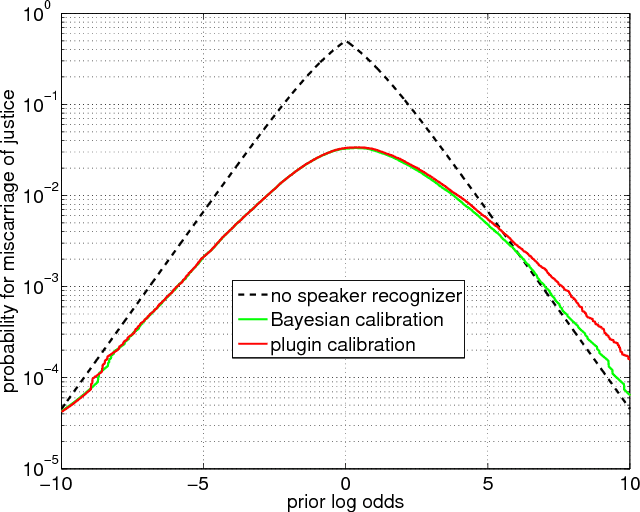
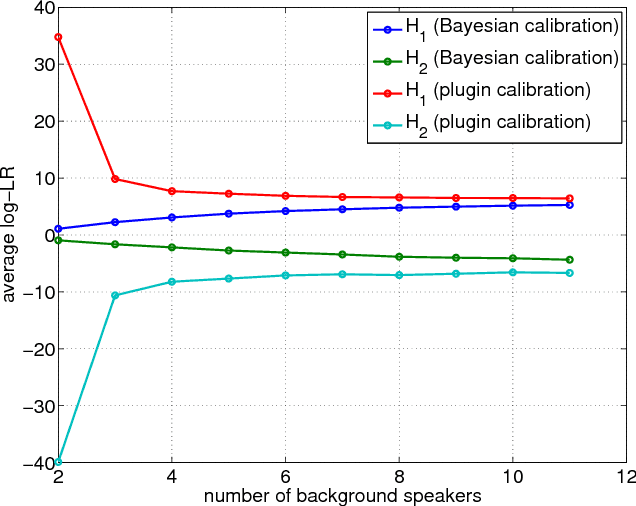
We introduce a Bayesian solution for the problem in forensic speaker recognition, where there may be very little background material for estimating score calibration parameters. We work within the Bayesian paradigm of evidence reporting and develop a principled probabilistic treatment of the problem, which results in a Bayesian likelihood-ratio as the vehicle for reporting weight of evidence. We show in contrast, that reporting a likelihood-ratio distribution does not solve this problem. Our solution is experimentally exercised on a simulated forensic scenario, using NIST SRE'12 scores, which demonstrates a clear advantage for the proposed method compared to the traditional plugin calibration recipe.