Exploring End-to-end Differentiable Neural Charged Particle Tracking -- A Loss Landscape Perspective

Measurement and analysis of high energetic particles for scientific, medical or industrial applications is a complex procedure, requiring the design of sophisticated detector and data processing systems. The development of adaptive and differentiable software pipelines using a combination of conventional and machine learning algorithms is therefore getting ever more important to optimize and operate the system efficiently while maintaining end-to-end (E2E) differentiability. We propose for the application of charged particle tracking an E2E differentiable decision-focused learning scheme using graph neural networks with combinatorial components solving a linear assignment problem for each detector layer. We demonstrate empirically that including differentiable variations of discrete assignment operations allows for efficient network optimization, working better or on par with approaches that lack E2E differentiability. In additional studies, we dive deeper into the optimization process and provide further insights from a loss landscape perspective. We demonstrate that while both methods converge into similar performing, globally well-connected regions, they suffer under substantial predictive instability across initialization and optimization methods, which can have unpredictable consequences on the performance of downstream tasks such as image reconstruction. We also point out a dependency between the interpolation factor of the gradient estimator and the prediction stability of the model, suggesting the choice of sufficiently small values. Given the strong global connectivity of learned solutions and the excellent training performance, we argue that E2E differentiability provides, besides the general availability of gradient information, an important tool for robust particle tracking to mitigate prediction instabilities by favoring solutions that perform well on downstream tasks.

Physics-Informed Learning of Aerosol Microphysics

Aerosol particles play an important role in the climate system by absorbing and scattering radiation and influencing cloud properties. They are also one of the biggest sources of uncertainty for climate modeling. Many climate models do not include aerosols in sufficient detail due to computational constraints. In order to represent key processes, aerosol microphysical properties and processes have to be accounted for. This is done in the ECHAM-HAM global climate aerosol model using the M7 microphysics, but high computational costs make it very expensive to run with finer resolution or for a longer time. We aim to use machine learning to emulate the microphysics model at sufficient accuracy and reduce the computational cost by being fast at inference time. The original M7 model is used to generate data of input-output pairs to train a neural network on it. We are able to learn the variables' tendencies achieving an average $R^2$ score of $77.1\% $. We further explore methods to inform and constrain the neural network with physical knowledge to reduce mass violation and enforce mass positivity. On a GPU we achieve a speed-up of up to over 64x compared to the original model.

Scalable Hyperparameter Optimization with Lazy Gaussian Processes

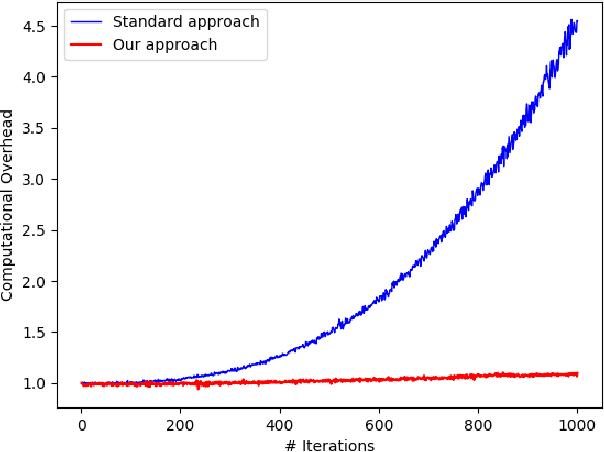
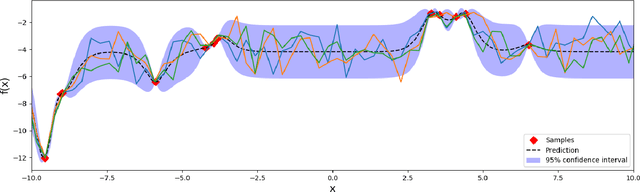
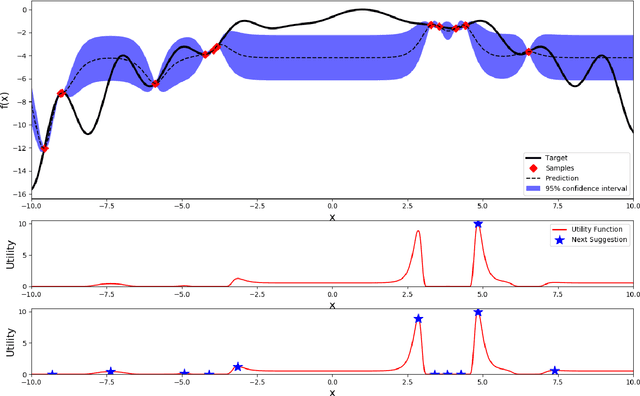
Most machine learning methods require careful selection of hyper-parameters in order to train a high performing model with good generalization abilities. Hence, several automatic selection algorithms have been introduced to overcome tedious manual (try and error) tuning of these parameters. Due to its very high sample efficiency, Bayesian Optimization over a Gaussian Processes modeling of the parameter space has become the method of choice. Unfortunately, this approach suffers from a cubic compute complexity due to underlying Cholesky factorization, which makes it very hard to be scaled beyond a small number of sampling steps. In this paper, we present a novel, highly accurate approximation of the underlying Gaussian Process. Reducing its computational complexity from cubic to quadratic allows an efficient strong scaling of Bayesian Optimization while outperforming the previous approach regarding optimization accuracy. The first experiments show speedups of a factor of 162 in single node and further speed up by a factor of 5 in a parallel environment.

GradVis: Visualization and Second Order Analysis of Optimization Surfaces during the Training of Deep Neural Networks

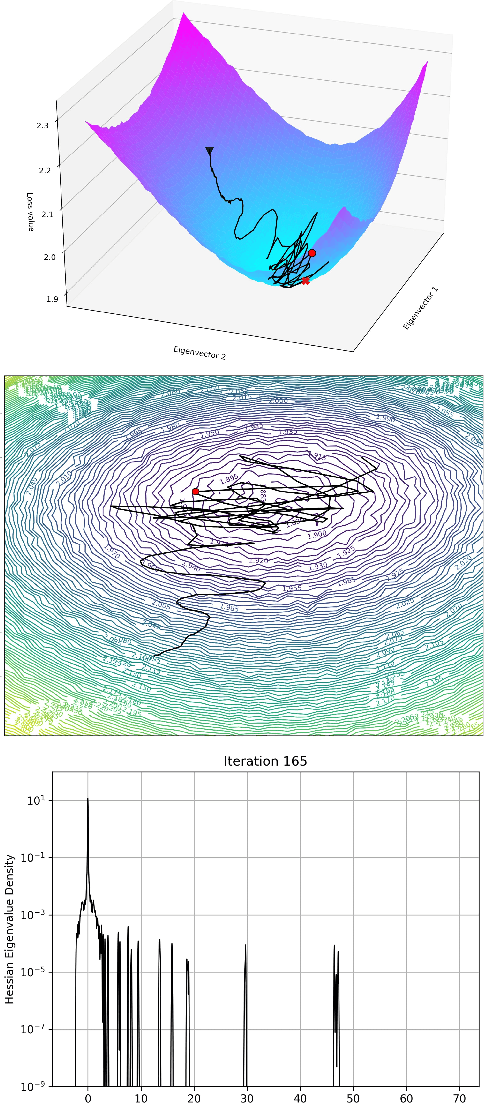
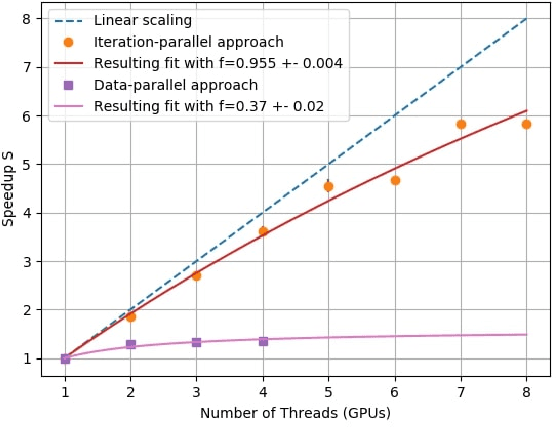
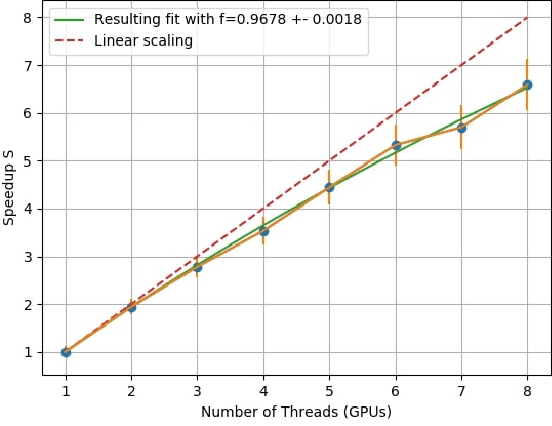
Current training methods for deep neural networks boil down to very high dimensional and non-convex optimization problems which are usually solved by a wide range of stochastic gradient descent methods. While these approaches tend to work in practice, there are still many gaps in the theoretical understanding of key aspects like convergence and generalization guarantees, which are induced by the properties of the optimization surface (loss landscape). In order to gain deeper insights, a number of recent publications proposed methods to visualize and analyze the optimization surfaces. However, the computational cost of these methods are very high, making it hardly possible to use them on larger networks. In this paper, we present the GradVis Toolbox, an open source library for efficient and scalable visualization and analysis of deep neural network loss landscapes in Tensorflow and PyTorch. Introducing more efficient mathematical formulations and a novel parallelization scheme, GradVis allows to plot 2d and 3d projections of optimization surfaces and trajectories, as well as high resolution second order gradient information for large networks.