Probabilistic Simplex Component Analysis by Importance Sampling

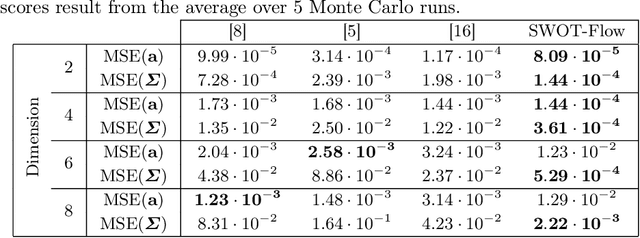
In this paper we consider the problem of linear unmixing hidden random variables defined over the simplex with additive Gaussian noise, also known as probabilistic simplex component analysis (PRISM). Previous solutions to tackle this challenging problem were based on geometrical approaches or computationally intensive variational methods. In contrast, we propose a conventional expectation maximization (EM) algorithm which embeds importance sampling. For this purpose, the proposal distribution is chosen as a simple surrogate distribution of the target posterior that is guaranteed to lie in the simplex. This distribution is based on the Gaussian linear minimum mean squared error (LMMSE) approximation which is accurate at high signal-to-noise ratio. Numerical experiments in different settings demonstrate the advantages of this adaptive surrogate over state-of-the-art methods.

Sliced-Wasserstein normalizing flows: beyond maximum likelihood training

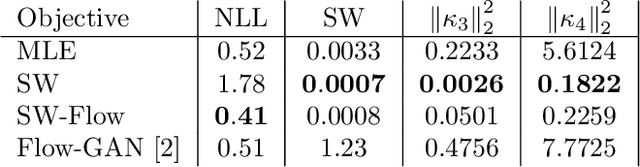
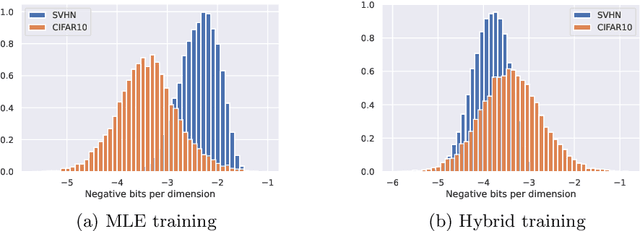
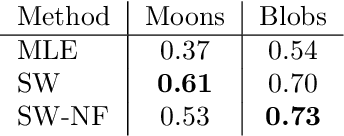
Despite their advantages, normalizing flows generally suffer from several shortcomings including their tendency to generate unrealistic data (e.g., images) and their failing to detect out-of-distribution data. One reason for these deficiencies lies in the training strategy which traditionally exploits a maximum likelihood principle only. This paper proposes a new training paradigm based on a hybrid objective function combining the maximum likelihood principle (MLE) and a sliced-Wasserstein distance. Results obtained on synthetic toy examples and real image data sets show better generative abilities in terms of both likelihood and visual aspects of the generated samples. Reciprocally, the proposed approach leads to a lower likelihood of out-of-distribution data, demonstrating a greater data fidelity of the resulting flows.

Learning Optimal Transport Between two Empirical Distributions with Normalizing Flows

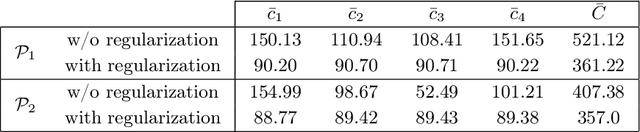
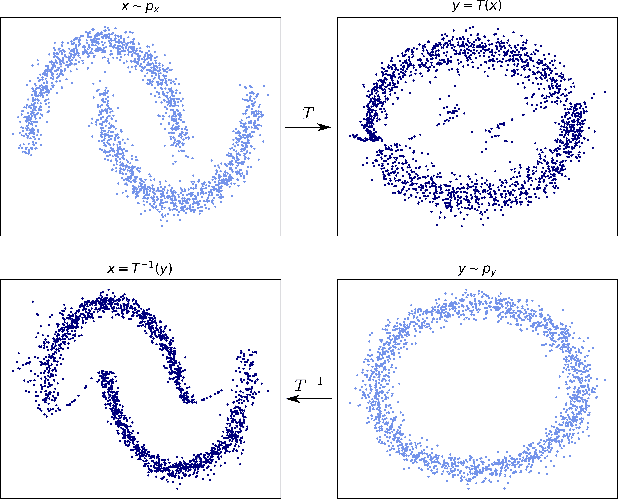
Optimal transport (OT) provides effective tools for comparing and mapping probability measures. We propose to leverage the flexibility of neural networks to learn an approximate optimal transport map. More precisely, we present a new and original method to address the problem of transporting a finite set of samples associated with a first underlying unknown distribution towards another finite set of samples drawn from another unknown distribution. We show that a particular instance of invertible neural networks, namely the normalizing flows, can be used to approximate the solution of this OT problem between a pair of empirical distributions. To this aim, we propose to relax the Monge formulation of OT by replacing the equality constraint on the push-forward measure by the minimization of the corresponding Wasserstein distance. The push-forward operator to be retrieved is then restricted to be a normalizing flow which is trained by optimizing the resulting cost function. This approach allows the transport map to be discretized as a composition of functions. Each of these functions is associated to one sub-flow of the network, whose output provides intermediate steps of the transport between the original and target measures. This discretization yields also a set of intermediate barycenters between the two measures of interest. Experiments conducted on toy examples as well as a challenging task of unsupervised translation demonstrate the interest of the proposed method. Finally, some experiments show that the proposed approach leads to a good approximation of the true OT.

CD-GAN: a robust fusion-based generative adversarial network for unsupervised change detection between heterogeneous images

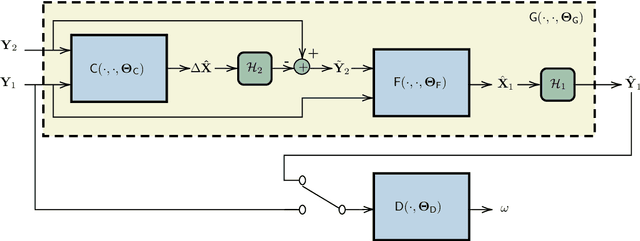
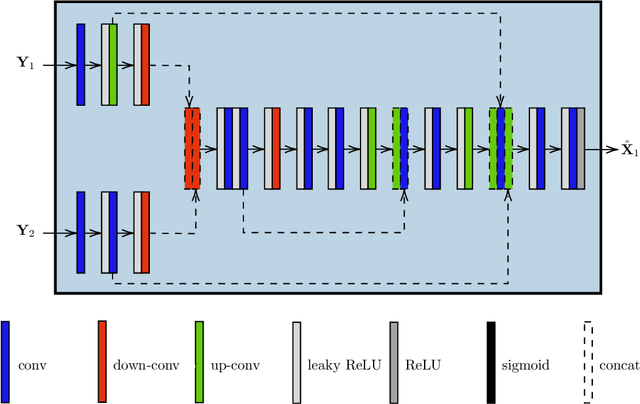
In the context of Earth observation, the detection of changes is performed from multitemporal images acquired by sensors with possibly different characteristics and modalities. Even when restricting to the optical modality, this task has proved to be challenging as soon as the sensors provide images of different spatial and/or spectral resolutions. This paper proposes a novel unsupervised change detection method dedicated to such so-called heterogeneous optical images. This method capitalizes on recent advances which frame the change detection problem into a robust fusion framework. More precisely, we show that a deep adversarial network designed and trained beforehand to fuse a pair of multiband images can be easily complemented by a network with the same architecture to perform change detection. The resulting overall architecture itself follows an adversarial strategy where the fusion network and the additional network are interpreted as essential building blocks of a generator. A comparison with state-of-the-art change detection methods demonstrate the versatility and the effectiveness of the proposed approach.

Provably robust blind source separation of linear-quadratic near-separable mixtures

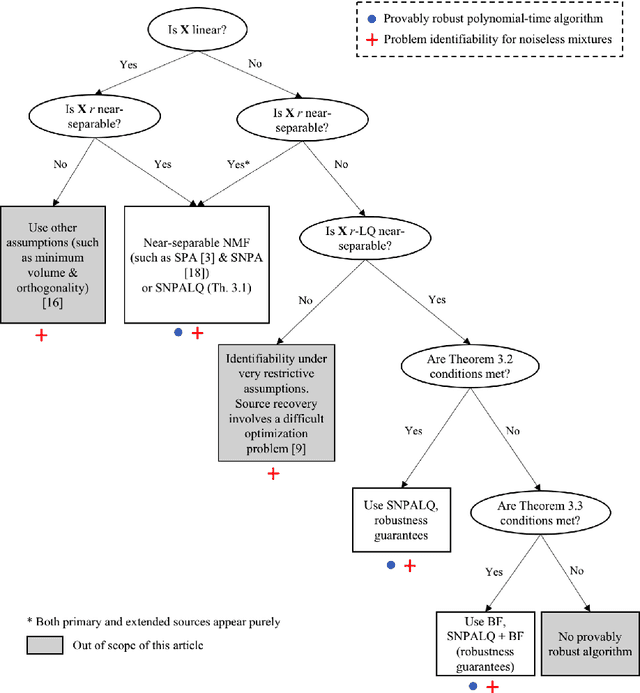
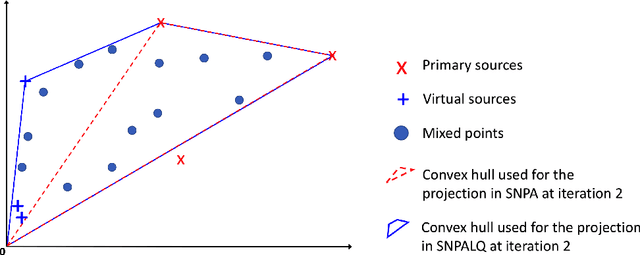
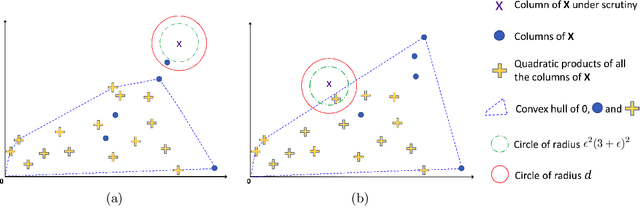
In this work, we consider the problem of blind source separation (BSS) by departing from the usual linear model and focusing on the linear-quadratic (LQ) model. We propose two provably robust and computationally tractable algorithms to tackle this problem under separability assumptions which require the sources to appear as samples in the data set. The first algorithm generalizes the successive nonnegative projection algorithm (SNPA), designed for linear BSS, and is referred to as SNPALQ. By explicitly modeling the product terms inherent to the LQ model along the iterations of the SNPA scheme, the nonlinear contributions of the mixing are mitigated, thus improving the separation quality. SNPALQ is shown to be able to recover the ground truth factors that generated the data, even in the presence of noise. The second algorithm is a brute-force (BF) algorithm, which is used as a post-processing step for SNPALQ. It enables to discard the spurious (mixed) samples extracted by SNPALQ, thus broadening its applicability. The BF is in turn shown to be robust to noise under easier-to-check and milder conditions than SNPALQ. We show that SNPALQ with and without the BF postprocessing is relevant in realistic numerical experiments.

Fast reconstruction of atomic-scale STEM-EELS images from sparse sampling

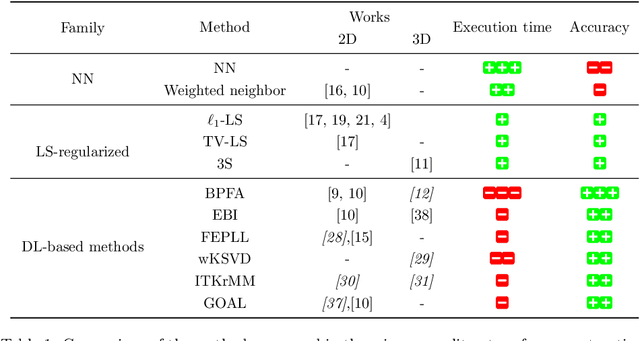
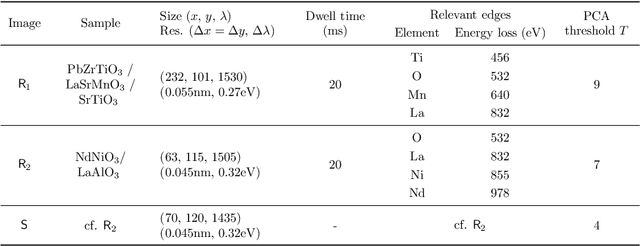
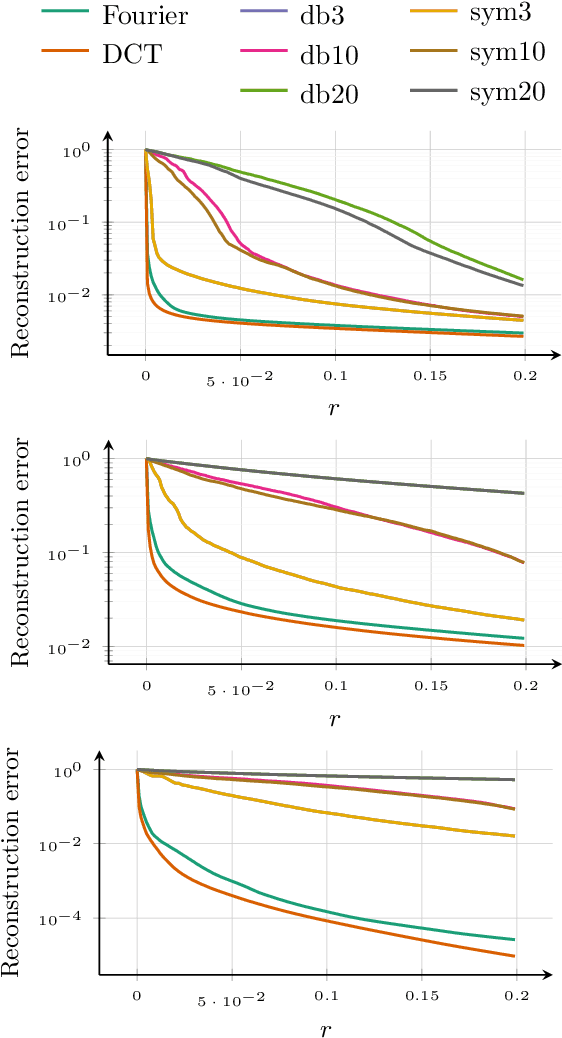
This paper discusses the reconstruction of partially sampled spectrum-images to accelerate the acquisition in scanning transmission electron microscopy (STEM). The problem of image reconstruction has been widely considered in the literature for many imaging modalities, but only a few attempts handled 3D data such as spectral images acquired by STEM electron energy loss spectroscopy (EELS). Besides, among the methods proposed in the microscopy literature, some are fast but inaccurate while others provide accurate reconstruction but at the price of a high computation burden. Thus none of the proposed reconstruction methods fulfills our expectations in terms of accuracy and computation complexity. In this paper, we propose a fast and accurate reconstruction method suited for atomic-scale EELS. This method is compared to popular solutions such as beta process factor analysis (BPFA) which is used for the first time on STEM-EELS images. Experiments based on real as synthetic data will be conducted.

Hyperspectral and multispectral image fusion under spectrally varying spatial blurs -- Application to high dimensional infrared astronomical imaging

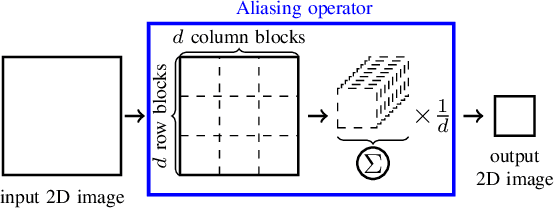
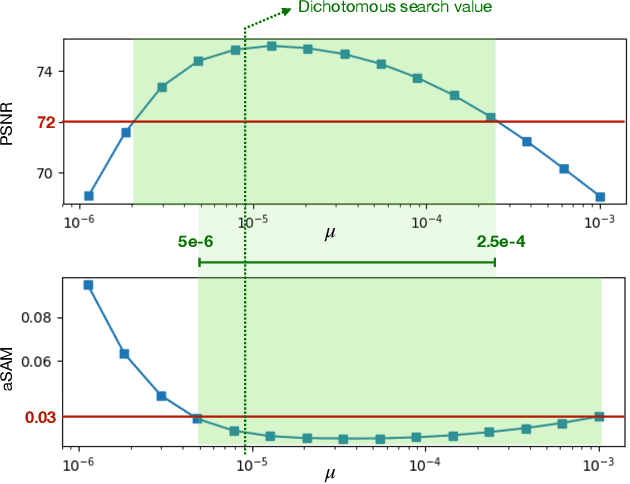
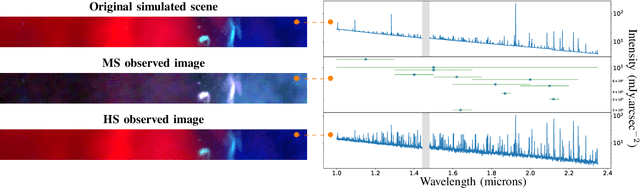
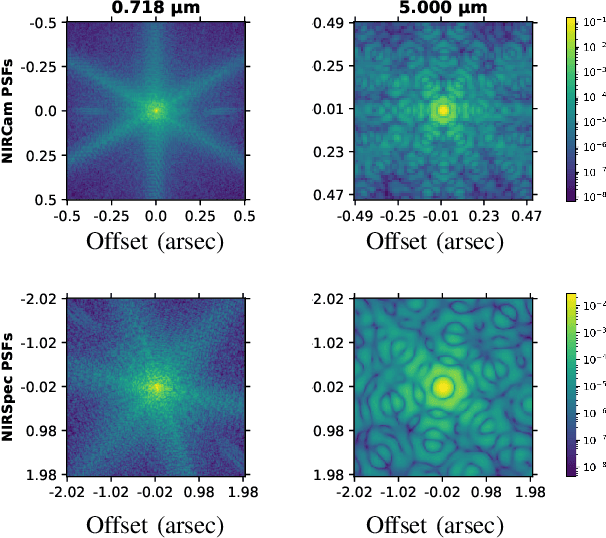
Hyperspectral imaging has become a significant source of valuable data for astronomers over the past decades. Current instrumental and observing time constraints allow direct acquisition of multispectral images, with high spatial but low spectral resolution, and hyperspectral images, with low spatial but high spectral resolution. To enhance scientific interpretation of the data, we propose a data fusion method which combines the benefits of each image to recover a high spatio-spectral resolution datacube. The proposed inverse problem accounts for the specificities of astronomical instruments, such as spectrally variant blurs. We provide a fast implementation by solving the problem in the frequency domain and in a low-dimensional subspace to efficiently handle the convolution operators as well as the high dimensionality of the data. We conduct experiments on a realistic synthetic dataset of simulated observation of the upcoming James Webb Space Telescope, and we show that our fusion algorithm outperforms state-of-the-art methods commonly used in remote sensing for Earth observation.

Matrix cofactorization for joint spatial-spectral unmixing of hyperspectral images

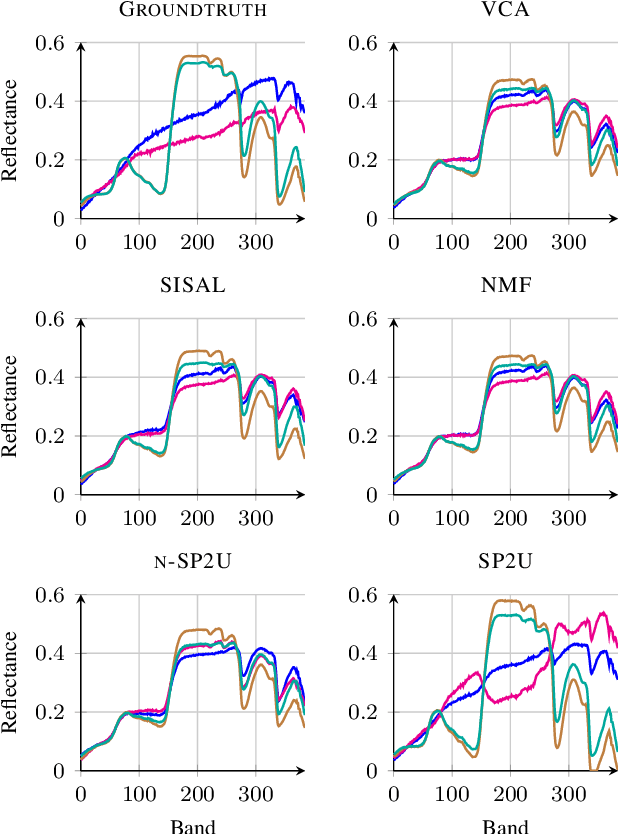
Hyperspectral unmixing aims at identifying a set of elementary spectra and the corresponding mixture coefficients for each pixel of an image. As the elementary spectra correspond to the reflectance spectra of real materials, they are often very correlated yielding an ill-conditioned problem. To enrich the model and to reduce ambiguity due to the high correlation, it is common to introduce spatial information to complement the spectral information. The most common way to introduce spatial information is to rely on a spatial regularization of the abundance maps. In this paper, instead of considering a simple but limited regularization process, spatial information is directly incorporated through the newly proposed context of spatial unmixing. Contextual features are extracted for each pixel and this additional set of observations is decomposed according to a linear model. Finally the spatial and spectral observations are unmixed jointly through a cofactorization model. In particular, this model introduces a coupling term used to identify clusters of shared spatial and spectral signatures. An evaluation of the proposed method is conducted on synthetic and real data and shows that results are accurate and also very meaningful since they describe both spatially and spectrally the various areas of the scene.

Asymptotically exact data augmentation: models, properties and algorithms

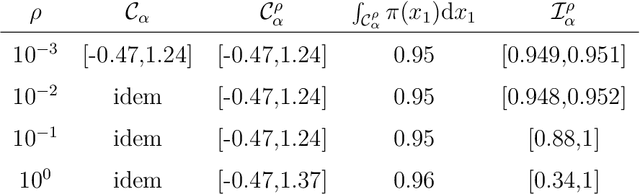
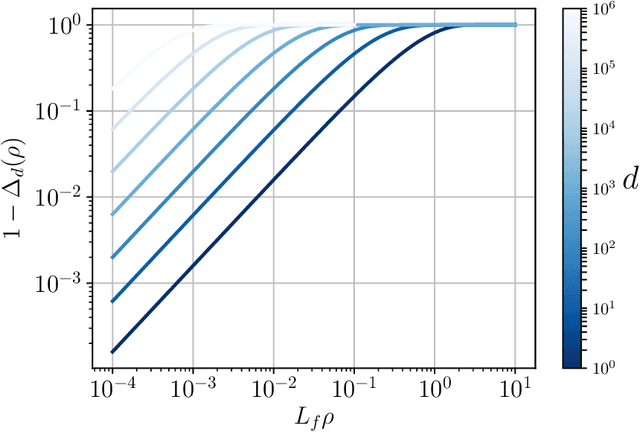
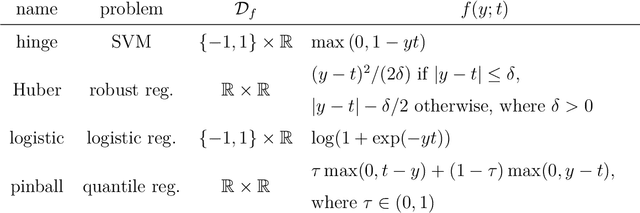
Data augmentation, by the introduction of auxiliary variables, has become an ubiquitous technique to improve mixing/convergence properties, simplify the implementation or reduce the computational time of inference methods such as Markov chain Monte Carlo. Nonetheless, introducing appropriate auxiliary variables while preserving the initial target probability distribution cannot be conducted in a systematic way but highly depends on the considered problem. To deal with such issues, this paper draws a unified framework, namely asymptotically exact data augmentation (AXDA), which encompasses several well-established but also more recent approximate augmented models. Benefiting from a much more general perspective, it delivers some additional qualitative and quantitative insights concerning these schemes. In particular, general properties of AXDA along with non-asymptotic theoretical results on the approximation that is made are stated. Close connections to existing Bayesian methods (e.g. mixture modeling, robust Bayesian models and approximate Bayesian computation) are also drawn. All the results are illustrated with examples and applied to standard statistical learning problems.

Matrix Cofactorization for Joint Representation Learning and Supervised Classification -- Application to Hyperspectral Image Analysis

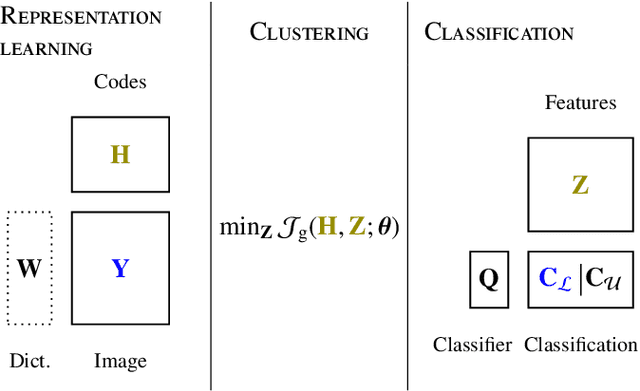
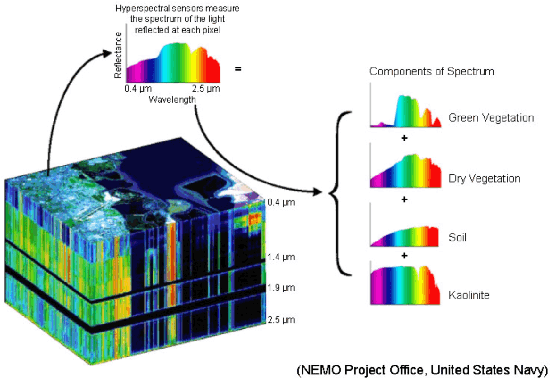
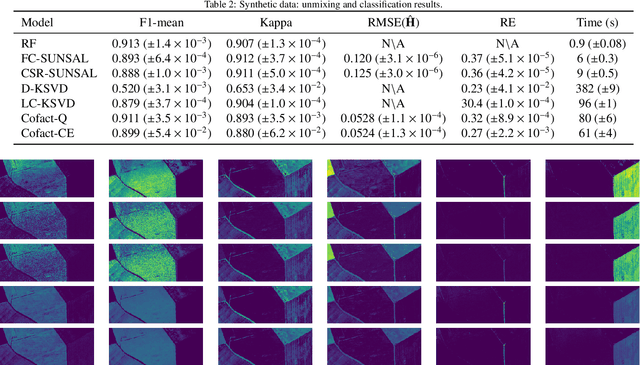
Supervised classification and representation learning are two widely used methods to analyze multivariate images. Although complementary, these two classes of methods have been scarcely considered jointly. In this paper, a method coupling these two approaches is designed using a matrix cofactorization formulation. Each task is modeled as a factorization matrix problem and a term relating both coding matrices is then introduced to drive an appropriate coupling. The link can be interpreted as a clustering operation over the low-dimensional representation vectors. The attribution vectors of the clustering are then used as features vectors for the classification task, i.e., the coding vectors of the corresponding factorization problem. A proximal gradient descent algorithm, ensuring convergence to a critical point of the objective function, is then derived to solve the resulting non-convex non-smooth optimization problem. An evaluation of the proposed method is finally conducted both on synthetic and real data in the specific context of hyperspectral image interpretation, unifying two standard analysis techniques, namely unmixing and classification.