Subspace Detours Meet Gromov-Wasserstein

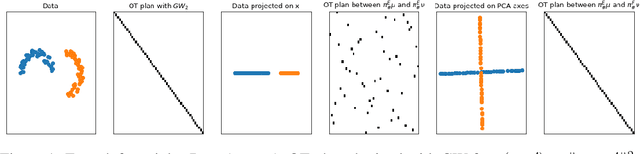
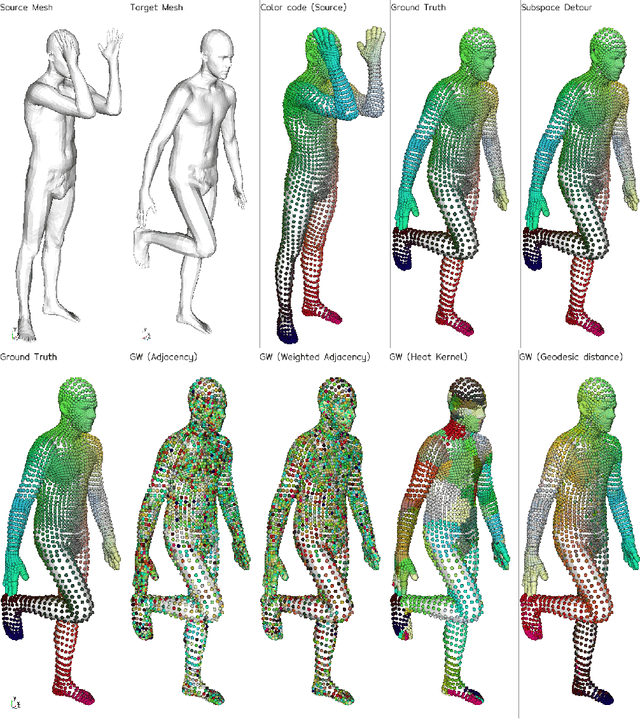
In the context of optimal transport methods, the subspace detour approach was recently presented by Muzellec and Cuturi (2019). It consists in building a nearly optimal transport plan in the measures space from an optimal transport plan in a wisely chosen subspace, onto which the original measures are projected. The contribution of this paper is to extend this category of methods to the Gromov-Wasserstein problem, which is a particular type of transport distance involving the inner geometry of the compared distributions. After deriving the associated formalism and properties, we also discuss a specific cost for which we can show connections with the Knothe-Rosenblatt rearrangement. We finally give an experimental illustration on a shape matching problem.

Factored couplings in multi-marginal optimal transport via difference of convex programming

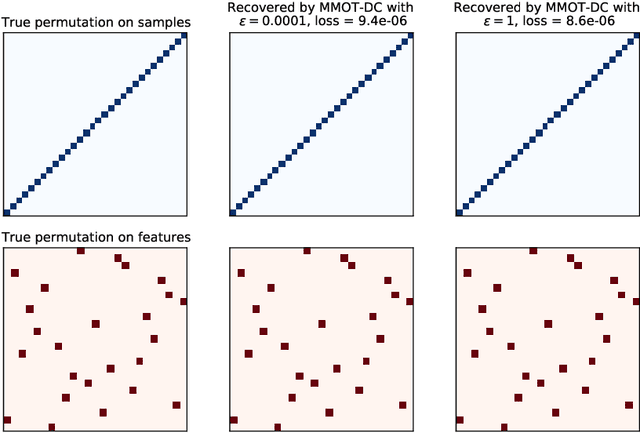
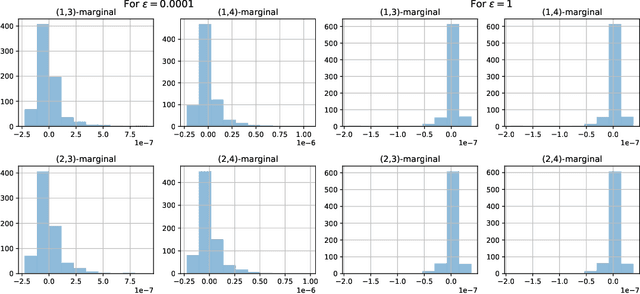
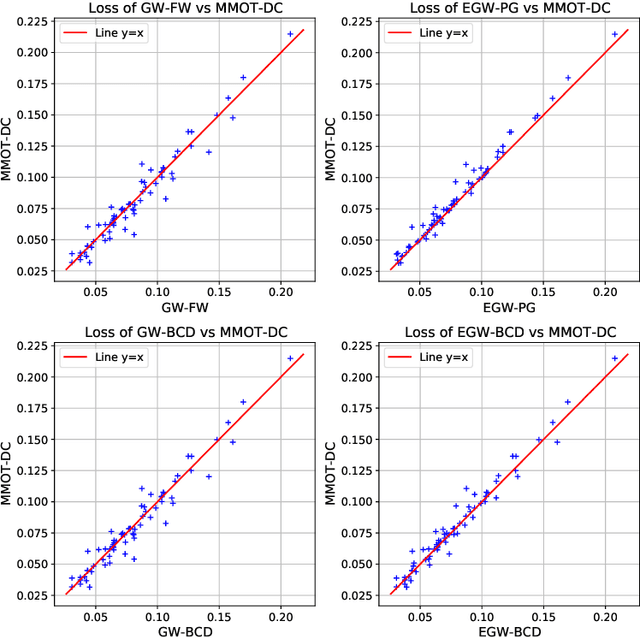
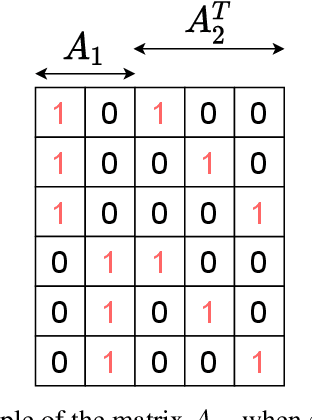
Optimal transport (OT) theory underlies many emerging machine learning (ML) methods nowadays solving a wide range of tasks such as generative modeling, transfer learning and information retrieval. These latter works, however, usually build upon a traditional OT setup with two distributions, while leaving a more general multi-marginal OT formulation somewhat unexplored. In this paper, we study the multi-marginal OT (MMOT) problem and unify several popular OT methods under its umbrella by promoting structural information on the coupling. We show that incorporating such structural information into MMOT results in an instance of a different of convex (DC) programming problem allowing us to solve it numerically. Despite high computational cost of the latter procedure, the solutions provided by DC optimization are usually as qualitative as those obtained using currently employed optimization schemes.

Semi-relaxed Gromov Wasserstein divergence with applications on graphs

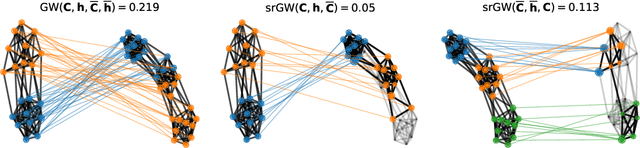
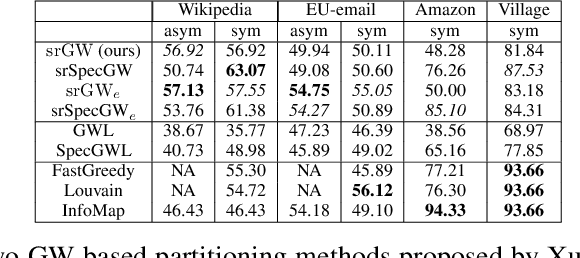
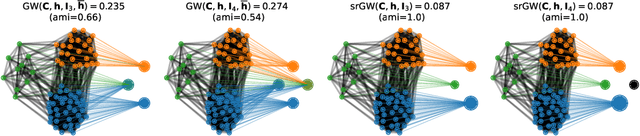
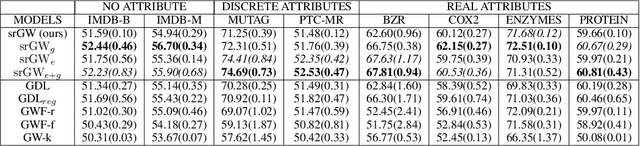
Comparing structured objects such as graphs is a fundamental operation involved in many learning tasks. To this end, the Gromov-Wasserstein (GW) distance, based on Optimal Transport (OT), has proven to be successful in handling the specific nature of the associated objects. More specifically, through the nodes connectivity relations, GW operates on graphs, seen as probability measures over specific spaces. At the core of OT is the idea of conservation of mass, which imposes a coupling between all the nodes from the two considered graphs. We argue in this paper that this property can be detrimental for tasks such as graph dictionary or partition learning, and we relax it by proposing a new semi-relaxed Gromov-Wasserstein divergence. Aside from immediate computational benefits, we discuss its properties, and show that it can lead to an efficient graph dictionary learning algorithm. We empirically demonstrate its relevance for complex tasks on graphs such as partitioning, clustering and completion.

Unbalanced minibatch Optimal Transport; applications to Domain Adaptation

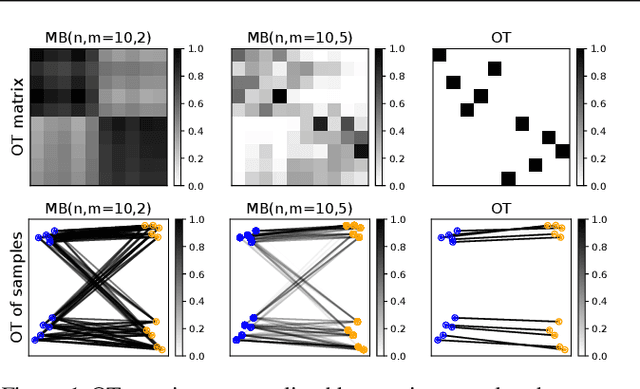
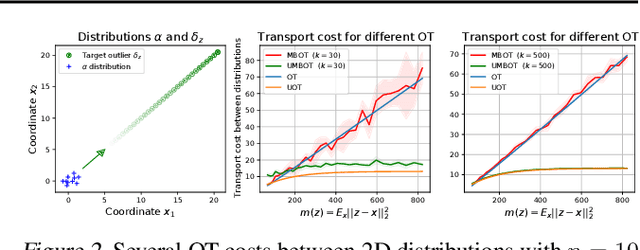
Optimal transport distances have found many applications in machine learning for their capacity to compare non-parametric probability distributions. Yet their algorithmic complexity generally prevents their direct use on large scale datasets. Among the possible strategies to alleviate this issue, practitioners can rely on computing estimates of these distances over subsets of data, {\em i.e.} minibatches. While computationally appealing, we highlight in this paper some limits of this strategy, arguing it can lead to undesirable smoothing effects. As an alternative, we suggest that the same minibatch strategy coupled with unbalanced optimal transport can yield more robust behavior. We discuss the associated theoretical properties, such as unbiased estimators, existence of gradients and concentration bounds. Our experimental study shows that in challenging problems associated to domain adaptation, the use of unbalanced optimal transport leads to significantly better results, competing with or surpassing recent baselines.

Learning to Generate Wasserstein Barycenters

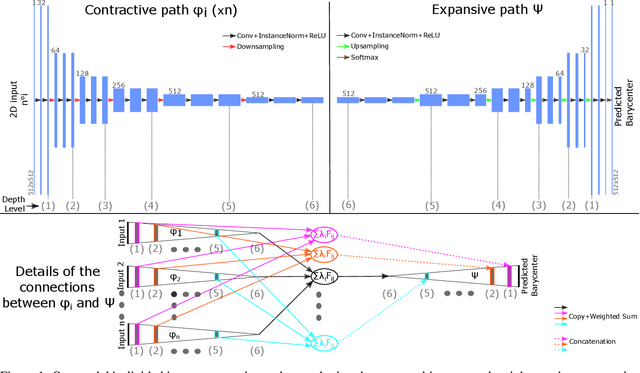
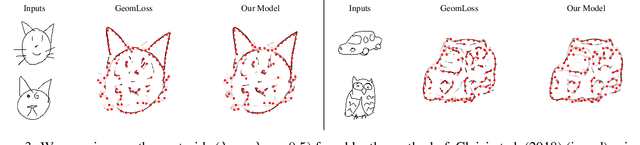
Optimal transport is a notoriously difficult problem to solve numerically, with current approaches often remaining intractable for very large scale applications such as those encountered in machine learning. Wasserstein barycenters -- the problem of finding measures in-between given input measures in the optimal transport sense -- is even more computationally demanding as it requires to solve an optimization problem involving optimal transport distances. By training a deep convolutional neural network, we improve by a factor of 60 the computational speed of Wasserstein barycenters over the fastest state-of-the-art approach on the GPU, resulting in milliseconds computational times on $512\times512$ regular grids. We show that our network, trained on Wasserstein barycenters of pairs of measures, generalizes well to the problem of finding Wasserstein barycenters of more than two measures. We demonstrate the efficiency of our approach for computing barycenters of sketches and transferring colors between multiple images.

Online Graph Dictionary Learning

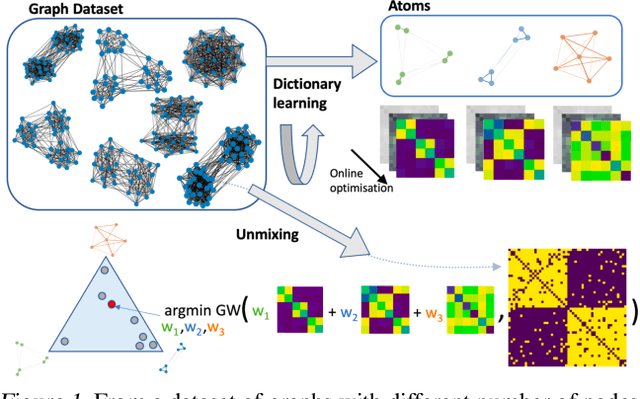
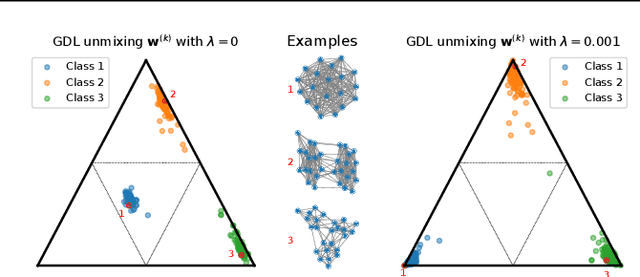
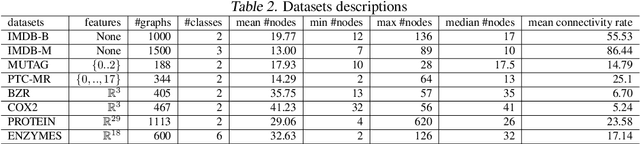
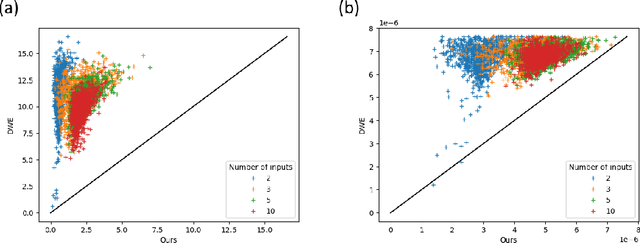
Dictionary learning is a key tool for representation learning, that explains the data as linear combination of few basic elements. Yet, this analysis is not amenable in the context of graph learning, as graphs usually belong to different metric spaces. We fill this gap by proposing a new online Graph Dictionary Learning approach, which uses the Gromov Wasserstein divergence for the data fitting term. In our work, graphs are encoded through their nodes' pairwise relations and modeled as convex combination of graph atoms, i.e. dictionary elements, estimated thanks to an online stochastic algorithm, which operates on a dataset of unregistered graphs with potentially different number of nodes. Our approach naturally extends to labeled graphs, and is completed by a novel upper bound that can be used as a fast approximation of Gromov Wasserstein in the embedding space. We provide numerical evidences showing the interest of our approach for unsupervised embedding of graph datasets and for online graph subspace estimation and tracking.

Minibatch optimal transport distances; analysis and applications

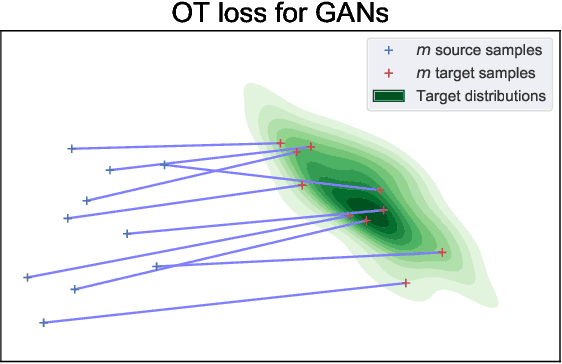
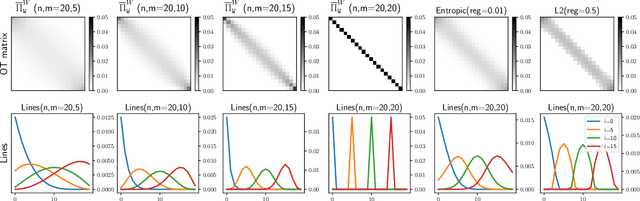
Optimal transport distances have become a classic tool to compare probability distributions and have found many applications in machine learning. Yet, despite recent algorithmic developments, their complexity prevents their direct use on large scale datasets. To overcome this challenge, a common workaround is to compute these distances on minibatches i.e. to average the outcome of several smaller optimal transport problems. We propose in this paper an extended analysis of this practice, which effects were previously studied in restricted cases. We first consider a large variety of Optimal Transport kernels. We notably argue that the minibatch strategy comes with appealing properties such as unbiased estimators, gradients and a concentration bound around the expectation, but also with limits: the minibatch OT is not a distance. To recover some of the lost distance axioms, we introduce a debiased minibatch OT function and study its statistical and optimisation properties. Along with this theoretical analysis, we also conduct empirical experiments on gradient flows, generative adversarial networks (GANs) or color transfer that highlight the practical interest of this strategy.

Contextual Semantic Interpretability

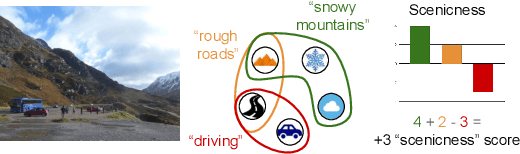
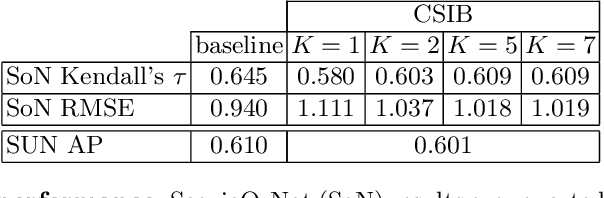
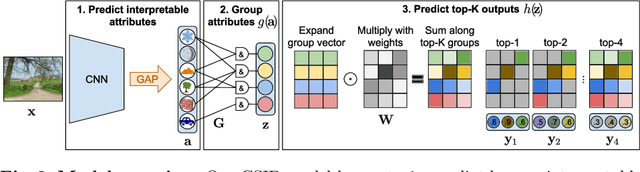
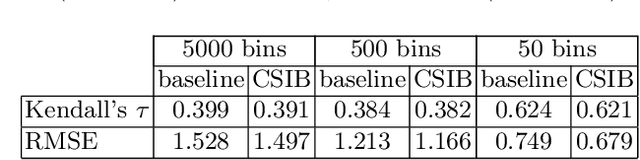
Convolutional neural networks (CNN) are known to learn an image representation that captures concepts relevant to the task, but do so in an implicit way that hampers model interpretability. However, one could argue that such a representation is hidden in the neurons and can be made explicit by teaching the model to recognize semantically interpretable attributes that are present in the scene. We call such an intermediate layer a \emph{semantic bottleneck}. Once the attributes are learned, they can be re-combined to reach the final decision and provide both an accurate prediction and an explicit reasoning behind the CNN decision. In this paper, we look into semantic bottlenecks that capture context: we want attributes to be in groups of a few meaningful elements and participate jointly to the final decision. We use a two-layer semantic bottleneck that gathers attributes into interpretable, sparse groups, allowing them contribute differently to the final output depending on the context. We test our contextual semantic interpretable bottleneck (CSIB) on the task of landscape scenicness estimation and train the semantic interpretable bottleneck using an auxiliary database (SUN Attributes). Our model yields in predictions as accurate as a non-interpretable baseline when applied to a real-world test set of Flickr images, all while providing clear and interpretable explanations for each prediction.

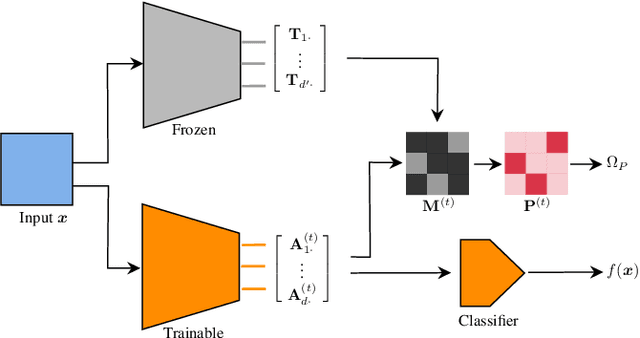
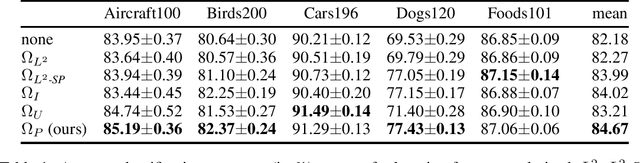
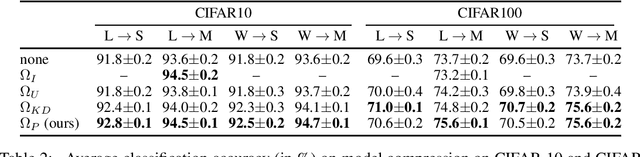
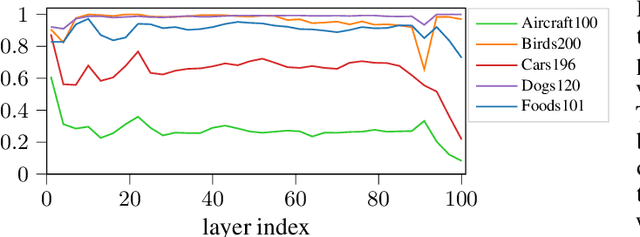
Representation Transfer by Optimal Transport

Deep learning currently provides the best representations of complex objects for a wide variety of tasks. However, learning these representations is an expensive process that requires very large training samples and significant computing resources. Thankfully, sharing these representations is a common practice, enabling to solve new tasks with relatively little training data and few computing resources; the transfer of representations is nowadays an essential ingredient in numerous real-world applications of deep learning. Transferring representations commonly relies on the parameterized form of the features making up the representation, as encoded by the computational graph of these features. In this paper, we propose to use a novel non-parametric metric between representations. It is based on a functional view of features, and takes into account certain invariances of representations, such as the permutation of their features, by relying on optimal transport. This distance is used as a regularization term promoting similarity between two representations. We show the relevance of this approach in two representation transfer settings, where the representation of a trained reference model is transferred to another one, for solving a new related task (inductive transfer learning), or for distilling knowledge to a simpler model (model compression).

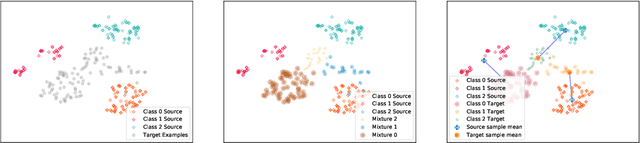
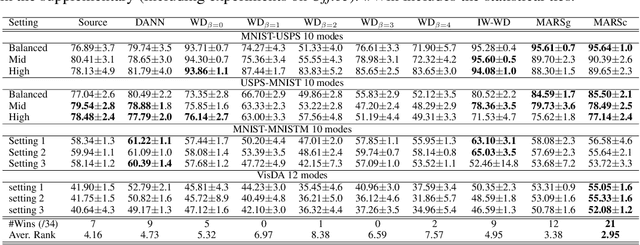
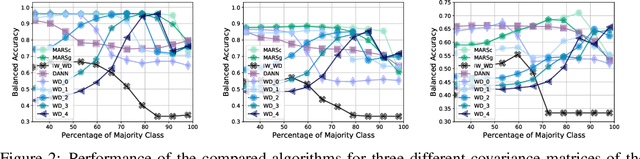
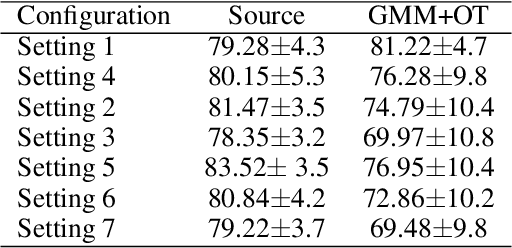
Match and Reweight Strategy for Generalized Target Shift

We address the problem of unsupervised domain adaptation under the setting of generalized target shift (both class-conditional and label shifts occur). We show that in that setting, for good generalization, it is necessary to learn with similar source and target label distributions and to match the class-conditional probabilities. For this purpose, we propose an estimation of target label proportion by blending mixture estimation and optimal transport. This estimation comes with theoretical guarantees of correctness. Based on the estimation, we learn a model by minimizing a importance weighted loss and a Wasserstein distance between weighted marginals. We prove that this minimization allows to match class-conditionals given mild assumptions on their geometry. Our experimental results show that our method performs better on average than competitors accross a range domain adaptation problems including digits,VisDA and Office.