Quantum Doubly Stochastic Transformers

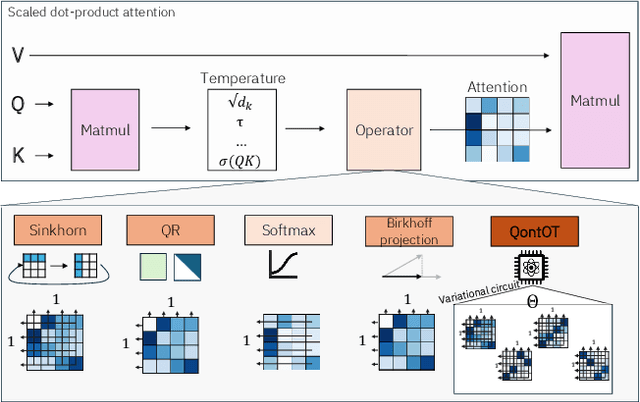
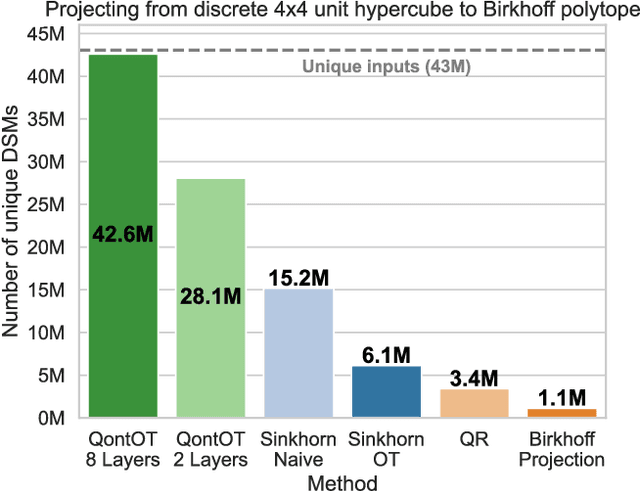
At the core of the Transformer, the Softmax normalizes the attention matrix to be right stochastic. Previous research has shown that this often destabilizes training and that enforcing the attention matrix to be doubly stochastic (through Sinkhorn's algorithm) consistently improves performance across different tasks, domains and Transformer flavors. However, Sinkhorn's algorithm is iterative, approximative, non-parametric and thus inflexible w.r.t. the obtained doubly stochastic matrix (DSM). Recently, it has been proven that DSMs can be obtained with a parametric quantum circuit, yielding a novel quantum inductive bias for DSMs with no known classical analogue. Motivated by this, we demonstrate the feasibility of a hybrid classical-quantum doubly stochastic Transformer (QDSFormer) that replaces the Softmax in the self-attention layer with a variational quantum circuit. We study the expressive power of the circuit and find that it yields more diverse DSMs that better preserve information than classical operators. Across multiple small-scale object recognition tasks, we find that our QDSFormer consistently surpasses both a standard Vision Transformer and other doubly stochastic Transformers. Beyond the established Sinkformer, this comparison includes a novel quantum-inspired doubly stochastic Transformer (based on QR decomposition) that can be of independent interest. The QDSFormer also shows improved training stability and lower performance variation suggesting that it may mitigate the notoriously unstable training of ViTs on small-scale data.

Black-box Uncertainty Quantification Method for LLM-as-a-Judge

LLM-as-a-Judge is a widely used method for evaluating the performance of Large Language Models (LLMs) across various tasks. We address the challenge of quantifying the uncertainty of LLM-as-a-Judge evaluations. While uncertainty quantification has been well-studied in other domains, applying it effectively to LLMs poses unique challenges due to their complex decision-making capabilities and computational demands. In this paper, we introduce a novel method for quantifying uncertainty designed to enhance the trustworthiness of LLM-as-a-Judge evaluations. The method quantifies uncertainty by analyzing the relationships between generated assessments and possible ratings. By cross-evaluating these relationships and constructing a confusion matrix based on token probabilities, the method derives labels of high or low uncertainty. We evaluate our method across multiple benchmarks, demonstrating a strong correlation between the accuracy of LLM evaluations and the derived uncertainty scores. Our findings suggest that this method can significantly improve the reliability and consistency of LLM-as-a-Judge evaluations.