Approaching I/O-optimality for Approximate Attention

We revisit the I/O complexity of attention in large language models. Given query-key-value matrices $Q,K,V\in\mathbb{R}^{n\times d}$, and a machine with fast memory size $M$, the goal is to compute the "attention matrix" $A=\text{softmax}(Q K ^{\top}/\sqrt{d}) V$ with the minimal number of data transfers between fast and slow memory. Existing methods in the literature, most notably FlashAttention and its variants, incur an I/O cost that depends quadratically on $n$, while a trivial lower bound only requires $Ω(nd)$ I/O's to read the inputs and write the output. In this work, we present a technique for computing attention where the I/O cost only depends almost-linearly on $n$ in most parameter regimes. This is achieved by developing I/O-efficient algorithms inspired by the recent approximate attention framework of Alman and Song. We also prove corresponding lower bounds in each parameter regime to show that our algorithms are indeed close to I/O-optimal.

Fast and Stable Triangular Inversion for Delta-Rule Linear Transformers

Linear attention has emerged as a cornerstone for efficient long-context architectures, as evidenced by its integration into state-of-the-art open-source models including Qwen3.5/3.6, Kimi Linear, and RWKV-7. Models that incorporate linear attention layers with the so-called Delta-Rule involve the inversion of triangular matrices as a core sub-routine. This operation often forms a performance bottleneck, and, due to its high-sensitivity to numerical errors, it can significantly deteriorate end-to-end model accuracy if it is not carefully implemented. This work provides a systematic analysis of both direct and iterative triangular inversion algorithms, targeting methods that are rich in matrix products, and, therefore, have the potential to efficiently utilize modern hardware. To that end, our analysis covers a broad spectrum of mathematical and practical aspects, with a heavy focus on numerical stability, computational complexity, and, ultimately, hardware efficiency and practical considerations. We provide a rigorous experimental evaluation to verify these properties in practical scenarios, and in low-precision floating-point representations, highlighting the strengths and limitations of each method. Performance benchmarks on NPUs reveal up to $4.3\times$ speed-up against the state-of-the-art implementations of SGLang for triangular matrix inversion, leading to significant performance improvements on the entire layer level, while maintaining full end-to-end model accuracy.

Quantum Doubly Stochastic Transformers

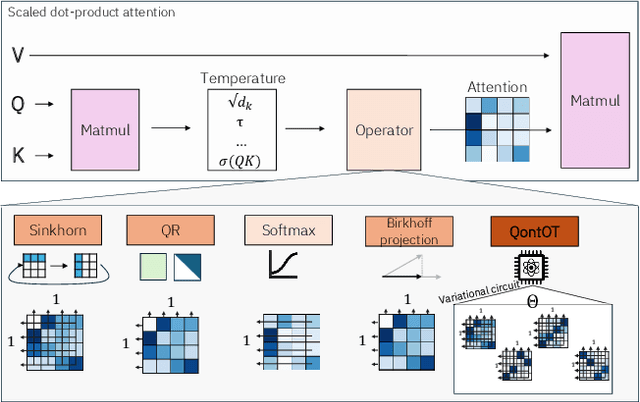
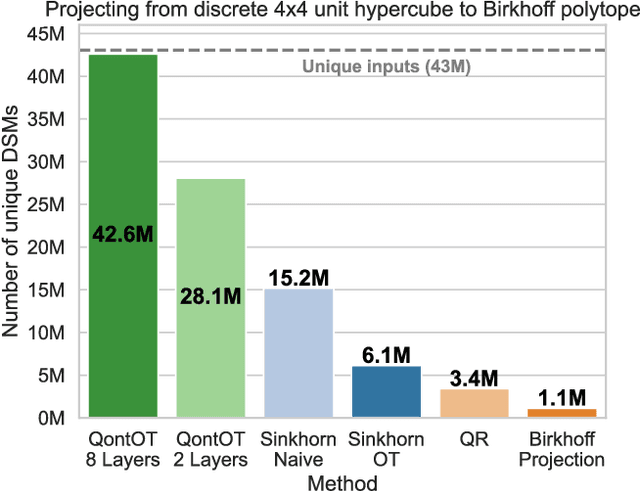
At the core of the Transformer, the Softmax normalizes the attention matrix to be right stochastic. Previous research has shown that this often destabilizes training and that enforcing the attention matrix to be doubly stochastic (through Sinkhorn's algorithm) consistently improves performance across different tasks, domains and Transformer flavors. However, Sinkhorn's algorithm is iterative, approximative, non-parametric and thus inflexible w.r.t. the obtained doubly stochastic matrix (DSM). Recently, it has been proven that DSMs can be obtained with a parametric quantum circuit, yielding a novel quantum inductive bias for DSMs with no known classical analogue. Motivated by this, we demonstrate the feasibility of a hybrid classical-quantum doubly stochastic Transformer (QDSFormer) that replaces the Softmax in the self-attention layer with a variational quantum circuit. We study the expressive power of the circuit and find that it yields more diverse DSMs that better preserve information than classical operators. Across multiple small-scale object recognition tasks, we find that our QDSFormer consistently surpasses both a standard Vision Transformer and other doubly stochastic Transformers. Beyond the established Sinkformer, this comparison includes a novel quantum-inspired doubly stochastic Transformer (based on QR decomposition) that can be of independent interest. The QDSFormer also shows improved training stability and lower performance variation suggesting that it may mitigate the notoriously unstable training of ViTs on small-scale data.

Estimating leverage scores via rank revealing methods and randomization

We study algorithms for estimating the statistical leverage scores of rectangular dense or sparse matrices of arbitrary rank. Our approach is based on combining rank revealing methods with compositions of dense and sparse randomized dimensionality reduction transforms. We first develop a set of fast novel algorithms for rank estimation, column subset selection and least squares preconditioning. We then describe the design and implementation of leverage score estimators based on these primitives. These estimators are also effective for rank deficient input, which is frequently the case in data analytics applications. We provide detailed complexity analyses for all algorithms as well as meaningful approximation bounds and comparisons with the state-of-the-art. We conduct extensive numerical experiments to evaluate our algorithms and to illustrate their properties and performance using synthetic and real world data sets.