Enhanced Prediction of CAR T-Cell Cytotoxicity with Quantum-Kernel Methods

Chimeric antigen receptor (CAR) T-cells are T-cells engineered to recognize and kill specific tumor cells. Through their extracellular domains, CAR T-cells bind tumor cell antigens which triggers CAR T activation and proliferation. These processes are regulated by co-stimulatory domains present in the intracellular region of the CAR T-cell. Through integrating novel signaling components into the co-stimulatory domains, it is possible to modify CAR T-cell phenotype. Identifying and experimentally testing new CAR constructs based on libraries of co-stimulatory domains is nontrivial given the vast combinatorial space defined by such libraries. This leads to a highly data constrained, poorly explored combinatorial problem, where the experiments undersample all possible combinations. We propose a quantum approach using a Projected Quantum Kernel (PQK) to address this challenge. PQK operates by embedding classical data into a high dimensional Hilbert space and employs a kernel method to measure sample similarity. Using 61 qubits on a gate-based quantum computer, we demonstrate the largest PQK application to date and an enhancement in the classification performance over purely classical machine learning methods for CAR T cytotoxicity prediction. Importantly, we show improved learning for specific signaling domains and domain positions, particularly where there was lower information highlighting the potential for quantum computing in data-constrained problems.

Quantum Doubly Stochastic Transformers

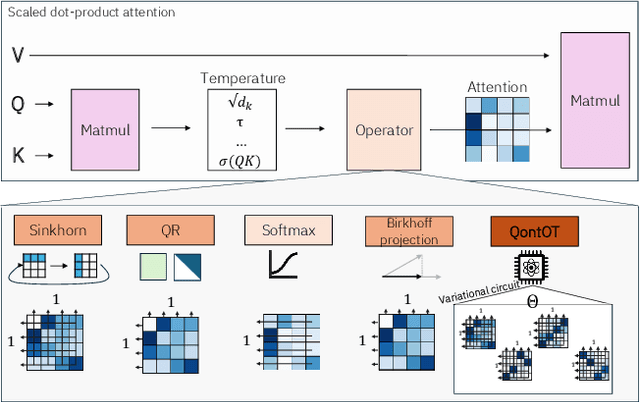
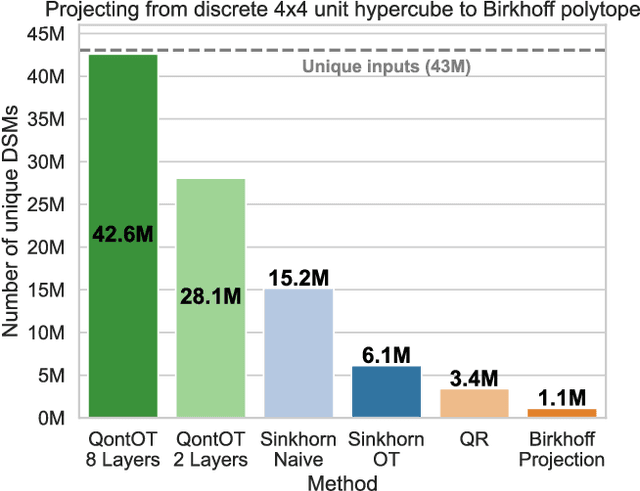
At the core of the Transformer, the Softmax normalizes the attention matrix to be right stochastic. Previous research has shown that this often destabilizes training and that enforcing the attention matrix to be doubly stochastic (through Sinkhorn's algorithm) consistently improves performance across different tasks, domains and Transformer flavors. However, Sinkhorn's algorithm is iterative, approximative, non-parametric and thus inflexible w.r.t. the obtained doubly stochastic matrix (DSM). Recently, it has been proven that DSMs can be obtained with a parametric quantum circuit, yielding a novel quantum inductive bias for DSMs with no known classical analogue. Motivated by this, we demonstrate the feasibility of a hybrid classical-quantum doubly stochastic Transformer (QDSFormer) that replaces the Softmax in the self-attention layer with a variational quantum circuit. We study the expressive power of the circuit and find that it yields more diverse DSMs that better preserve information than classical operators. Across multiple small-scale object recognition tasks, we find that our QDSFormer consistently surpasses both a standard Vision Transformer and other doubly stochastic Transformers. Beyond the established Sinkformer, this comparison includes a novel quantum-inspired doubly stochastic Transformer (based on QR decomposition) that can be of independent interest. The QDSFormer also shows improved training stability and lower performance variation suggesting that it may mitigate the notoriously unstable training of ViTs on small-scale data.